题目描述
如题,给出一个(N)次函数,保证在范围([l,r])内存在一点(x),使得([l,x])上单调增,([x,r])上单调减。试求出(x)的值。
输入输出格式
输入格式:
第一行一次包含一个正整数(N)和两个实数(l、r),含义如题目描述所示。
第二行包含(N+1)个实数,从高到低依次表示该(N)次函数各项的系数。
输出格式:
输出为一行,包含一个实数,即为(x)的值。四舍五入保留(5)位小数。
输入输出样例
输入样例#1:
3 -0.9981 0.5
1 -3 -3 1
输出样例#1:
-0.41421
说明
时空限制:(50ms,128M)
数据规模:
对于(100\%)的数据:(7<=N<=13)
样例说明:
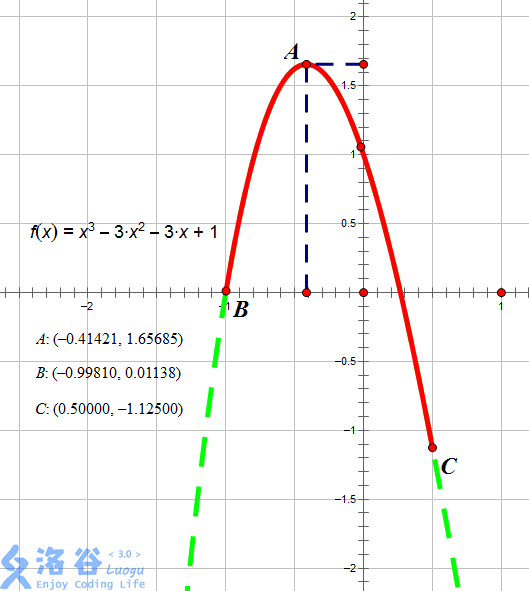
如图所示,红色段即为该函数(f(x)=x^3-3x^2-3x+1)在区间([-0.9981,0.5])上的图像。
当(x=-0.41421)时图像位于最高点,故此时函数在([l,x])上单调增,([x,r])上单调减,故(x=-0.41421),输出(-0.41421)。
(Tip.l&r(的范围并不是非常大)ww$不会超过一位数)
思路:其实之前做过这个题目,但是用的不是三分法,所以今天看知识体系,刚好发现自己不会三分法,就去学习了一下顺便回顾了这道模板题,三分的思路就是,先取(l)和(r)的中间点(mid),再取(mid)和(r)的中间值(mmid),然后比较(f(mid))和(f(mmid)),其中(f(x))表示把x代入函数后的值为多少,如果(f(mid)>f(mmid)),说明要找的点在(mmid)的左边,所以就让(r=mmid),继续三分,反之,让(l=mid),继续三分,最后的(l)和(r)一定会越来越接近要找的点,r和l的差在误差允许范围内时,就找完了。
代码:
#include<cstdio>
#include<algorithm>
#define dl double
#define maxn 15
using namespace std;
const dl eps=1e-7;
int n;
dl a[maxn],l,r,p;
inline dl js(dl x) {
dl res=a[0];
for(int i=1;i<=n;++i) {
dl tmp=a[i];
for(int j=1;j<=i;++j)
tmp*=x;
res+=tmp;
}
return res;
}
int main() {
scanf("%d%lf%lf",&n,&l,&r);
for(int i=n;i>=0;--i) {
scanf("%lf",&p);
a[i]=p;
}
while(l+eps<r) {
dl mid=(l+r)/2;
dl mmid=(mid+r)/2;
if(js(mid)>js(mmid)) r=mmid;
else l=mid;
}
dl ans=js(l)>js(r)?l:r;
printf("%0.5lf
",r);
return 0;
}