Description:
一棵树是一个简单无向图,图中任意两个节点仅被一条边连接,所有连通无环无向图都是一棵树。(-Wikipedia)
最近公共祖先((LCA))是……(此处省去对(LCA)的描述),你的任务是对一棵给定的树(T)以及上面的两个节点(u,v)求出他们的(LCA)。
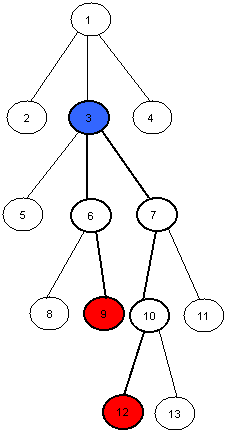
例如图中9和12号节点的LCA为3号节点
Input:
输入的第一行为数据组数(T),对于每组数据,第一行为一个整数(N(1leq Nleq1000)),节点编号从(1)到(N),接下来的(N)行里每一行开头有一个数字(M(0leq Mleq999)),(M)为第(i)个节点的子节点数量,接下来有(M)个数表示第(i)个节点的子节点编号。下面一行会有一个整数(Q(1leq Qleq1000)),接下来的(Q)行每行有两个数(u,v),输出节点(u,v)在给定树中的(LCA)。
输入数据保证只有一个根节点并且没有环。
Output:
对于每一组数据输出(Q+1)行,第一行格式为("Case i:")(没有双引号),(i)表示当前数据是第几组,接下来的(Q)行每一行一个整数表示一对节点(u,v)的(LCA)。
Sample Input:
1
7
3 2 3 4
0
3 5 6 7
0
0
0
0
2
5 7
2 7
Sample Output:
Case 1:
3
1
(Translated by @_yxl_g)l_
思路:一道求(LCA)的板子题,根据题目给出的每个点的孩子建边然后找出根结点,直接(dfs)求出深度后跑(LCA)就可以了。
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 1007
using namespace std;
int t,q,rt,tim,f[maxn][22],n,m,head[maxn],d[maxn],num;
bool vis[maxn];
struct node {
int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
e[++num].v=v;
e[num].nxt=head[u];
head[u]=num;
}
void dfs(int u, int fa) {
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v!=fa) {
f[v][0]=u;
d[v]=d[u]+1;
dfs(v,u);
}
}
}
inline int lca(int a, int b) {
if(d[a]>d[b]) swap(a,b);
for(int i=20;i>=0;--i)
if(d[a]<=d[b]-(1<<i)) b=f[b][i];
if(a==b) return a;
for(int i=20;i>=0;--i)
if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
return f[a][0];
}
int main() {
scanf("%d",&t);
while(t--) {
++tim;
memset(f,0,sizeof(f));
memset(d,0,sizeof(d));
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
num=0;
scanf("%d",&n);
for(int i=1,m;i<=n;++i) {
scanf("%d",&m);
for(int j=1,v;j<=m;++j) {
scanf("%d",&v);
ct(i,v);ct(v,i);
vis[v]=1;
}
}
for(int i=1;i<=n;++i) if(!vis[i]) rt=i;
dfs(rt,0);
for(int j=1;j<=20;++j)
for(int i=1;i<=n;++i)
f[i][j]=f[f[i][j-1]][j-1];
scanf("%d",&q);
printf("Case %d:
",tim);
for(int i=1,u,v;i<=q;++i) {
scanf("%d%d",&u,&v);
printf("%d
",lca(u,v));
}
}
return 0;
}