网络流（最大流-Dinic算法）

　摘自https://www.cnblogs.com/SYCstudio/p/7260613.html

网络流定义　

　　在图论中，网络流（Network flow）是指在一个每条边都有容量（Capacity）的有向图分配流，使一条边的流量不会超过它的容量。通常在运筹学中，有向图称为网络。顶点称为节点（Node）而边称为弧（Arc）。一道流必须匹配一个结点的进出的流量相同的限制，除非这是一个源点（Source）──有较多向外的流，或是一个汇点（Sink）──有较多向内的流。一个网络可以用来模拟道路系统的交通量、管中的液体、电路中的电流或类似一些东西在一个结点的网络中游动的任何事物。————维基百科

　最大流

　　正如可以通过将道路交通图模型化为有向图来找到从一个城市到另一个城市之间的最短路径，我们也可以将一个有向图看做是一个“流网络”并使用它来回答关于物料流动方面的问题。设想一种物料从产生它的源结点经过一个系统，流向消耗该物料的汇点这样一个过程。源结点以某种稳定的速率生成物料，汇点则以同样的速率消耗物料。从直观上看，物料在系统中任何一个点上的“流量”就是物料移动的速率。这种流网络可以用来建模很多实际问题，包括液体在管道中的流动、装配线上部件的流动、电网中电流的流动和通信网络中信息的流动。我们可以把流网络中每条有向边看做是物料的一个流通通道。每条通道有限定的容量，是物料流经该通道时的最大速率，如一条管道每小时可以流过200加仑的液体。流网络中的结点则是通道的连接点。除了源结点和终结点外，物料在其他结点上只是流过，并不积累或聚集。换句话说，物料进入一个结点速率必须与其离开该结点的速率相等。这个性质称为“流量守恒”，这里的流量守恒与Kirchhoff电流定律等价。在最大流问题中，我们希望在不违反任何容量限制的情况下，计算出从源结点运送物料到汇点的最大速率。这是与流网络有关的所有问题中最简单的问题之一(????).，这个问题可以由高效的算法解决。而且，最大流算法中的一些基本技巧可以用来解决其他网络流问题。————《算法导论》

Dinic算法

　　定义：

　　源点：只有流出去的点
　　汇点：只有流进来的点
　　流量：一条边上流过的流量
　　容量：一条边上可供流过的最大流量
　　残量：一条边上的容量-流量

几个基本性质

基本性质一：

对于任何一条流，总有流量<=容量

这是很显然的

基本性质二

对于任何一个不是源点或汇点的点u，总有

∑p∈Ek[p][u]==∑q∈Ek[u][q]（其中k[i][j]表示i到j的流量）∑p∈Ek[p][u]==∑q∈Ek[u][q]（其中k[i][j]表示i到j的流量）

这个也很显然，即一个点（除源点和汇点）的入流和出流相等

基本性质三

对于任何一条有向边(u,v)，总有

k[u][v]==−k[v][u]k[u][v]==−k[v][u]

这个看起来并不是很好理解，它的意思就是一条边的反边上的流是这条边的流的相反数，可以这么想，就是如果有k[u][v]的流从u流向v，也就相当于有-k[v][u]的流从v流向u。这条性质非常重要。

网络流最大流的求解（Ford-Fulkerson算法）

网络流的所有算法都是基于一种增广路的思想，其基本步骤如下：

1.找到一条从源点到汇点的路径，使得路径上任意一条边的残量>0（注意是大于而不是大于等于，这意味着这条边还可以分配流量），这条路径便称为增广路
2.找到这条路径上最小的F[u][v]（我们设F[u][v]表示u->v这条边上的残量即剩余流量），下面记为flow
3.将这条路径上的每一条有向边u->v的残量减去flow，同时对于起反向边v->u的残量加上flow
4.重复上述过程，直到找不出增广路，此时我们就找到了最大流

这个算法是基于增广路定理(Augmenting Path Theorem): 网络达到最大流当且仅当残留网络中没有增广路

在寻找增广路的过程中，如果我们没有建反边，那么有时候会发现找出来的路径与实际上的最大流不同，我们建这个反边是为了将原先得到的流推回去，从而得到新的流，就是给了我们反悔的机会。

这种朴素的FF算法在某种情况下可能非常低效，比如这个栗子

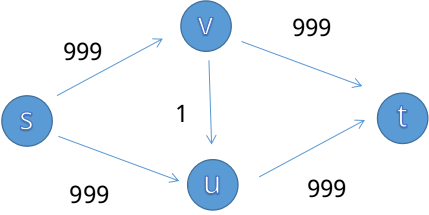
我们一眼可以看出最大流是999(s->v->t)+999(s->u->t)，但如果程序采取了不恰当的增广策略：s->v->u->t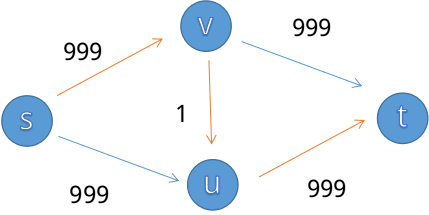

我们发现中间会加一条u->v的边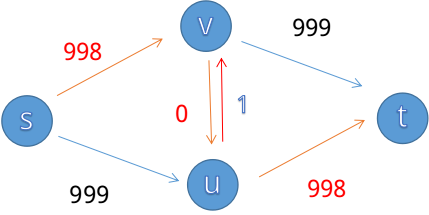

而下一次增广时：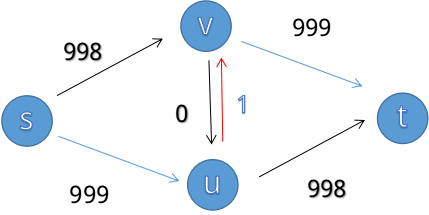

若选择了s->u->v->t

然后就变成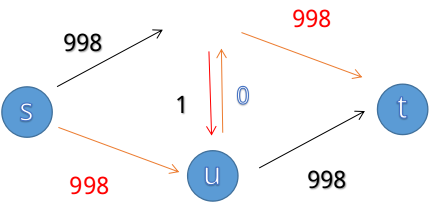

如果边上的容量更大，这个算法可能会更加低效，这时引入Dinic算法

Dinic算法

为Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点，我们根据从源点开始的bfs序列，为每一个点分配一个深度，然后我们进行若干遍dfs寻找增广路，每一次由u推出v必须保证v的深度必须是u的深度+1。

Dinic算法总结

1、首先进行bfs分层网络

2、进行dfs多路增广，并且记录残量网络和流

量。

3、重复上述过程直到不存在从s到t的路径为

止。将所有dfs的结果累加起来就是答案。将

每一次的增广路效果叠加起来就是图上每条

边的流量。

例题：HDU-3549 Flow Problem http://acm.hdu.edu.cn/showproblem.php?pid=3549

#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define INF 0x3f3f3f3f
const ll MAXN = 200 + 7;
const ll MAXM = 1e3 + 7;
const ll MOD = 1e9 + 7;
const double pi = acos(-1);
int cnt = -1, head[MAXM], dis[MAXN], cur[MAXM];
int n, m;
struct edge
{
    int to, value, net;
} e[MAXM << 1]; ///共有n*2条边
void add(int from, int to, int value)
{ ///链式前向星
    cnt++;
    e[cnt].to = to;
    e[cnt].value = value;
    e[cnt].net = head[from];
    head[from] = cnt;
}
int bfs(int st, int ed)
{ ///建立层次图
    queue<int> que;
    memset(dis, -1, sizeof(dis));
    dis[st] = 0;
    que.push(st);
    while (!que.empty())
    {
        int x = que.front();
        que.pop();
        for (int i = head[x]; i > -1; i = e[i].net)
        {
            int now = e[i].to;
            if (dis[now] == -1 && e[i].value)
            {
                que.push(now);
                dis[now] = dis[x] + 1;
            }
        }
    }
    return dis[ed] != -1;
}
int dfs(int x, int t, int maxflow)
{
    if (x == t)
        return maxflow;
    int ans = 0;
    for (int i = cur[x]; i > -1; i = e[i].net)
    { ///当前弧优化
        int now = e[i].to;
        if (dis[now] != dis[x] + 1 || e[i].value == 0 || ans >= maxflow)
            continue;
        cur[x] = i;
        int f = dfs(now, t, min(e[i].value, maxflow - ans));
        e[i].value -= f;
        e[i ^ 1].value += f; ///反向边加流量
        ans += f;
    }
    if (!ans)
        dis[x] = -1; ///炸点优化
    return ans;
}
int Dinic(int st, int ed)
{
    int ans = 0;
    while (bfs(st, ed))
    {
        memcpy(cur, head, sizeof(head));
        int k;
        while ((k = dfs(st, ed, INF)))
            ans += k;
    }
    return ans;
}
void init()
{
    cnt=-1;
    memset(head,-1,sizeof(head));
}
int main()
{
    int t;
    scanf("%d", &t);
    for (int i = 1; i <= t; i++)
    {
        init();
        scanf("%d%d", &n, &m);
        while (m--)
        {
            int u, v, t;
            scanf("%d%d%d", &u, &v, &t);
            add(u, v, t);
            add(v, u, 0);
        }
        printf("Case %d: %d
", i, Dinic(1, n));
    }
    return 0;
}