You have a convex n-sided polygon where each vertex has an integer value. You are given an integer array values where values[i] is the value of the ith vertex (i.e., clockwise order).
You will triangulate the polygon into n - 2 triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all n - 2 triangles in the triangulation.
Return the smallest possible total score that you can achieve with some triangulation of the polygon.
Example 1:
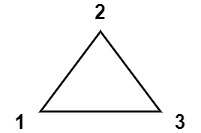
Input: values = [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.
Example 2:
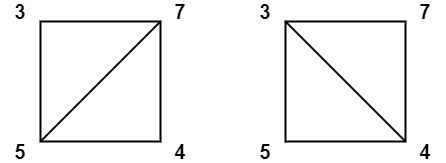
Input: values = [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.
The minimum score is 144.
Example 3:
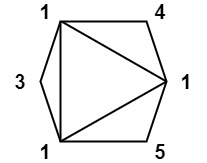
Input: values = [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.
Constraints:
n == values.length3 <= n <= 501 <= values[i] <= 100
这道题说有一个N边形,让我们连接不相邻的顶点,从而划分出三角形,最多可以划分出 N-2 个三角形,每划分出一个三角形,得分是三个顶点的乘积,问最小的得分是多少。题目并不是很难理解,而且还配了图,多边形的三角形化是计算机图形学中的一个重要知识点,当然这道题并不需要过多的几何知识,只是存粹的求极值的问题。对于这类求极值的问题,一般会考虑贪婪算法和动态规划,这里贪婪算法显然不适用,因为顶点值的大小是无规律的,贪婪算法到达的局部最优解并不能保证是全局最优。而动态规划的本质上其实还是计算出了所有的情况,跟暴力搜索的法的区别在于保存了中间结果到 dp 数组,从而避免了大量的重复的计算,大大提高了时间复杂度。首先要来定义 DP 数组,这里一维数组肯定是不够用的,因为需要保存区间信息,所以这里用个二维数组,其中 dp[i][j] 表示从顶点i到顶点j为三角形的一条边,可以组成的所有的三角形的最小得分。接下来推导状态转移方程,由于三角形的一条边已经确定了,接下来就要找另一个顶点的位置,这里需要遍历所有的情况,使用一个变量k,遍历区间 (i, j) 中的所有的顶点,由顶点i,j,和k组成的三角形的得分是 A[i] * A[k] * A[j] 可以直接算出来,这个三角形将整个区间分割成了两部分,分别是 (i, k) 和 (k, j),这两个区间的最小得分值可以直接从 dp 数组中取得,分别是 dp[i][k] 和 dp[k][j],这样状态转移方程就有了,用 dp[i][k] + A[i] * A[k] * A[j] + dp[k][j] 来更新 dp[i][j],为了防止整型越界,不能直接将 dp 数组都初始化为整型最大值 INT_MAX,而是在更新的时候,判断若 dp[i][j] 为0时,用 INT_MAX,否则用其本身值,最终的结果保存在 dp[0][n-1] 中,参见代码如下:
解法一:
class Solution {
public:
int minScoreTriangulation(vector<int>& A) {
int n = A.size();
vector<vector<int>> dp(n, vector<int>(n));
for (int i = n - 1; i >= 0; --i) {
for (int j = i + 1; j < n; ++j) {
for (int k = i + 1; k < j; ++k) {
dp[i][j] = min(dp[i][j] == 0 ? INT_MAX : dp[i][j], dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]);
}
}
}
return dp[0][n - 1];
}
};
再来看一种同样的 DP 解法,和上面的区别是 dp 数组更新的顺序不同,之前说过了更新大区间的 dp 值需要用到小区间的 dp 值,这里是按照区间的大小来更新的,从2更新到n,然后确定区间 (i, j) 的大小为 len,再遍历中间所有的k,状态转移方程还是跟上面一样的。这种更新方法在其他的题目也有用到,最典型的就是那道 Burst Balloons,参见代码如下:
解法二:
class Solution {
public:
int minScoreTriangulation(vector<int>& A) {
int n = A.size();
vector<vector<int>> dp(n, vector<int>(n));
for (int len = 2; len < n; ++len) {
for (int i = 0; i + len < n; ++i) {
int j = i + len;
dp[i][j] = INT_MAX;
for (int k = i + 1; k < j; ++k) {
dp[i][j] = min(dp[i][j], dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]);
}
}
}
return dp[0][n - 1];
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1039
类似题目:
参考资料:
https://leetcode.com/problems/minimum-score-triangulation-of-polygon/