You are given a grid of size N x N, and each cell of this grid has a lamp that is initially turned off.
You are also given an array of lamp positions lamps, where lamps[i] = [rowi, coli] indicates that the lamp at grid[rowi][coli] is turned on. When a lamp is turned on, it illuminates its cell and all other cells in the same row, column, or diagonal.
Finally, you are given a query array queries, where queries[i] = [rowi, coli]. For the ith query, determine whether grid[rowi][coli] is illuminated or not. After answering the ith query, turn off the lamp at grid[rowi][coli] and its 8 adjacent lamps if they exist. A lamp is adjacent if its cell shares either a side or corner with grid[rowi][coli].
Return an array of integers ans,* where ans[i] should be 1 if the lamp in the ith query was illuminated, or 0 if the lamp was not.*
Example 1:
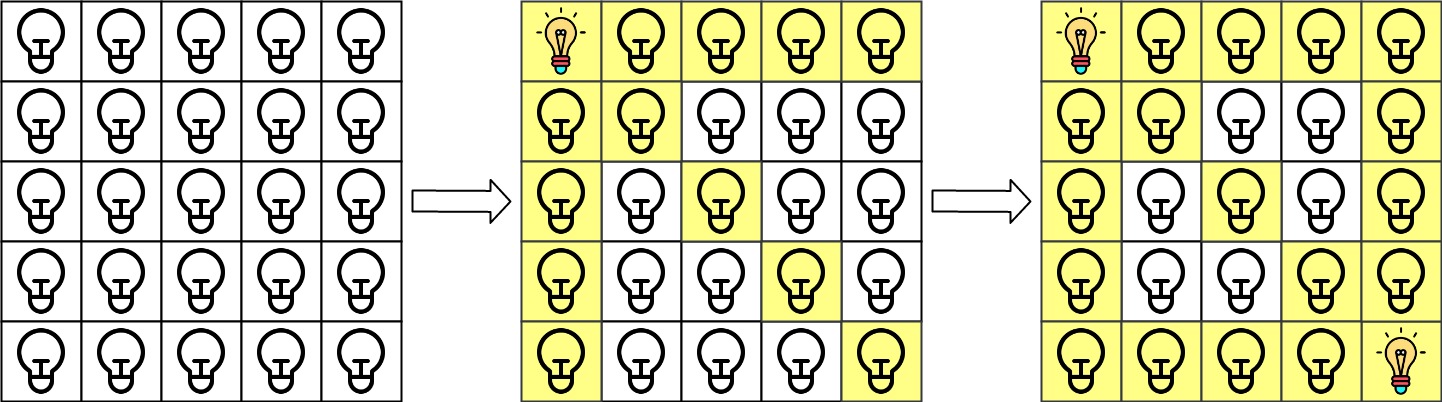
Input: N = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
Output: [1,0]
Explanation: We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid[0][0] then turning on the lamp at grid[4][4].
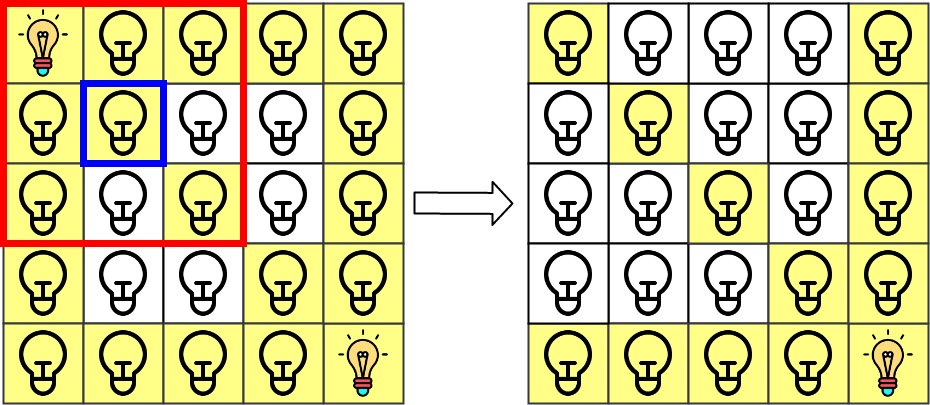
The 0th query asks if the lamp at grid[1][1] is illuminated or not (the blue square). It is illuminated, so set ans[0] = 1. Then, we turn off all lamps in the red square.
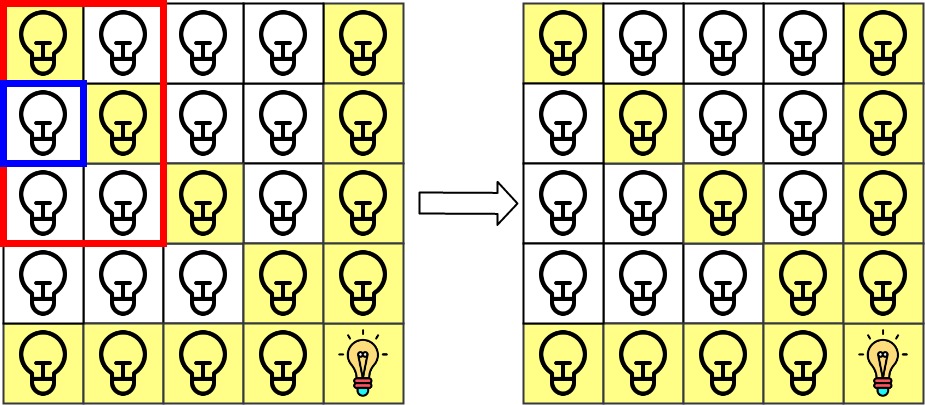
The 1st query asks if the lamp at grid[1][0] is illuminated or not (the blue square). It is not illuminated, so set ans[1] = 0. Then, we turn off all lamps in the red rectangle.
Example 2:
Input: N = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
Output: [1,1]
Example 3:
Input: N = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
Output: [1,1,0]
Constraints:
1 <= N <= 1090 <= lamps.length <= 20000lamps[i].length == 20 <= lamps[i][j] < N0 <= queries.length <= 20000queries[i].length == 20 <= queries[i][j] < N
这道题给了一个 NxN 的格子,说是每个位置都有一个台灯,初始时都是熄灭的,现在给了一个二维数组 lamps,是一些开着的台灯的位置,说是每个开着的台灯都可以照亮该台灯所在的行,列,对角线,和逆对角线上所有的位置。现在又给了一个 queries 数组,是一系列的位置,问该位置是否被照亮,并且说得到结果之后,要关上该位置即周围八个相邻位置上所有开着的台灯。这里的台灯实际上跟国际象棋中的皇后是一样的,之前也做过N皇后问题 N-Queens,所以我们知道如何判断任意两个位置放皇后是否冲突,正好也就是这里的判断某位置是否会被照亮。博主最开始想到的方法是,先把所有亮着的台灯放到一个 TreeSet 中,然后遍历所有 query,对于每个位置,遍历所有的亮着的台灯,调用N皇后中的判断冲突的方法,就可以知道该位置是否被照亮,然后再将其和周围8个相邻位置的亮着的台灯关上,但是很不幸,这种方法超时 TLE 了,所以需要进一步的优化。上面的方法主要耗时的地方在于遍历每个台灯,并且判断能否照到 query 位置,当亮着的台灯非常的多的时候,就会非常耗时间。想办法用些更巧妙的方法,这里可以统计每行,每列,每条对角线,以及逆对角线上亮着的灯的个数,用 HashMap 分别建立映射,只要映射值大于0,则对应位置上一定会被照亮。台灯的横纵坐标分别映射行和列,横纵坐标之差映射对角线,横纵坐标之和映射逆对角线,然后还有一个 TreeSet 用来保存亮着的台灯的坐标。然后遍历所有 query,利用该 query 的横纵坐标去上述4个 HashMap 中找,只要任意一个映射值大于0,则该位置就是被照亮的。然后遍历该位置以及周围八个相邻的位置,若有亮着的台灯,将所有 HashMap 的映射值自减1,并且移出 TreeSet 即可,参见代码如下:
class Solution {
public:
vector<int> gridIllumination(int N, vector<vector<int>>& lamps, vector<vector<int>>& queries) {
vector<int> res(queries.size());
vector<vector<int>> dirs{{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}, {0, 0}};
unordered_map<int, int> rowMap, colMap, diagMap, invDiagMap;
set<vector<int>> lampSet;
for (auto &lamp : lamps) {
++rowMap[lamp[0]];
++colMap[lamp[1]];
++diagMap[lamp[0] - lamp[1]];
++invDiagMap[lamp[0] + lamp[1]];
lampSet.insert({lamp[0], lamp[1]});
}
for (int i = 0; i < queries.size(); ++i) {
int x0 = queries[i][0], y0 = queries[i][1];
if (rowMap[x0] > 0 || colMap[y0] > 0 || diagMap[x0 - y0] > 0 || invDiagMap[x0 + y0] > 0) {
res[i] = 1;
}
for (auto &dir : dirs) {
int x = x0 + dir[0], y = y0 + dir[1];
if (lampSet.count({x, y})) {
--rowMap[x];
--colMap[y];
--diagMap[x - y];
--invDiagMap[x + y];
lampSet.erase({x, y});
}
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/1001
类似题目:
参考资料:
https://leetcode.com/problems/grid-illumination/