For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes root1 and root2.
Example 1:
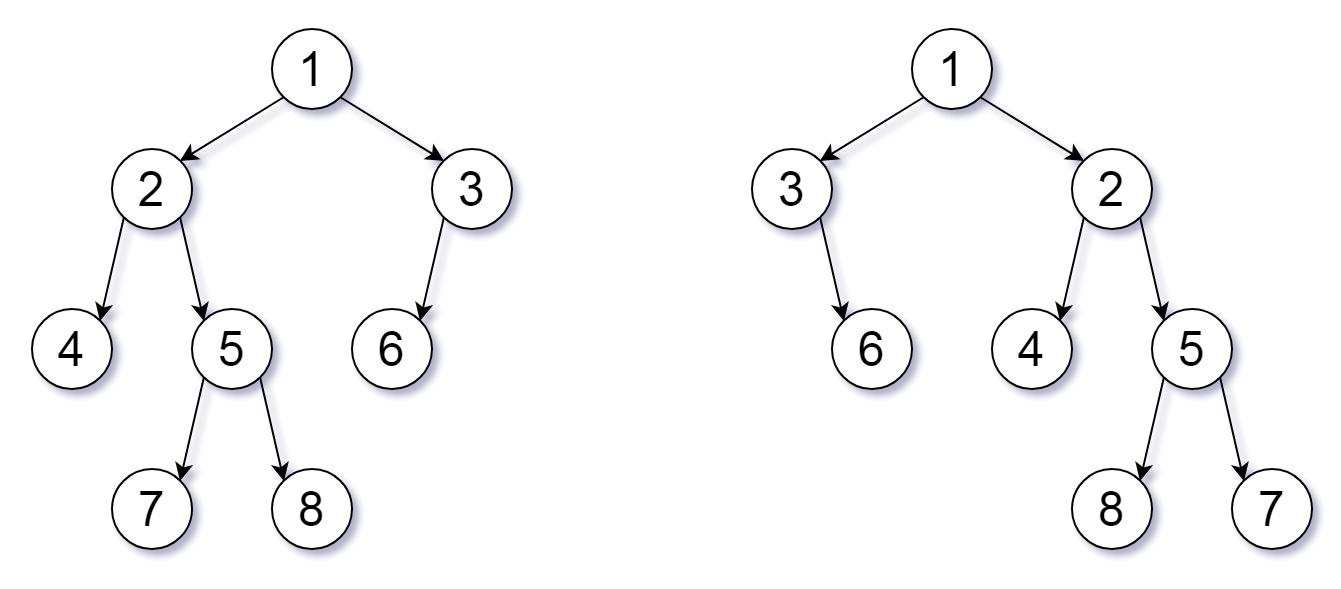
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.
Note:
- Each tree will have at most
100nodes. - Each value in each tree will be a unique integer in the range
[0, 99].
这道题说是可以交换二叉树中任意一个的结点的左右子结点,其实也就是交换了左右子树。现在给了两棵二叉树,问能不能通过交换子结点操作来变成相同的树。博主拿到题目以后,扫了一眼难度,是 Medium,大概猜到了这道题目不会过于复杂。对于二叉树的题目,根据博主多年的刷题经验,十有八九都是用递归,这道题也不例外。首先来分析一些 corner case,当两个给定的根结点都为空的时候,此时应该返回 true 的,因为两个空树可以看作是相等的。其次当一个为空,另一个不为空的时候,一定是返回 false 的,或者当两个根结点的值不相等时,也是返回 false 的。当两个根结点值相同时,接下来就是要对子结点调用递归了,若是对两个左右子结点分别调用递归函数均返回 true,说明整个肯定是返回 true 的没有问题,即便返回 false 了也不要紧,因为这里还可以利用交换子结点的性质再调用一遍递归函数,此时 root1 的左子结点对应 root2 的右子结点,root1 的右子结点对应 root2 的左子结点,这个若返回 true 的话也行,参见代码如下:
class Solution {
public:
bool flipEquiv(TreeNode* root1, TreeNode* root2) {
if (!root1 && !root2) return true;
if (!root1 || !root2 || root1->val != root2->val) return false;
return (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right)) || (flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left));
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/951
参考资料:
https://leetcode.com/problems/flip-equivalent-binary-trees/