博客作业03--栈和队列

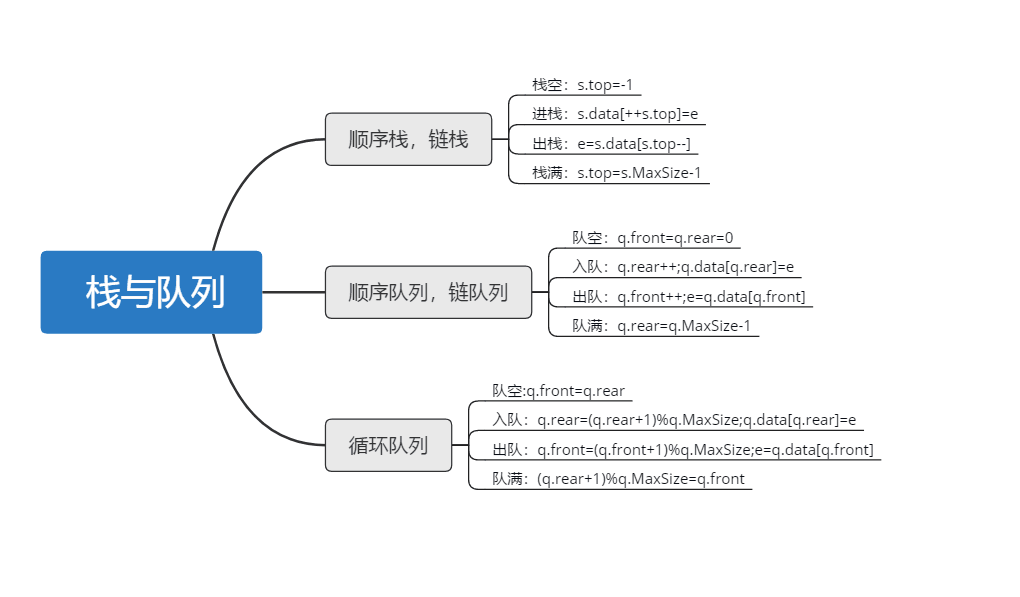
1.学习总结

2.PTA实验作业

题目1：7-1 jmu-字符串是否对称

设计思路：

定义一个栈和一个数组，
  将数据储存在栈里，同时储存在数组里
  i=0;
  while(s.top!=-1){
  	判断pop(s,e)  e==str[i];
  	i++;
	  if(不同) break;
  } 
  if(i<s.top)  输出no
  else 输出yes 

代码截图:

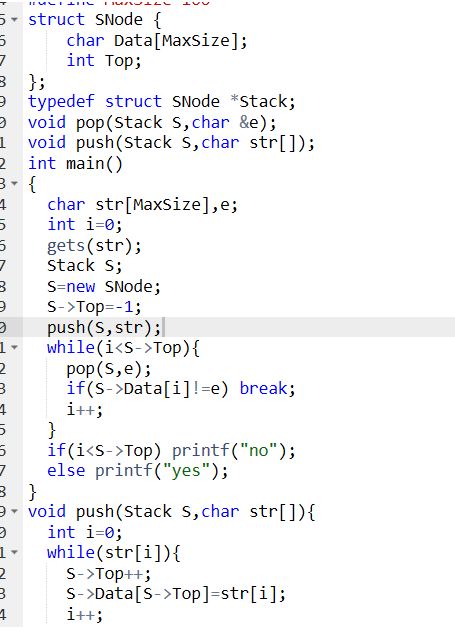
PTA提交列表说明:

我的代码一直只对一半，然后后面我改了之后，明明和答案全对但是他就是一直出现段错误，后面去借鉴同学的代码
还是觉得不知道自己错在哪里。

题目2：7-1 jmu-报数游戏

设计思路：

定义一个队列
 输入max,num
 if(num>max) 输出error
 for(i=1 to max) 将i入队 
 定义一个值sum=num
 while(Q){
 	while(sum--) 将第一个数出队在入队
	出队，且输出
	sum=num; 
 } 
 end

代码截图:

PTA提交列表说明:

一开始定义错误了结构体，后面把结构体改了过来，就行了。

题目2：7-2 银行业务队列简单模拟

设计思路：

 定义两个队列和一个数组
 先将数据放入数组中
 while(a[i++]){
 if(为奇数）存储队列number1中
 else   存入number2中
}
 while（number1&&number2）{
  number1出队
  number1出队
  number2出队
}
 if(number1) 将number2其余的数出队
 if(number2) 将number1其余的数出队

代码截图:

PTA提交列表说明:

本题一开始我想到了用数组的方法来做，我先用数组的方法来做了做对了在用队列的方法来做了，所以本题没出现较大的问题。

3.截图本周题目集的PTA最后排名

3.1 栈PTA排名

3.2 队列PTA排名

3.3 我的总分：205

4. 阅读代码

列车调度

#include <bits/stdc++.h>  
  
using namespace std;  
const int MAXN=40;  
int n,m;  
set<int>q;  
int main()  
{  
    scanf("%d",&n);  
    int x;  
    for(int i=0;i<n;++i)  
    {  
        scanf("%d",&x);  
        if(q.upper_bound(x)!=q.end())  
        {  
            q.erase(q.upper_bound(x));  
        }  
        q.insert(x);  
    }  
    printf("%u
",q.size());  
    return 0;  
}  

https://blog.csdn.net/qq_33362864/article/details/61422781
iteratorlower_bound( const key_type &key ): 返回一个迭代器，指向键值>= key的第一个元素。
iterator upper_bound( const key_type &key ):返回一个迭代器，指向键值>key的第一个元素。
end函数：返回一个当前vector容器中末尾元素的迭代器
q.insert(x)：将数据 x 插入增序表

5. 代码Git提交记录截图