我们前文说过,有关最短路径除了Floyed算法之外,还有许多更加好的方法。这里讲一下有关 Bellman-Ford和SPFA的知识
Bellman-Ford:复杂度O(VE)
有关Bellman-Ford,也不是特别的重要,可以说算是对于SPFA的一个铺垫(有更好的方法还用什么laji更慢的算法呢?)【这里有一个迭代搞的我很懵,这里暂且看做是有关松弛的操作】
Bellman-Ford算法是求含负权图的单源最短路径的一种算法,效率较低,代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在n-1次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成。
从这里大家可以看出Bellman-Ford和SPFA在一定程度上的弊端:图中有负环则无法出答案。但可以对其进行一步判断
我们应当明确一点:Bellman-Ford算法是用来解决单源最短路问题的。(恩,没毛病)
这里需要进行多次的松弛操作,每一次成功的松弛操作,都意味着我们发现了一条新的最短路。所以这个方法显然是对的,但是显然laji够慢
(下面这一段是黈的,毕竟本蒟蒻不会迭代QAQ)
注意:1.只有上一次迭代中松弛过的点才有可能参与下一次迭代的松弛操作。
2.迭代的实际意义:每次迭代k中,我们找到了经历了k条边的最短路。
3.没有点能够被“松弛”时,迭代结束
//由于我不太写Bellman-Ford的代码,这里用的是百度百科的,害怕误人子弟qwq
#include<iostream> #include<cstdio> using namespace std; #define MAX 0x3f3f3f3f #define N 1010 int nodenum, edgenum, original; //点,边,起点 typedef struct Edge //边 { int u, v; int cost; }Edge; Edge edge[N]; int dis[N], pre[N]; bool Bellman_Ford() { for(int i = 1; i <= nodenum; ++i) //初始化 dis[i] = (i == original ? 0 : MAX); for(int i = 1; i <= nodenum - 1; ++i) for(int j = 1; j <= edgenum; ++j) if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛(顺序一定不能反~) { dis[edge[j].v] = dis[edge[j].u] + edge[j].cost; pre[edge[j].v] = edge[j].u; } bool flag = 1; //判断是否含有负权回路 for(int i = 1; i <= edgenum; ++i) if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost) { flag = 0; break; } return flag; } void print_path(int root) //打印最短路的路径(反向) { while(root != pre[root]) //前驱 { printf("%d-->", root); root = pre[root]; } if(root == pre[root]) printf("%d ", root); } int main() { scanf("%d%d%d", &nodenum, &edgenum, &original); pre[original] = original; for(int i = 1; i <= edgenum; ++i) { scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost); } if(Bellman_Ford()) for(int i = 1; i <= nodenum; ++i) //每个点最短路 { printf("%d ", dis[i]); printf("Path:"); print_path(i); } else printf("have negative circle "); return 0; }
SPFA:复杂度O(MN)【这里的M在一般不毒瘤的题里是2,N就是边数】
SPFA 算法是 Bellman-Ford算法的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同,为 O(VE)。
相对于Dijkstra算法来说有相似之处,但又不同(貌似Dijkstra更稳一些qwq)
算法大致流程是用一个队列来进行维护。 初始时将源加入队列。 每次从队列中取出一个元素,并对所有与他相邻的点进行松弛,若某个相邻的点松弛成功,则将其入队。 直到队列为空时算法结束。
这样就可以大幅度的减少复杂度(毒瘤题除外)
因为本蒟蒻初学,这里发一个简单的代码
可以过洛谷P3371 【模板】单源最短路径(弱化版)
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入输出格式
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15;
对于40%的数据:N<=100,M<=10000;
对于70%的数据:N<=1000,M<=100000;
对于100%的数据:N<=10000,M<=500000。保证数据随机。
对于真正 100% 的数据,请移步P4779。请注意,该题与本题数据范围略有不同。
样例说明:
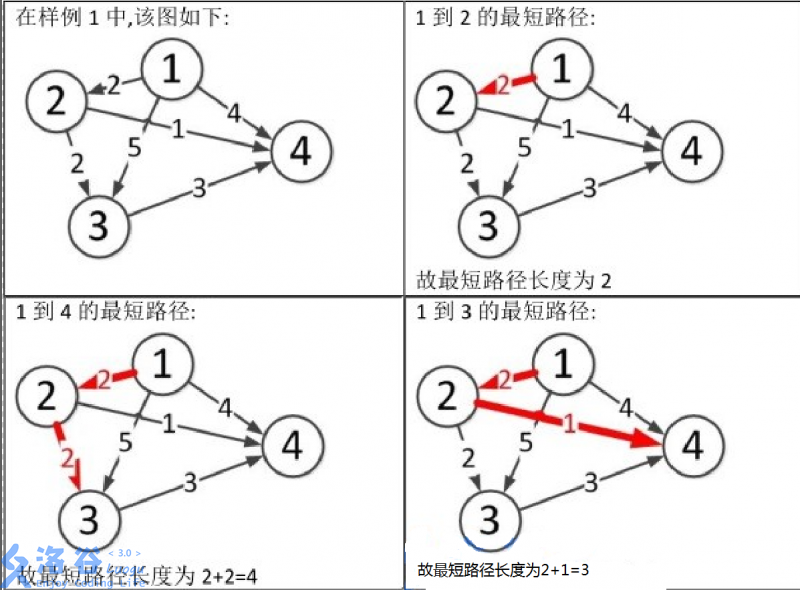
图片1到3和1到4的文字位置调换
#include<cstdio> #include<iostream> #include<algorithm> #include<queue> using namespace std; const int inf=2147483647; int n,m,s; int dis[10008],vis[10008],head[10008],num_edge; struct Edge{ int next,to,dis; }edge[500008]; queue <int> q; void addedge(int from,int to,int dis) { num_edge++; edge[num_edge].next=head[from]; edge[num_edge].to=to; edge[num_edge].dis=dis; head[from]=num_edge; } void spfa() { for(int i=1;i<=n;++i) { dis[i]=inf; vis[i]=0; } dis[s]=0; vis[s]=1; q.push(s); while(!q.empty()) { int u=q.front(); q.pop(); vis[u]=0; for(int i=head[u];i;i=edge[i].next) { int v=edge[i].to; if(dis[v]>dis[u]+edge[i].dis) { dis[v]=dis[u]+edge[i].dis; if(!vis[v]) { q.push(v); vis[v]=1; } } } } } int main() { scanf("%d %d %d",&n,&m,&s); for(int i=1;i<=m;++i) { int u,v,d; scanf("%d %d %d",&u,&v,&d); addedge(u,v,d); } spfa(); for(int i=1;i<=n;++i) { if(i==s) printf("0 "); else printf("%d ",dis[i]); } return 0; }