在程序开发中,我们常遇到用树型结构来表示某些数据间的关系,如企业的组织架构、商品的分类、操作栏目等,目前的关系型数据库都是以二维表的形式记录存储数据,而树型结构的数据如需存入二维表就必须进行Schema设计。最近对此方面比较感兴趣,专门做下梳理,如下为常见的树型结构的数据:

一、邻接表
其中最简单的方法是:Adjacency List(邻接列表模式)。简单的说是根据节点之间的继承关系,显现的描述某一节点的父节点,从而建立二位的关系表。表结构通常设计为{Node_id,Parent_id},如下图:
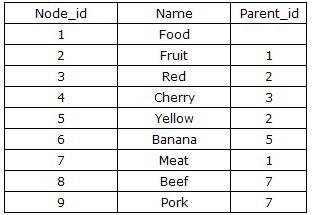
这种方案的优点很明显:结构简单易懂,由于互相之间的关系只由一个parent_id维护,所以增删改都是非常容易,只需要改动和他直接相关的记录就可以。
缺点当然也是非常的突出:由于直接地记录了节点之间的继承关系,因此对Tree的任何CRUD操作都将是低效的,这主要归根于频繁的“递归”操作,递归过程不断地访问数据库,每次数据库IO都会有时间开销。举个例子,如果想要返回所有水果,也就是水果的所有子孙节点,看似很简单的操作,就需要用到一堆递归。
当然,这种方案并非没有用武之地,在树的层级比较少的时候就非常实用。这种方法的优点是存储的信息少,查直接上司和直接下属的时候很方便,缺点是多级查询的时候很费劲。所以当只需要用到直接上下级关系的时候,用这种方法还是不错的,可以节省很多空间。
二、物化路径
物化路径其实更加容易理解,其实就是在创建节点时,将节点的完整路径进行记录。以下图为例:
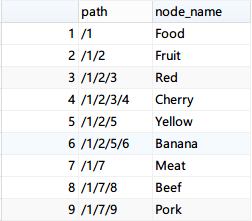
此种方案借助了unix文件目录的思想,主要时以空间换时间。
// 查询某一节点下的所有子节点:(以Fruit为例)
SET @path = (SELECT path FROM pathTree WHERE node_name = 'Fruit');
SELECT * FROM pathTree WHERE path like CONCAT(@path,'/%');
// 如何查询直属子节点?需要采用MySQL的正则表达式查询:
SET @path = (SELECT path FROM pathTree WHERE node_name = 'Fruit');
SELECT * FROM pathTree WHERE path REGEXP CONCAT(@path,'/','[0-9]$');
// 查询任意节点的所有上级:(以Yellow为例):
SET @path = (SELECT path FROM pathTree WHERE node_name = 'Yellow');
SELECT * FROM pathTree WHERE @path LIKE CONCAT(path, '%') AND path <> @path;
// 插入新增数据:
SET @parent_path = ( SELECT path FROM pathTree WHERE node_name = 'Fruit');
INSERT INTO pathtree (path,node_name) VALUES (CONCAT(@parent_path,'/',LAST_INSERT_ID()+1),'White')
此方案的缺点是树的层级太深有可能会超过PATH字段的长度,所以其能支持的最大深度并非无限的。
如果层级数量是确定的,可以再将所有的列都展开,如下图,比较适用于于类似行政区划、生物分类法(界、门、纲、目、科、属、种)这些层级确定的内容。
三、左右值编码
在基于数据库的一般应用中,查询的需求总要大于删除和修改。为了避免对于树形结构查询时的“递归”过程,基于Tree的前序遍历设计一种全新的无递归查询、无限分组的左右值编码方案,来保存该树的数据。
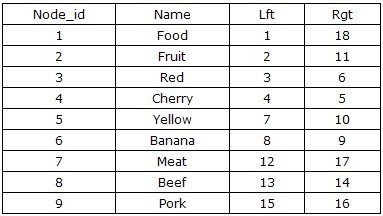
第一次看见这种表结构,相信大部分人都不清楚左值(Lft)和右值(Rgt)是如何计算出来的,而且这种表设计似乎并没有保存父子节点的继承关系。但当你用手指指着表中的数字从1数到18,你应该会发现点什么吧。对,你手指移动的顺序就是对这棵树进行前序遍历的顺序,如下图所示。当我们从根节点Food左侧开始,标记为1,并沿前序遍历的方向,依次在遍历的路径上标注数字,最后我们回到了根节点Food,并在右边写上了18。
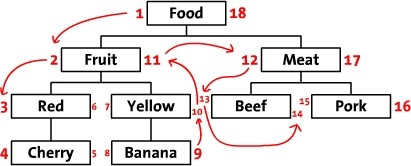
依据此设计,我们可以推断出所有左值大于2,并且右值小于11的节点都是Fruit的后续节点,整棵树的结构通过左值和右值存储了下来。然而,这还不够,我们的目的是能够对树进行CRUD操作,即需要构造出与之配套的相关算法。按照深度优先,由左到右的原则遍历整个树,从1开始给每个节点标注上left值和right值,并将这两个值存入对应的name之中。
本方案的优点是查询非常的方便,缺点就是每次插入删除数据涉及到的更新内容太多,如果树非常大,插入一条数据可能花很长的时间。所以不推荐,了解下就行,也不打算深入研究,想研究的可以查其他资料。
四、闭包表
将Closure Table翻译成闭包表不知道是否合适,闭包表的思路和物化路径差不多,都是空间换时间,Closure Table,一种更为彻底的全路径结构,分别记录路径上相关结点的全展开形式。能明晰任意两结点关系而无须多余查询,级联删除和结点移动也很方便。但是它的存储开销会大一些,除了表示结点的Meta信息,还需要一张专用的关系表。
// 主表
CREATE TABLE nodeInfo (
node_id INT NOT NULL AUTO_INCREMENT,
node_name VARCHAR (255),
PRIMARY KEY (`node_id`)
) DEFAULT CHARSET = utf8;
// 关系表
CREATE TABLE nodeRelationship (
ancestor INT NOT NULL,
descendant INT NOT NULL,
distance INT NOT NULL,
PRIMARY KEY (ancestor, descendant)
) DEFAULT CHARSET = utf8;
其中
- Ancestor代表祖先节点
- Descendant代表后代节点
- Distance 祖先距离后代的距离
添加数据(创建存储过程)
CREATE DEFINER = `root`@`localhost` PROCEDURE `AddNode`(`_parent_name` varchar(255),`_node_name` varchar(255))
BEGIN
DECLARE _ancestor INT;
DECLARE _descendant INT;
DECLARE _parent INT;
IF NOT EXISTS(SELECT node_id From nodeinfo WHERE node_name = _node_name)
THEN
INSERT INTO nodeinfo (node_name) VALUES(_node_name);
SET _descendant = (SELECT node_id FROM nodeinfo WHERE node_name = _node_name);
INSERT INTO noderelationship (ancestor,descendant,distance) VALUES(_descendant,_descendant,0);
IF EXISTS (SELECT node_id FROM nodeinfo WHERE node_name = _parent_name)
THEN
SET _parent = (SELECT node_id FROM nodeinfo WHERE node_name = _parent_name);
INSERT INTO noderelationship (ancestor,descendant,distance) SELECT ancestor,_descendant,distance+1 from noderelationship where descendant = _parent;
END IF;
END IF;
END;
完成后2张表的数据大致是这样的:(注意:每个节点都有一条到其本身的记录。)


// 查询Fruit下所有的子节点
SELECT
n3.node_name
FROM
nodeinfo n1
INNER JOIN noderelationship n2 ON n1.node_id = n2.ancestor
INNER JOIN nodeinfo n3 ON n2.descendant = n3.node_id
WHERE
n1.node_name = 'Fruit'
AND n2.distance != 0
// 查询Fruit下直属子节点:
SELECT
n3.node_name
FROM
nodeinfo n1
INNER JOIN noderelationship n2 ON n1.node_id = n2.ancestor
INNER JOIN nodeinfo n3 ON n2.descendant = n3.node_id
WHERE
n1.node_name = 'Fruit'
AND n2.distance = 1
// 查询Fruit所处的层级:
SELECT
n2.*, n3.node_name
FROM
nodeinfo n1
INNER JOIN noderelationship n2 ON n1.node_id = n2.descendant
INNER JOIN nodeinfo n3 ON n2.ancestor = n3.node_id
WHERE
n1.node_name = 'Fruit'
ORDER BY
n2.distance DESC
然后是新增节点:即为给某一个节点新增子节点,假设该节点还是B,现在给B节点新增一个子节点E
public insert(Node a,Node b){
//1.将自己记录下来
conn.excuteSql(insert into releation values(a,a,0));
//2.查找a的祖先和自己,并告知他们,他们新增的子孙b
List<Releation> ancestors = conn.excuteSql(select r.ancestor from releation r where r.descendant=a order by distacne);
for(Releation r : ancestors){
conn.excuteSql(insert into releation values(r.ancestor,b,r.distacne+1))
}
}
缺点很显而易见,他的存储和更新开销太大。
以上所述存储方案,并没有绝对的优劣之分,适用场合不同而已。可以根据情况自己选用。