
动态规划
动态规划是寻找最优解的方法,在具体的题型中又可以分为一维列表, 二维列表等。现在所总结的是二维列表的动态规划,一维列表的题目请看动态规划系列。
- 最小路径和
- 不同路径
- 不同路径II
- 编辑距离
- 完全平方数
- 最大正方形
- 回文子串
- 买卖股票1
- 买卖股票2
最小路径和
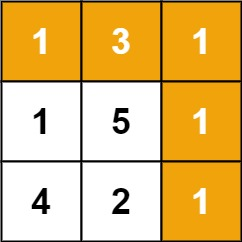
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。

def minPathSum(grid):
rows = len(grid)
cols = len(grid[0])
for x in range(rows):
for y in range(cols):
if x == 0 and y == 0:
continue
elif x == 0:
grid[x][y] = grid[x][y-1] + grid[x][y]
elif y == 0:
grid[x][y] = grid[x-1][y] + grid[x][y]
else:
grid[x][y] = min(grid[x-1][y],grid[x][y-1]) + grid[x][y]
return grid[-1][-1]
grid = [[1,3,1],[1,5,1],[4,2,1]]
res = minPathSum(grid)
print(res)
不同路径
有多少种走法
def minPathSum(grid):
rows = len(grid)
cols = len(grid[0])
for x in range(rows):
for y in range(cols):
if x == 0 and y == 0:
grid[x][y] = 0
elif x == 0:
grid[x][y] = 1
elif y == 0:
grid[x][y] = 1
else:
grid[x][y] = grid[x-1][y] + grid[x][y-1]
return grid[-1][-1]
grid = [[1,2,3],[4,5,6]]
res = minPathSum(grid)
print(res)
不同路径 II
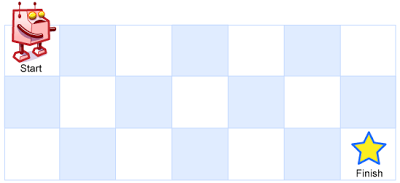
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-paths-ii

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
思路:
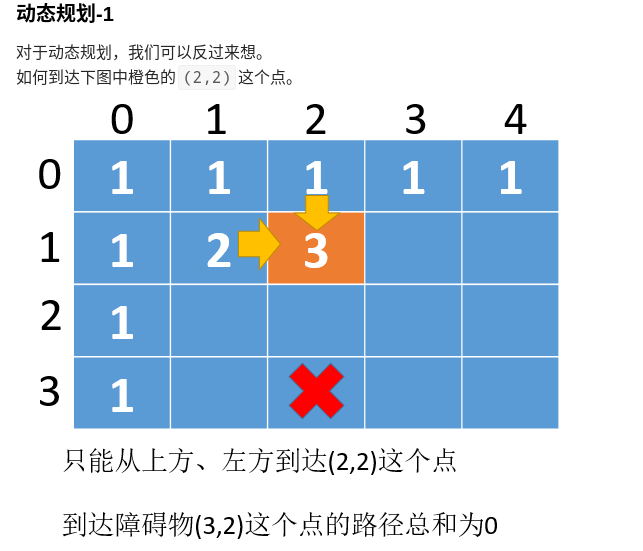

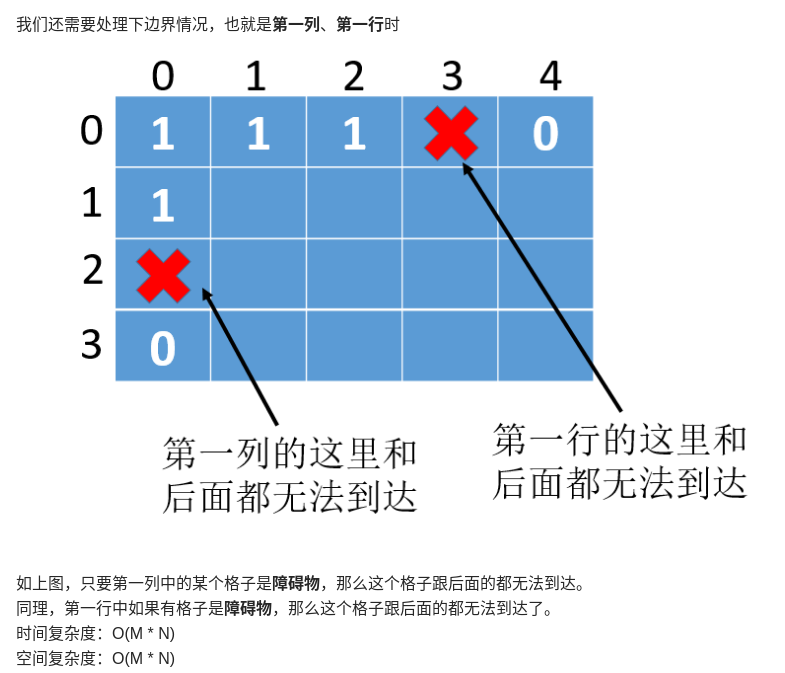
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
n = len(obstacleGrid)
m = len(obstacleGrid[0])
dp = [[0] * m for _ in range(n)]
#(0,0)这个格子可能有障碍物
dp[0][0] = 0 if obstacleGrid[0][0] else 1
#处理第一列
for i in range(1, n):
if obstacleGrid[i][0] == 1 or dp[i - 1][0] == 0:
dp[i][0] = 0
else:
dp[i][0] = 1
#处理第一行
for j in range(1, m):
if obstacleGrid[0][j] == 1 or dp[0][j - 1] == 0:
dp[0][j] = 0
else:
dp[0][j] = 1
for i in range(1, n):
for j in range(1, m):
#如果当前格子是障碍物
if obstacleGrid[i][j] == 1:
dp[i][j] = 0
#路径总数来自于上方(dp[i-1][j])和左方(dp[i][j-1])
else:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[-1][-1]
编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/edit-distance


class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n1 = len(word1)
n2 = len(word2)
dp = [[0 for _ in range(n2+1)] for _ in range(n1+1)]
for i in range(1, n2+1):
dp[0][i] = dp[0][i-1] + 1
for i in range(1, n1+1):
dp[i][0] = dp[i-1][0] + 1
for i in range(1, n1+1):
for j in range(1, n2+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
return dp[-1][-1]
完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
这道题本质上是找硬币问题。可以将题目转化一下:找到一个数的平方根,计算出平方根以内的平方数。如12,平方根向上取整是4,那么能够组成12的平方数就在4以内,即1,4,9,16之中。然后就是凑硬币,用不限个数的1,4,9,16,凑成12,硬币书最少的。
根据以上的分析写出如下代码:
class Solution:
def numSquares(self, n: int) -> int:
import math
sqrt_value = math.ceil(math.sqrt(n))
numbers = [i**2 for i in range(1, sqrt_value+1)]
dp = [0] * (n+1)
for i in range(1,n+1):
temp_list = []
for j in numbers:
if i >= j:
temp_list.append(dp[i-j]+1)
else:
break
dp[i] = min(temp_list)
return dp[-1]
最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:
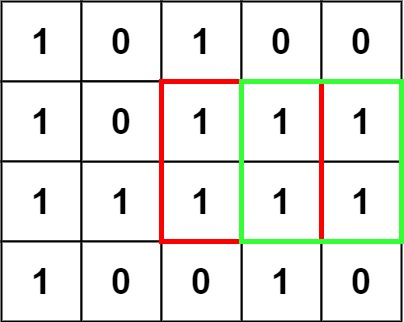
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
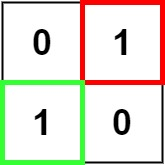
思路:
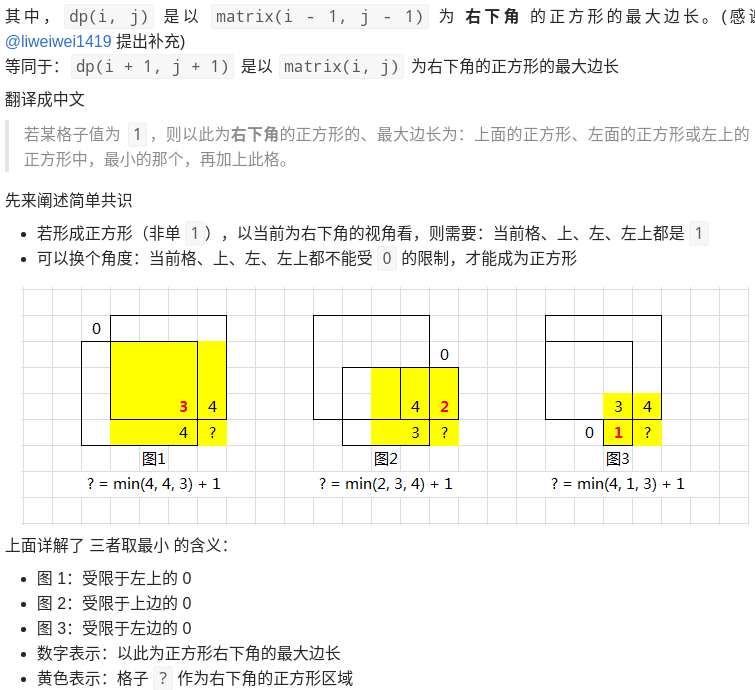

class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
row = len(matrix)
col = len(matrix[0])
dp = [ [0 for _ in range(col+1)] for _ in range(row+1)]
max_area = 0
for i in range(row):
for j in range(col):
if matrix[i][j] == '1':
dp[i+1][j+1] = min(dp[i][j], dp[i+1][j], dp[i][j+1]) + 1
max_area = max(max_area, dp[i+1][j+1])
return max_area ** 2
回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:"abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:"aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
方法:
- 动态规划法
首先这一题可以使用动态规划来进行解决:
状态:dp[i][j] 表示字符串s在[i,j]区间的子串是否是一个回文串。
状态转移方程:当 s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1]) 时,dp[i][j]=true,否则为false
这个状态转移方程是什么意思呢?
当只有一个字符时,比如 a 自然是一个回文串。
当有两个字符时,如果是相等的,比如 aa,也是一个回文串。
当有三个及以上字符时,比如 ababa 这个字符记作串 1,把两边的 a 去掉,也就是 bab 记作串 2,可以看出只要串2是一个回文串,那么左右各多了一个 a 的串 1 必定也是回文串。所以当 s[i]==s[j] 时,自然要看 dp[i+1][j-1] 是不是一个回文串。
作者:jawhiow
链接:https://leetcode-cn.com/problems/palindromic-substrings/solution/liang-dao-hui-wen-zi-chuan-de-jie-fa-xiang-jie-zho/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution:
def countSubstrings(self, s: str) -> int:
n = len(s)
dp = [[0 for _ in range(n)] for _ in range(n) ]
count = 0
for i in range(n):
for j in range(i+1):
if i == j:
dp[i][j] = 1
count += 1
elif i - j == 1 and s[i] == s[j]:
dp[i][j] = 1
count += 1
elif i - j > 1 and s[i] == s[j] and dp[i-1][j+1]:
dp[i][j] = 1
count += 1
return count
买卖股票1
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
动态规划:
每天可以分为两种状态:持有股票或者不持有股票。
当持有股票是,可能是两种情况:
- 上一天持有,未抛出
- 今天购入
不持有股票,可能是两种情况:
- 上一天不持有,今天未购入
- 上一天持有,今天抛出
所有,对于股票[7,1,5,3,6,4]有如下dp
||||
|--|--|
|-7|0|
|-1|0|
|-1|4|
|-1|4|
|-1|5|
|-1|5|
动态转移方程为:
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][61] = max(dp[i-1][62], dp[i-1]+prices[i])
动态规划解法
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0] * 2 for _ in range(n)]
dp[0][0] = -prices[0]
dp[0][63] = 0
for i in range(1, n):
dp[i][0] = max(-prices[i], dp[i-1][0])
dp[i][64] = max(dp[i-1][65], dp[i-1][0]+prices[i])
return dp[-1][-1]
常规解法
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
min_value = max(prices)
max_value = 0
for i in range(n):
if prices[i] < min_value:
min_value = prices[i]
elif prices[i] - min_value > max_value:
max_value = prices[i] - min_value
return max_value
股票买卖 2
- 买卖股票的最佳时机 II
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
动态规划解法
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0] * 2 for _ in range(n)]
dp[0][0] = -prices[0]
dp[0][66] = 0
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][67]-prices[i])
dp[i][68] = max(dp[i-1][69], dp[i-1][0]+prices[i])
return dp[-1][-1]
常规解法:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
max_value = 0
for i in range(1, n):
if prices[i] > prices[i-1]:
max_value += (prices[i] - prices[i-1])
return max_value
动态规划小结
在上面的题目中题目多半是二维列表,所以动态规划也是二维列表的形式。而题目是一维列表的多半是一维列表能解决。二维列表的套路是,首先建立一个二维的dp列表,然后往dp列表中填值,最后计算出dp中的最大值。dp[i][j] 往往依赖于 dp[i-1][j] ,dp[i][j-1], dp[i][j]。
但是有一点需要仔细区别的是对于一个二维列表的题目想清楚使用动态规划还是二维列表的基本方法。就先是二维矩阵最大和子矩阵和最大正方形就很类似,但是前者是基础循环,后者是动态规划。