经典排序 python实现

 

 

 

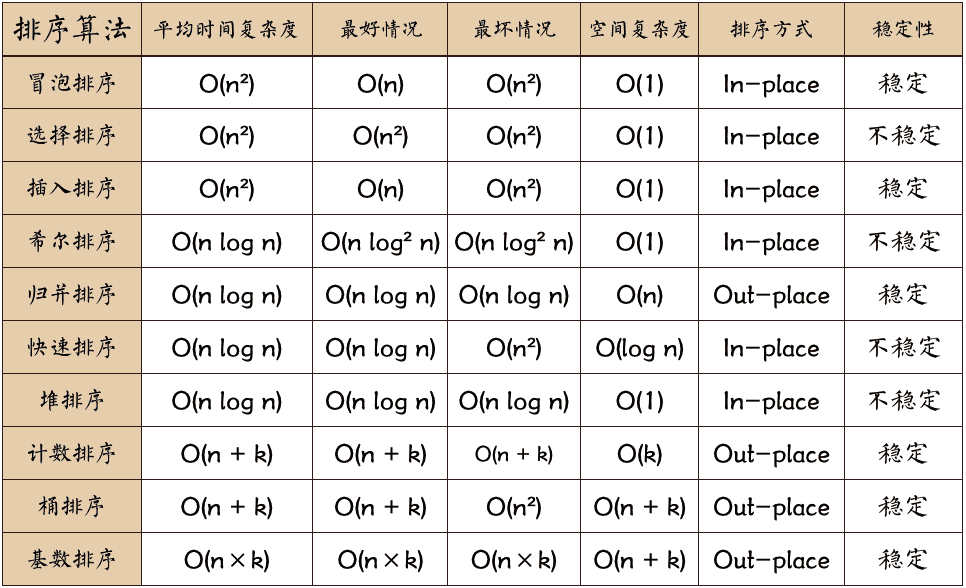
稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。 
不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

冒泡

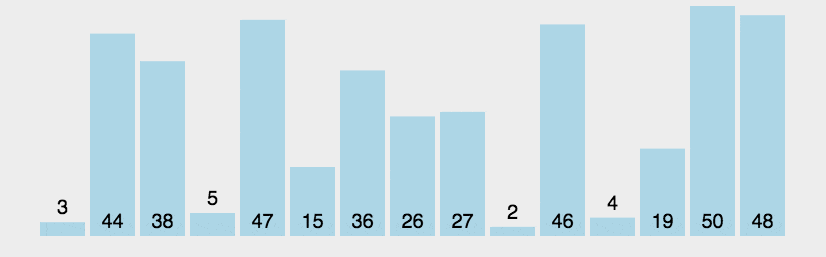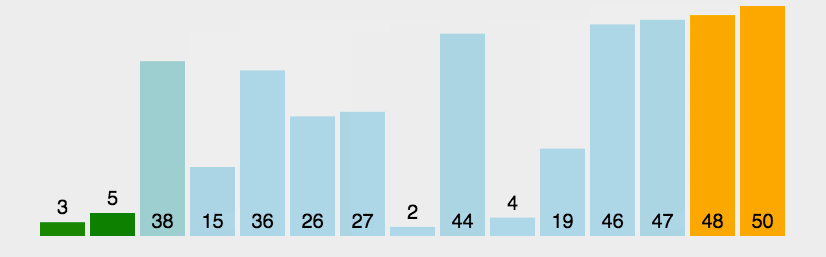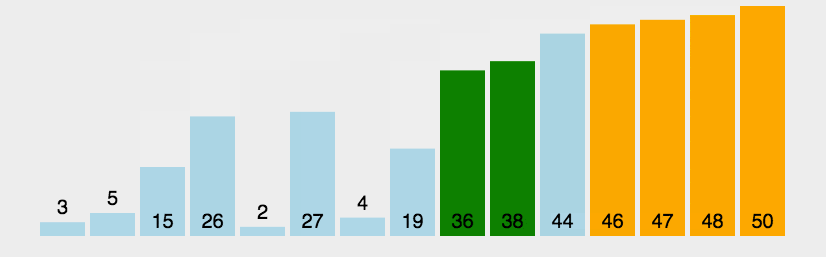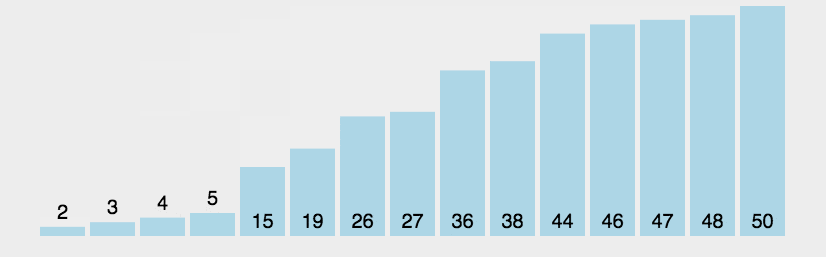
def bobble(arr):
    length = len(arr)
    for i in range(length):
        for j in range(length-i-1):
            if arr[j] > arr[j+1]:
                arr[j],arr[j+1] = arr[j+1],arr[j]

选择

选择排序的思想是将序列分为有序和无序两个部分，不断从无序序列中选择最小的增加到有序序列中，这样，序列就从小到大排列整齐。

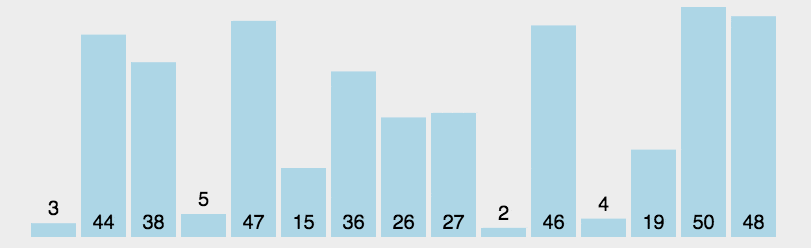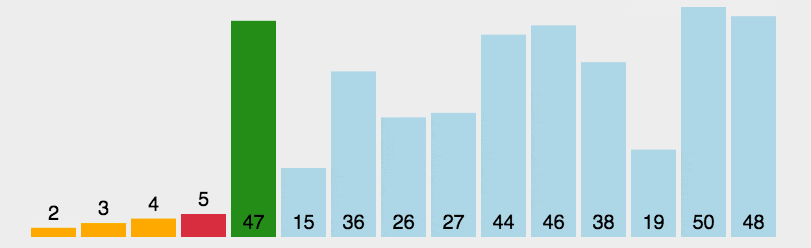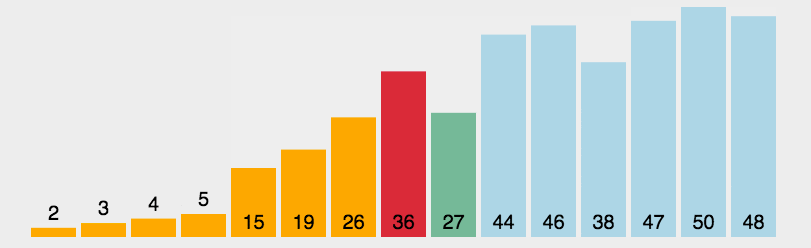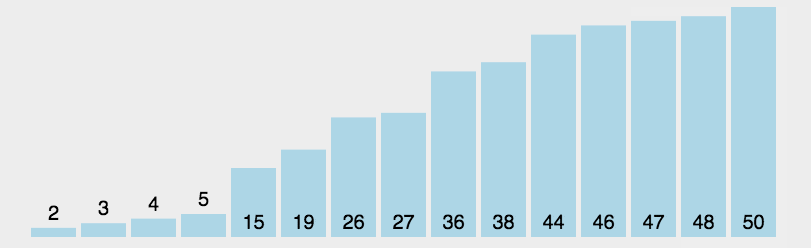
def select(arr):
    length = len(arr)
    for i in range(length):
         temp = arr[i]
         index = i 
         #该序列就是从无序序列中寻找最小的元素，然后加入到有序序列中。
         for j in range(i,length)
             if arr[j] < temp:
                 temp = arr[j]
                 index = j
         if i != index:
             arr[i],arr[index] = arr[index],arr[i]

插入排序

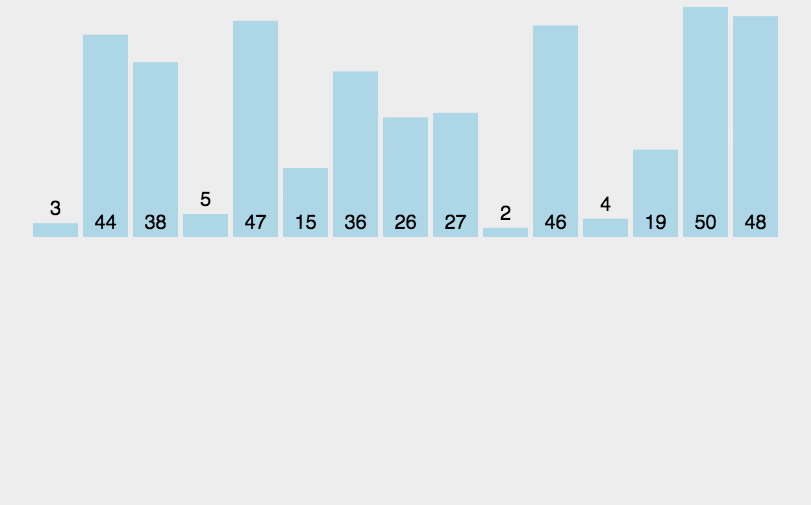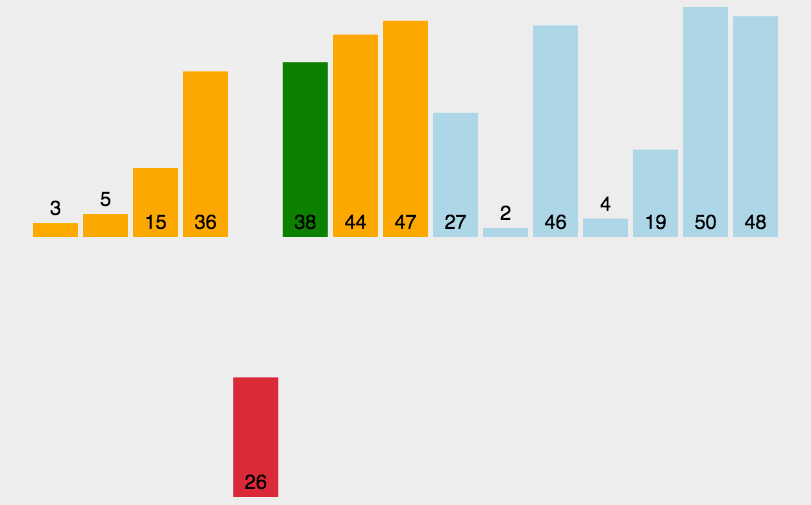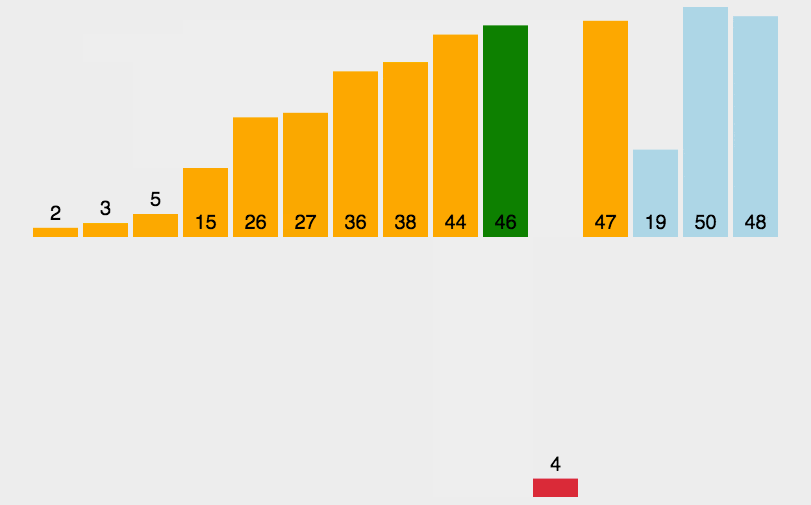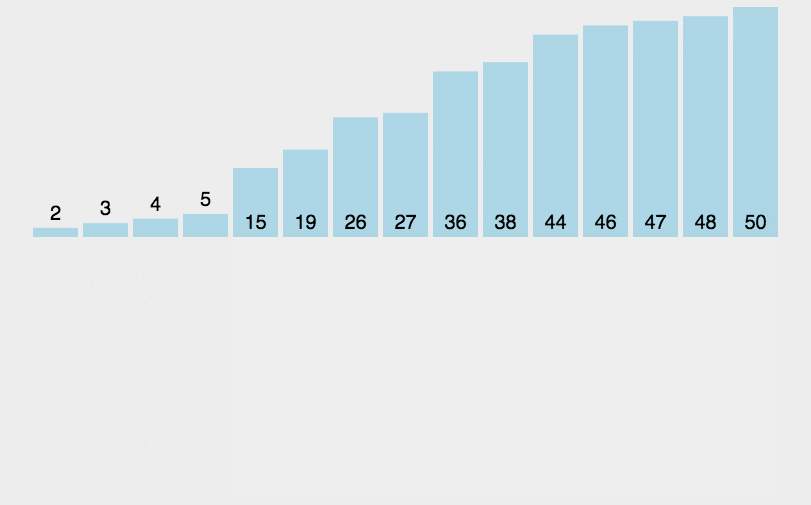
插入排序原理是将当前元素与前面的元素比较，如果小于则不断移动前面的元素向后，直到大于前面的某一个元素。

1.使用一个变量保存当前元素

2.使用变量不断与前面的元素比较，如果小于前面的变量则移动被比较的元素向后，直到变量大于某一个元素则停止

def insert_fun(arr):
    length = len(arr)
    for i in range(length):
        #使用temp将当前要排序的元素保存，以便后面操作
        temp = arr[i]
        preindex = i-1
        while arr[preindex] > temp and preindex >= 0:
            arr[preindex+1] = arr[preindex]
            preindex = preindex - 1
        '''
        有两种情况退出循环，一是temp大于前面某一个元素，这时要将temp插入该元素的后面；二是preindex小于0，能到这里temp肯定是小于前面所有的元素的，所以最后preindex = -1，temp是最小的元素，所以插入在第一个元素里
        '''
        arr[preindex+1] = temp

希尔排序

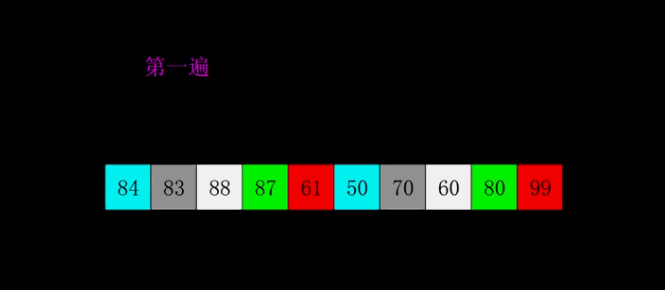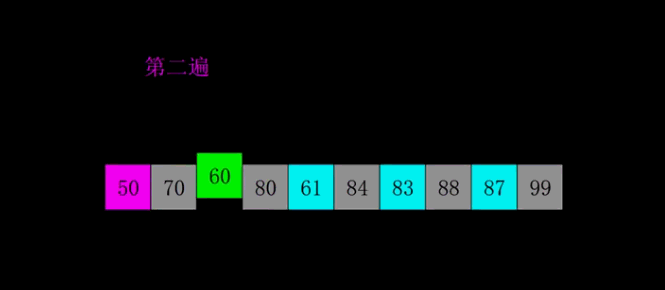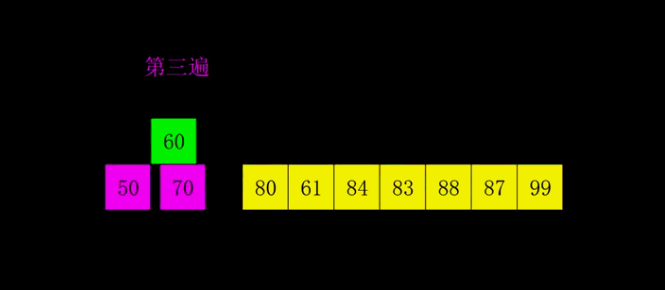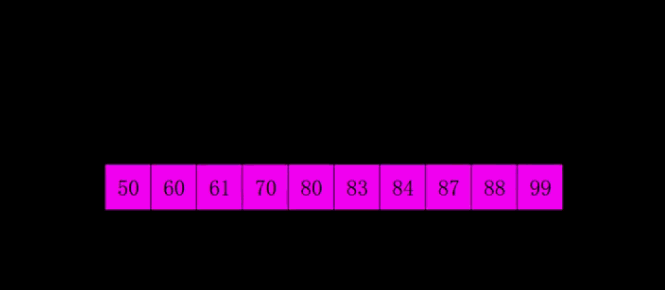
因为插入排序效率在集合大体有序时比较高，所有希尔的思想就是将数组先大体排序程成有序的状态。

gap是增量，使用增量将整体数组分割成若干小数组，先对小数组排序。直到gap=1，就变成了插入排序。

gap既是增量，又是大数组分割成小数组的数量。

希尔排序是插入排序的改进版，其改进之处在于希尔排序的最后一次排序就是插入排序，而在之前希尔排序将集合大致排序程有序的序列。

def shellsort(arr):
    length = len(arr)
    gap = length // 2
    while gap > 0:
        #循环从每一组的第二个元素开始，并不是排好一组之后才排下一组，而是所有的排序都是交替进行的
        for i in range(gap,length):
#标准的插入排序，唯一不同的是步长为gap
#-----------------------------------------------------------
            temp = arr[i]
            preindex = i - gap
            while temp < arr[preindex] and preindex >= 0:
                arr[preindex+gap] = arr[preindex]
                preindex = preindex - gap
            arr[preindex+gap] = temp
#-----------------------------------------------------------
        gap = gap // 2

快速排序

https://www.cnblogs.com/morewindows/archive/2011/08/13/2137415.html 
快速排序的是思想是从序列中找一个元素作为基准，将所有小于基准的元素都排在前面，所有大于基准的元素都排在后面。此时序列就被分成两个部分，然后重复该过程，直到所有的序列都有序为止。

以上的思想是排序的思想，实际的代码思想应该用挖坑填坑，分而治之。

 

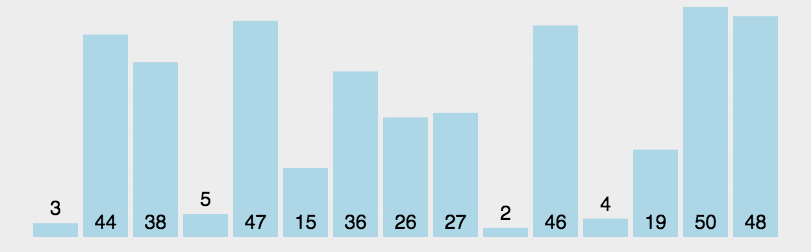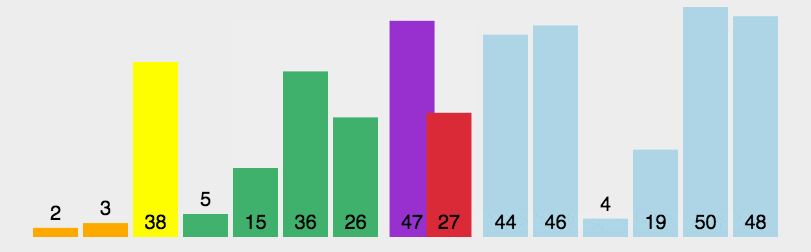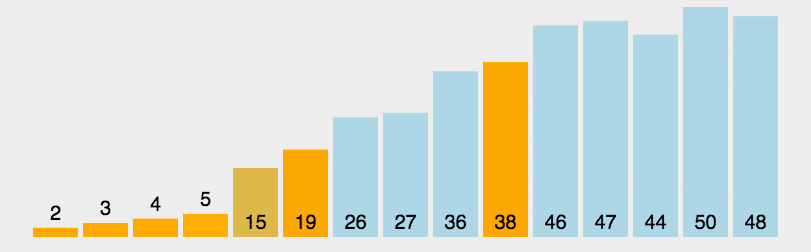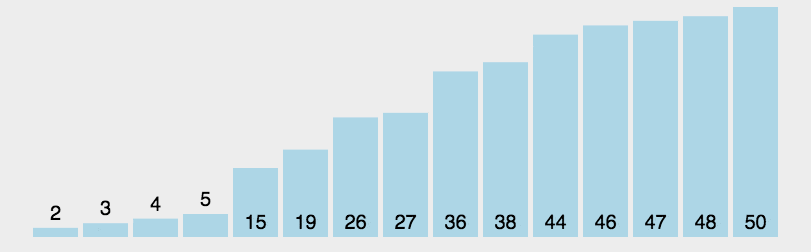
双循环法

#coding:utf-8
def quick(arr,left,right):
    temp = arr[left]
    while left < right:
        while left  < right and arr[right] >= temp:
            right = right - 1
        if left < right:
            arr[left] = arr[right]
            left = left + 1
        while left < right and arr[left] <= temp:
            left = left + 1
        if left < right:
            arr[right] = arr[left]
            right = right - 1
    arr[right] = temp
    return right
def fun(arr,left,right):
    if left < right:
        i = quick(arr,left,right)
        #递归调用，传入参数右边终点下标比上一次减少1，所以一定会有退出的时刻
        fun(arr,left,i-1)
        #递归调用，传入参数左边起点下标比上一次增加1，所以一定会有退出的时刻
        fun(arr,i+1,right)
arr = [4,3,10,58,88,23,22,98,8,9,10]
fun(arr,0,len(arr)-1)
print arr

单循环法 

def quick(array,left,right):
     
    if left < right:
        # mid = quick_sort(array,left,right)
        temp = array[left]
        mark = left
        for i in range(left+1,right+1):
            if temp > array[i]:
                mark = mark + 1
                array[mark],array[i] = array[i],array[mark]

        array[mark],array[left] = array[left],array[mark]
        # return mark
        quick(array,left,mark-1)
        quick(array,mark+1,right)

  

归并排序

https://www.cnblogs.com/piperck/p/6030122.html 
归并排序思想：先并开，后归拢。将一个序列中所有元素都分开，然后从单个元素开始两两合并，将两个有序序列合并成一个新的序列。

 

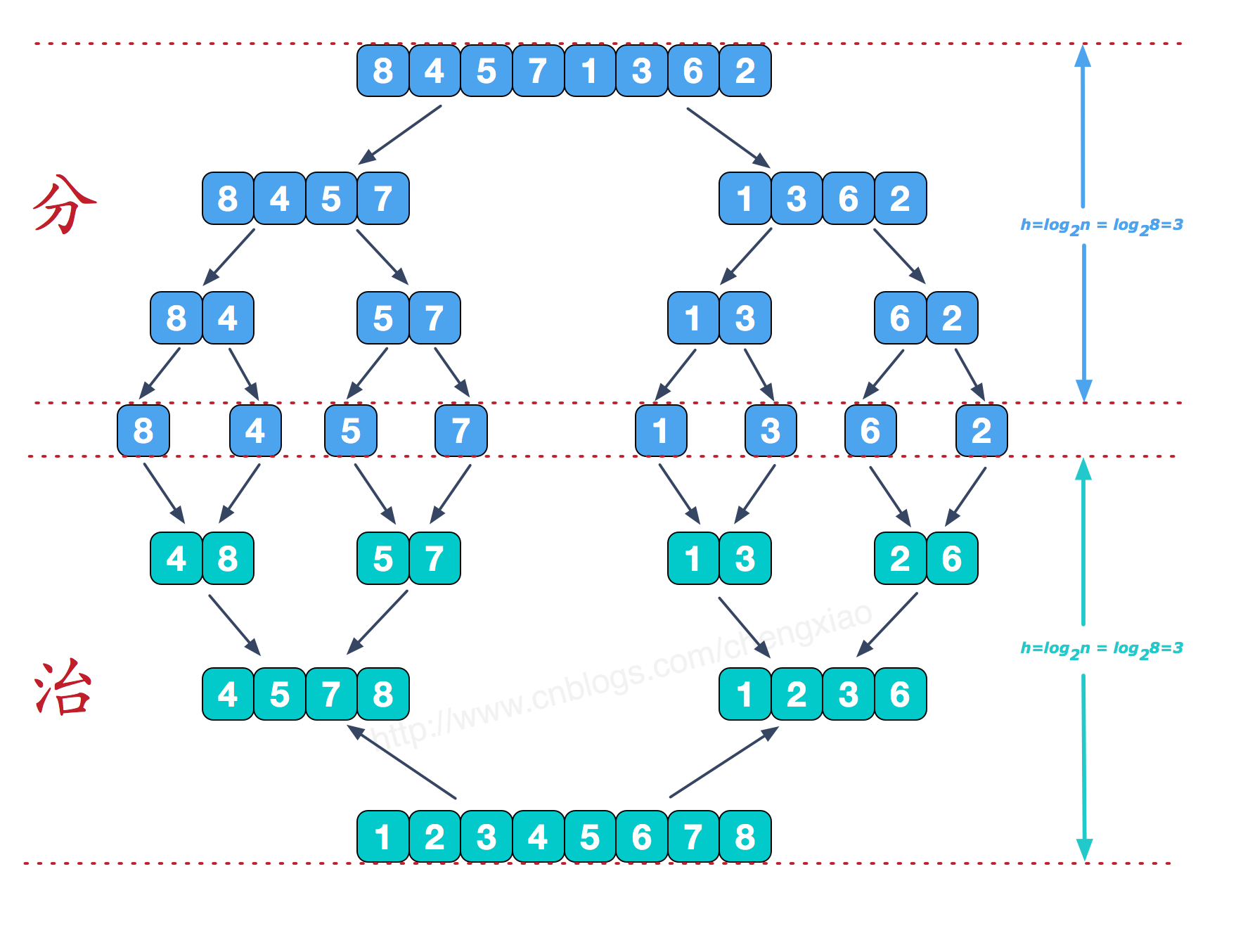
def merge_sort(left,right):
          
    l = 0
    r = 0
    temp = []

    while l < len(left) and r < len(right):

        if left[l] < right[r]:
            temp.append(left[l])
            l = l + 1
        else:
            temp.append(right[r])
            r = r + 1

    if l == len(left):
        temp.extend(right[r:])
    else:
        temp.extend(left[l:])

    return temp

def merge(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    #并的过程，将一个完整的序列分成单个元素，当arr=1时，说明序列被分成很多个单个元素
    left = merge(arr[:mid])
    right = merge(arr[mid:])
    #归的过程。将序列两两合并，然后递归完成这个过程，最后到所有的递归完成，序列重新完整，但此时序列已经完成排序。
    return merge_sort(left,right)

num_list = [34,2,8,98,72,44,84,11,49,28,34,87,45,23,99,100]
result = merge(num_list)
print(result)

计数排序

http://www.sohu.com/a/258222713_684445

计数排序是一个种外排序，需要一个数组的辅助。排序思想是：

1.首先求出待排序的集合中的最大值

2.然后根据最大值建立max+1个元素的列表

3.将待排序元素的值和列表的下标一一对应，有元素的值就在列表对应的下标的元素加1

4.所有元素对应完成，此时列表就表示排好序的集合，顺序输出即可

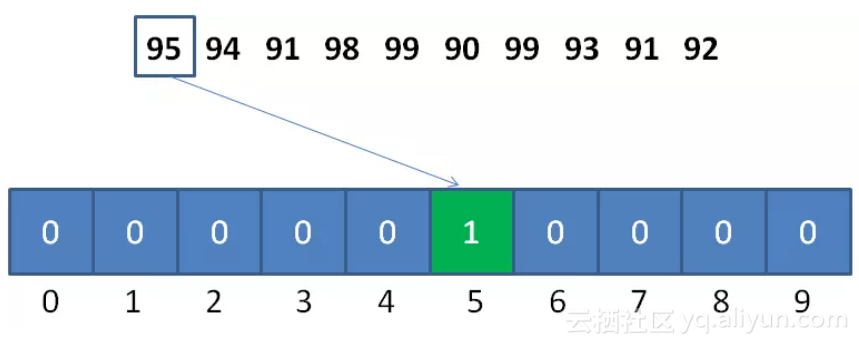
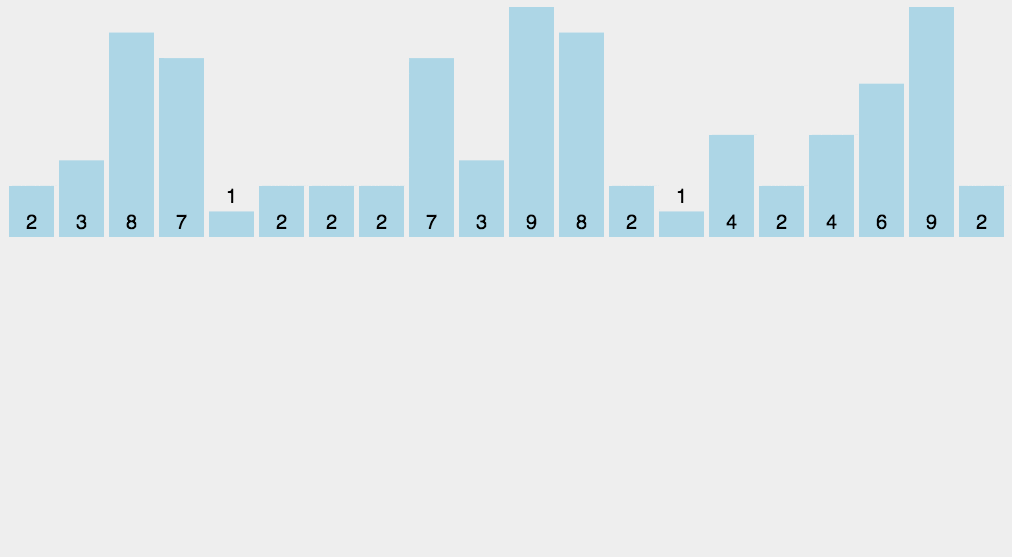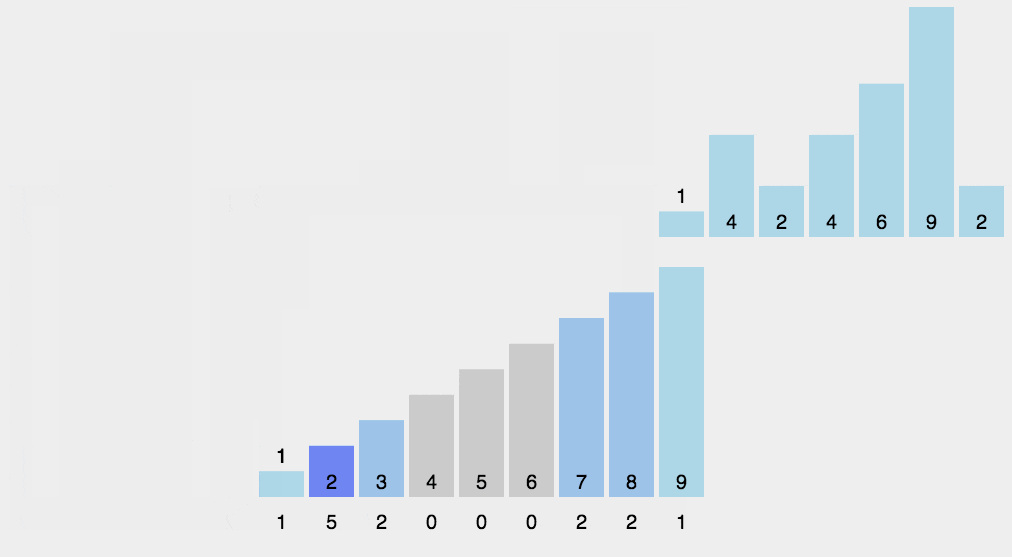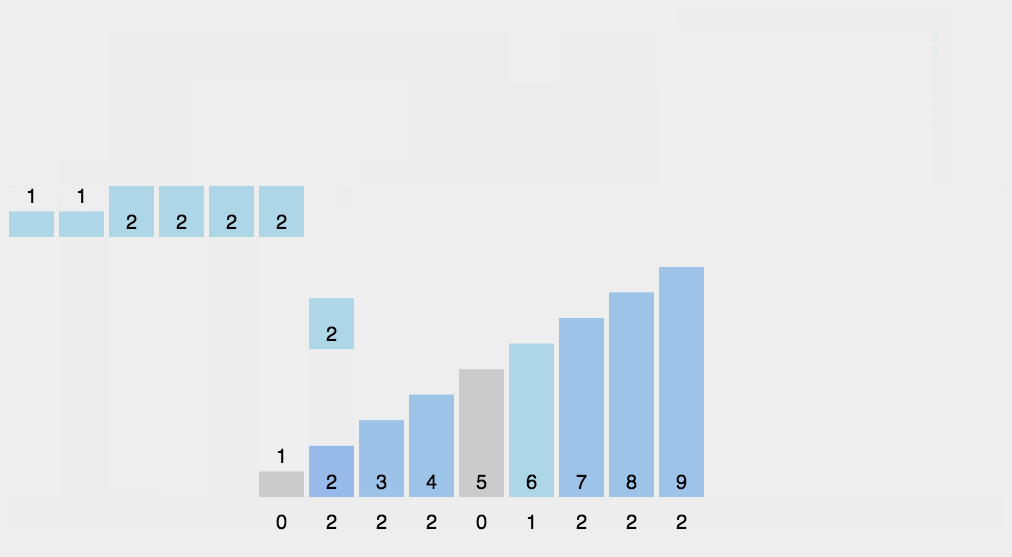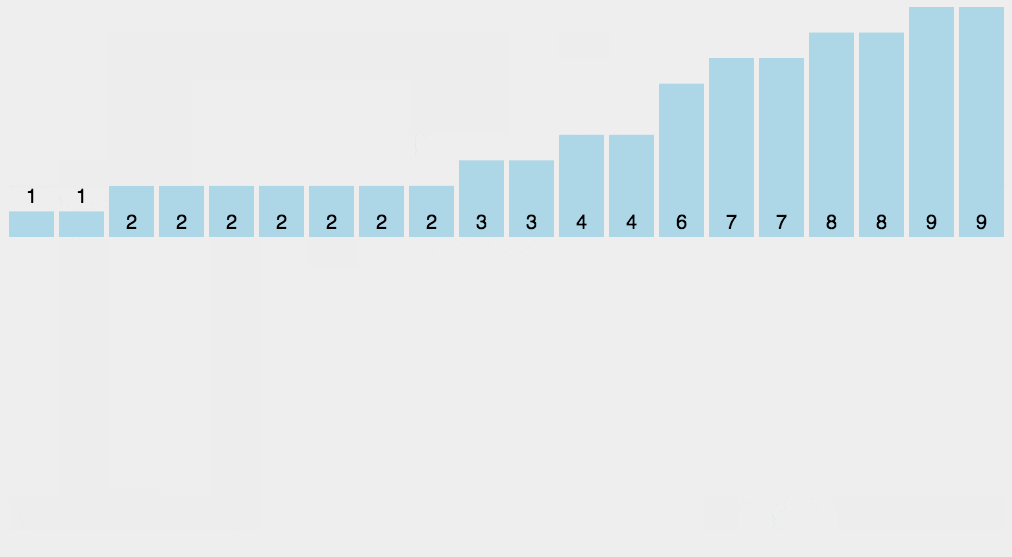
def countingsort(arr):
    max_value = max(arr)
    length = max_value + 1
    temp = [0] * length
    coll = []
    for i in arr:
        temp[i] = temp[i] + 1
    for j in range(len(temp)):
        index = temp[j]
        while index > 0:
            coll.append(j)
            index = index - 1
    return coll

桶排

https://yq.aliyun.com/articles/652774

桶排序是计数排序的优化版。计数排序的思想是构建一个列表，其长度是待排序集合的最大值+1。这样当集合过大时，资源浪费。

通排序是用一个列表当做一个桶，代表一个取值范围。节省了创建的列表的数量。排序思想：

1.首先找出最大值，根据最大值确定桶的数量

2.将所有的元素放入对应的桶中

3.对每个桶进行快速排序，结束后桶内有序，并且所有的桶组合在一def quick(    l = lef    r = right

if left < right:
        temp =  arr[left]
        while left < right:
            while left < right and temp < arr[right]:
                right = right - 1
            if left < right:
                arr[left] = arr[right]
                left  = left + 1
            while left < right and temp > arr[left]:
                left = left + 1
            if left < right:
                arr[right]  = arr[left]
                right = right - 1
        arr[left] = temp
        index = left  
        quick(arr,l,index-1)
        quick(arr,index+1,r)
def quicksort(arr):
    max_index = len(arr) - 1
    quick(arr,0,max_index)
def bucket(arr):
    n = len(arr)
    max_num = max(arr)
    num = max_num // 10 + 1
    buckets = [[] for i in range(num)]
    coll = []
    for i in arr:
        buckets[i//10].append(i)
    for bucket in buckets:
        quicksort(bucket)
    for bucket in buckets:
        if bucket:
            coll.extend(bucket)
return coll

基数排序

https://cuijiahua.com/blog/2018/01/algorithm_8.html

 基数排序的思想比较有创意，按照每一个元素的位排序。先按照个位将集合排序，然后再用十位将上次排好的集合再排序，直到最高位的元素都排好。

1.找出最大的位数

2.循环取出每个元素的个位，按照个位的值放入一个0~9的桶中

3.循环上一个过程，位数不断变高

4.最后输出即一个有序的集合

def radix(arr):
    digit = 0
    max_digit = 1
    max_value = max(arr)
    while 10 ** max_digit < max_value:
        max_digit = max_digit + 1
    while digit < max_digit:
        buckets = [[] for x in range(10)]
        for i in arr:
            t = int((i/10**digit)%10)
            buckets[t].append(i)
        coll = []
        for bucket in buckets:
            coll.extend(bucket)
        digit = digit + 1
        arr = coll
    return coll

堆排

https://www.jianshu.com/p/938789fde325

 

堆排序又叫做二叉堆排序 
二叉堆是一种完全二叉树，它的类型分为两种： 
1. 最大堆 
2. 最小堆

 

最大堆：任何一个父节点，都大于或等于它左孩子和右孩子节点的值

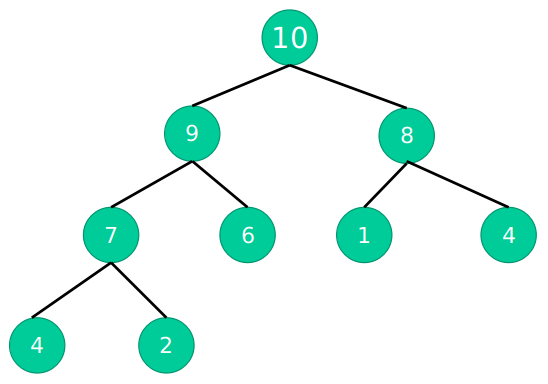
 最小堆：任何一个父节点，都小于或等于它左孩子和右孩子节点的值 

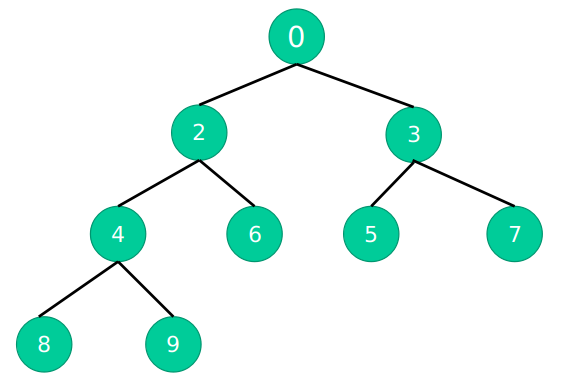
堆排序有两个步骤：
1. 将一个无序的数组排列成有序的堆
2. 不断将堆顶节点和最后一个节点互换，然后平衡二叉堆

# 元素下沉，可以将无序的堆调成成有序堆
def down_adjust(parent_index, length, array=[]):
    #temp = array[parent_index]
    child_index = 2 * parent_index + 1
    while child_index < length:
        if child_index + 1 < length and array[child_index+1] < array[child_index]:
            child_index += 1
          if temp < array[child_index]:
            break

        #array[parent_index] = array[child_index]
          array[parent_index],array[child_index] = array[child_index],array[parent_index]
        parent_index = child_index
        child_index = 2 * parent_index + 1
    #array[parent_index] = temp

def build_heap(array=[]):
    
    # 首先将无序的堆调成有序的堆
    for i in range((len(array)-2)//2, -1, -1):
        down_adjust(i, len(array), array)
    
    # 不断将堆的第一个元素和最后一个元素互换，然后调整堆
    for i in range(len(array)-1,0,-1):
        array[i],array[0] = array[0],array[i]
        down_adjust(0,i,array)

my_array = [7,1,3,10,5,2,8,9,6]
build_heap(my_array)
print(my_array)