微分中值定理:
罗尔定理([a,b]连续,(a,b)可导,f(a)=f(b) ,则f(x)在(a,b)中有一点的导数为0)
拉格朗日中值定理([a,b]连续,(a,b)可导,则f(x)在(a,b)中有一点的导数等于点A(a,f(a))和点B(b,f(b))的连线的斜率)
柯西中值定理 (把拉格朗日中值定理用参数方程的形式表达)
积分中值定理:
第一积分中值定理:

按几何意义来考虑:f(x)的积分为曲线与x=a,x=b,x轴围城的图形的面积。而等式右侧显然也是另外一种表达方式。
第二积分中值定理:

按第一部分来看因为g(x)>=0 且单调减,所以g(a)> g(b). 若在被积函数中提出一个g(a)得到的值必定大于原积分,所以要相等必须缩减积分限。
推论:
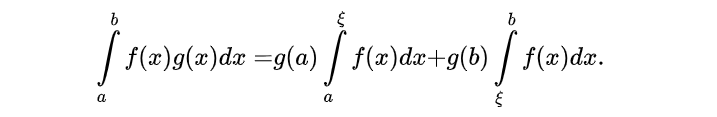
证明:
只需要证明g为单调递减函数即可,单调递增时同理
令 h(x)=g(x) - g(b)
h(x)也单调递减,可直接用定理得到h(x)f(x)为被积函数的一个等式,再把h(x)由g(x)-g(b)代入就可证明。