poj3334(Connected Gheeves)

Connected Gheeves

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1008		Accepted: 368

Description

Gheeves (plural of gheef) are some objects similar to funnels. We define a gheef as a two dimensional object specified by a sequence of points (p₁, p₂, ..., p_n) with the following conditions:

• 3 ≤ n ≤ 1000
• If a point p_i is specified by the coordinates (x_i, y_i), there is an index 1 < c < n such that y₁ > y₂ > ... > y_c and yc < y_c+1 < y_c+2 < ... < y_n. p_c is called the cusp of the gheef.
• For all 1 ≤ i < c, x_i < x_c and for all c < i ≤ n, x_i > x_c.
• For 1 < i < c, the amount of rotation required to rotate p_i-1 around p_i in clockwise direction to become co-linear with p_i and p_i+1, is greater than 180 degrees. Likewise, for c < i < n, the amount of rotation required to rotate p_i-1 around p_i in clockwise rotation to become co-linear with p_i and p_i+1, is greater than 180 degrees.
• The set of segments joining two consecutive points of the sequence intersect only in their endpoints.

For example, the following figure shows a gheef of six points with c = 4:

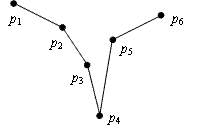
We call the sequence of segments (p₁p₂, p₂p₃, ..., p_n-1p_n), the body of the gheef. In this problem, we are given two gheeves P = (p₁, p₂, ..., p_n) and Q = (q₁, q₂, ..., q_m), such that all x coordinates of p_i are negative integers and all x coordinates of qi are positive integers. Assuming the cusps of the two gheeves are connected with a narrow pipe, we pour a certain amount of water inside the gheeves. As we pour water, the gheeves are filled upwards according to known physical laws (the level of water in two gheeves remains the same). Note that in the gheef P, if the level of water reaches min(y₁, y_n), the water pours out of the gheef (the same is true for the gheef Q). Your program must determine the level of water in the two gheeves after pouring a certain amount of water. Since we have defined our problem in two dimensions, the amount of water is measured in terms of area it fills. Note that the volume of pipe connecting cusps is considered as zero.

Input

The first number in the input line, t is the number of test cases. Each test case is specified on three lines of input. The first line contains a single integer a (1 ≤ a ≤ 100000) which specifies the amount of water poured into two gheeves. The next two lines specify the two gheeves P and Q respectively, each of the form k x₁ y₁ x₂ y₂ ... x_k y_k where k is the number of points in the gheef (n for P and m for Q), and the x_iy_i sequence specify the coordinates of the points in the sequences.

Output

The output contains t lines, each corresponding to an input test case in that order. The output line contains a single integer L indicating the final level of water, expressed in terms of y coordinates rounded to three digits after decimal points.
　

Sample Input

2
25
3 -30 10 -20 0 -10 10
3 10 10 20 0 30 10
25
3 -30 -10 -20 -20 -10 -10
3 10 10 20 0 30 10

Sample Output

3.536
-15.000

Source

Tehran 2006 Preliminary

 

 

 

题意：给定两个凹形的水槽，一个在y轴左半边，一个在右半边。水槽有个最低点，其中最低点左半边y坐标严格递减，右半边严格递增。两个水槽最低点有水管相连。给你a升水，全部灌入水槽后，水面高度为多少？

题解：二分最终高度，判断面积与a大小关系即可。怎么算高度为h时的面积呢？对于每个水槽，找出y=h与水槽边界两个交点，然后与y=h下方的顶点组成一个多边形，叉积算面积即可。

#include <bits/stdc++.h>
using namespace std;

const int inf = 0x3f3f3f3f;
const double eps = 1e-8;
const double pi = acos(-1.0);
const int maxn = 1010;

int cmp(double x) {
    if (fabs(x) < eps) return 0;
    if (x > 0) return 1;
    return -1;
}

inline double sqr(double x) {
    return x*x;
}

struct point {
    double x, y;
    point() {}
    point(double a, double b) : x(a), y(b) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    friend point operator + (const point& a, const point& b) {
        return point(a.x+b.x, a.y+b.y);
    }
    friend point operator - (const point& a, const point& b) {
        return point(a.x-b.x, a.y-b.y);
    }
    friend bool operator == (const point& a, const point& b) {
        return cmp(a.x-b.x)==0 && cmp(a.y-b.y)==0;
    }
    friend point operator * (const point& a, const double& b) {
        return point(a.x*b, a.y*b);
    }
    friend point operator * (const double& a, const point& b) {
        return point(a*b.x, a*b.y);
    }
    friend point operator / (const point& a, const double& b) {
        return point(a.x/b, a.y/b);
    }
    double norm() {
        return sqrt(sqr(x)+sqr(y));
    }
};

double det(const point& a, const point& b) {
    return a.x*b.y-a.y*b.x;
}

double calv(double h, vector<point>& p, int np, int lp) {
    int i = 0, j = np-1;
    double v = 0;
    while (i <= lp && p[i].y > h) ++i;
    while (j >= lp && p[j].y > h) --j;
    if (i <= j) {
        point c = point{p[i].x-(p[i].x-p[i-1].x)*(h-p[i].y)/(p[i-1].y-p[i].y), h};
        point d = point{p[j].x+(p[j+1].x-p[j].x)*(h-p[j].y)/(p[j+1].y-p[j].y), h};
        for (int k = i; k < j; ++k)
            v += det(p[k], p[k+1]);
        v += det(p[j], d) + det(d, c) + det(c, p[i]);
    }
    return fabs(v/2);
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        int np, nq, lp, lq;
        vector<point> p(maxn), q(maxn);
        double a;
        scanf("%lf", &a);
        lp = lq = 0;
        scanf("%d", &np);
        for (int i = 0; i < np; ++i) {
            p[i].input();
            if (p[i].y < p[lp].y)
                lp = i;
        }
        scanf("%d", &nq);
        for (int i = 0; i < nq; ++i) {
            q[i].input();
            if (q[i].y < q[lq].y)
                lq = i;
        }
        double l = min(p[lp].y, q[lq].y), r = (double)inf;
        r = min(p[0].y, min(p[np-1].y, min(q[0].y, q[nq-1].y)));
        while (fabs(r-l) > eps) {
            double m = (l + r) / 2;
            double v = calv(m, p, np, lp) + calv(m, q, nq, lq);
            if (cmp(v-a) >= 0) {
                r = m;
            } else {
                l = m;
            }
        }
        printf("%.3f
", r);
    }
    return 0;
}