很高兴能和大家一起共同学习算法导论这本书。笔者将在业余时间把算法导论后面的题解以博文的形式展现出来希望能得到大家的支持谢谢。如果有可能我会做一些教学视频免费的供大家观看。
练习题选自算法导论中文第三版第6页中的练习。
1.1-1 给出现实生活中需要排序的一个例子或者现实生活中需要计算凸壳的一个例子。
这个问题有俩个子问题。我一一解答:
(1) 首先是排序,日常需要排序的地方很多,例如今日微博热搜等等这个不用细说了。
(2)但是关于第二个问题我需要多写一点。
第一这本书的翻译的地方有误,凸壳在这里指的是计算几何中的多边形凸包问题。
下面摘选自百度百科。
⒈对于一个集合D,D中任意有限个点的凸组合的全体称为D的凸包。
⒉对于一个集合D,所有包含D的凸集之交称为D的凸包。
可以证明,上述两种定义是等价的
概念
示例图(一)
示例图(一)
1 点集Q的凸包(convex hull)是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内。右图中由红色线段表示的多边形就是点集Q={p0,p1,...p12}的凸包。
2 一组平面上的点,求一个包含所有点的最小的凸多边形,这就是凸包问题了。这可以形象地想成这样:在地上放置一些不可移动的木桩,用一根绳子把他们尽量紧地圈起来,并且为凸边形,这就是凸包了。
数学定义:设S为欧几里得空间 的任意子集。包含S的最小凸集称为S的凸包,记作conv(S)

凸包问题在实际中的应用很广泛,它可以应用于冶金术、城市规划、图像处理、统计学等等多个领域。
1.1-2 除速度外,在真实环境中还可能使用哪些其他有关效率的量度?
学过高中物理的都知道有功率吧。实际生产中还有开发效率,生产效率。
别的笔者暂时也想不出来。
1.1-3 选择一种你以前已知的数据结构并讨论其优势和局限。
笔者在这里列举一个图的数据结构-------邻接矩阵。并以PAT练习平台中的某一道题来举例子。
首先介绍一下邻接矩阵:(图画的不咋好请谅解)

在这里 我们完全可以用一个矩阵来将右边的无向图的节点和节点之间的关系完美的表现出来,但是当我们的节点过多,而关系少的时候,这个邻接矩阵就显得过于臃肿了,所以我们可以总结出以下俩点:
1)邻接矩阵的优势在于描述通俗易懂,算法实现起来简单,在稠密矩阵中效率依然很高。
2)邻接矩阵的局限性在于在处理的节点过多的时候(即稀疏矩阵),无论是时间复杂度还是空间复杂度均过高。
下面这道题是一道练手的简单题,有兴趣的朋友可以去做一下来感受一下邻接矩阵和稀疏矩阵的不同。
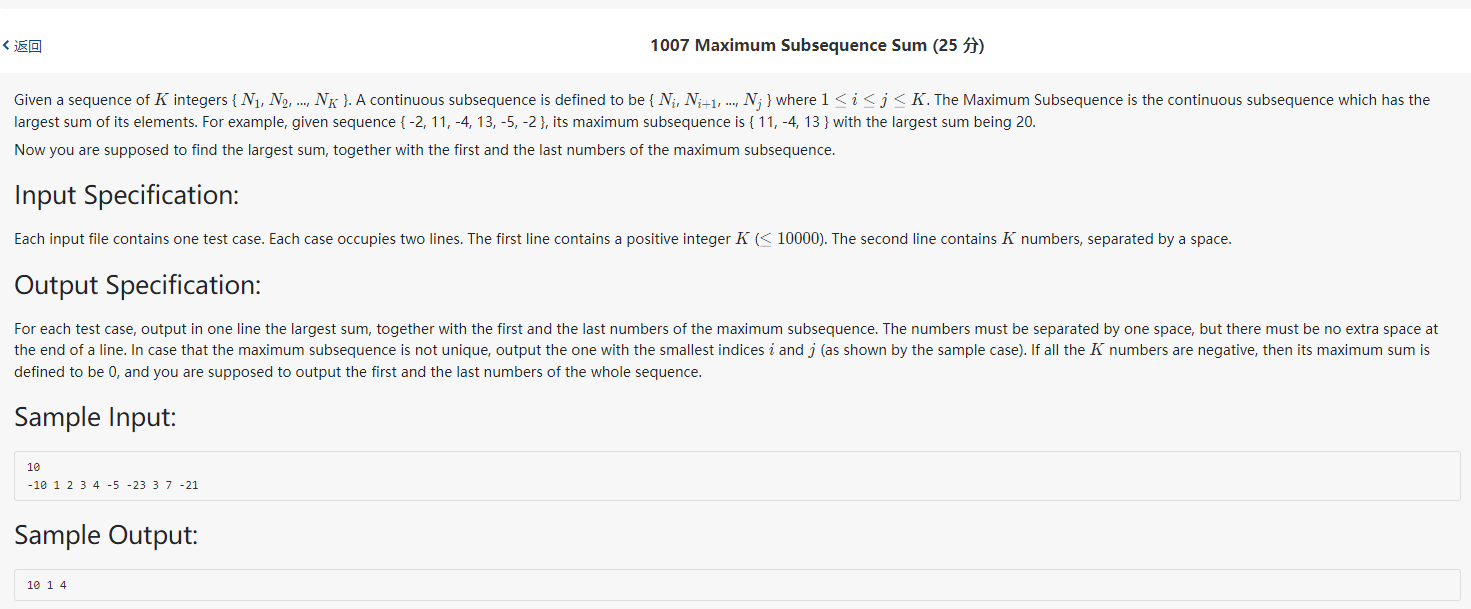
这道题如果你认真的去做了,你就会发现。虽然邻接矩阵无论是在算法实现上还是结构都很简单,但是无论如何也不能避免他在遍历的时候的时间复杂度过高,(一般都是O^2级别)。
因此一般在处理稀疏矩阵的时候,我们一般选择邻接表的实现方法去替代邻接矩阵的实现方法。
1.1-4 前面给出的最短路径与旅行商问题有哪些相似之处又有哪些不同?
旅行商问题简而言之就是选出所有可能的候选路径,而非最短路径。
它们是相似的,因为每个人都必须走一个图并在其中找到一条路径。
他们又是不同的,最短路径仅需要两点之间的路径,而旅行推销员需要在返回第一点的更多点之间的路径。
至于如何寻找最短路径最简单的方法就是进行BFS(宽度优先遍历)。
下面是摘取百度百科的介绍
已知图G=(V,E)和一个源顶点s,宽度优先搜索以一种系统的方式探寻G的边,从而“发现”s所能到达的所有顶点,并计算s到所有这些顶点的距离(最少边数),该算法同时能生成一棵根为s且包括所有可达顶点的宽度优先树。对从s可达的任意顶点v,宽度优先树中从s到v的路径对应于图G中从s到v的最短路径,即包含最小边数的路径。该算法对有向图和无向图同样适用。
之所以称之为宽度优先算法,是因为算法自始至终一直通过已找到和未找到顶点之间的边界向外扩展,就是说,算法首先搜索和s距离为k的所有顶点,然后再去搜索和S距离为k+l的其他顶点。
通俗点说,就是在每一次遍历的时候,将每个子节点放入一个队列中,然后再不断递归以此寻找最短路径。
对于最短路径的寻找方法还有俩种最经典的。
1)Dijkstra(迪杰斯特拉)算法
他的算法思想是按路径长度递增的次序一步一步并入来求取,是贪心算法的一个应用,用来解决单源点到其余顶点的最短路径问题。
算法思想
首先,我们引入一个辅助向量D,它的每个分量D[i]表示当前找到的从起始节点v到终点节点vi的最短路径的长度。它的初始态为:若从节点v到节点vi有弧,则D[i]为弧上的权值,否则D[i]为∞,显然,长度为D[j] = Min{D[i] | vi ∈V}的路径就是从v出发最短的一条路径,路径为(v, vi)。
那么,下一条长度次短的最短路径是哪一条呢?假设次短路径的终点是vk,则可想而知,这条路径或者是(v, vk)或者是(v, vj, vk)。它的长度或者是从v到vk的弧上的权值,或者是D[j]和从vj到vk的权值之和。
一般情况下,假设S为已知求得的最短路径的终点集合,则可证明:一下条最短路径(设其终点为x)或者是弧(v, x)或者是中间只经过S中的顶点而最后到达顶点x的路径。这可用反证法来证明,假设此路径上有一个顶点不在S中,则说明存在一条终点不在S中而长度比此路径短的路径。但是这是不可能的。因为,我们是按路径常度的递增次序来产生个最短路径的,故长度比此路径端的所有路径均已产生,他们的终点必定在S集合中,即假设不成立。
因此下一条次短的最短路径的长度是:D[j] = Min{D[i] | vi ∈ V - S},其中,D[i]或者是弧(v, vi)的权值,或者是D[k](vk ∈ S)和弧(vk, vi)上权值之和。
2)Floyd(弗洛伊德)算法
Floyd算法是一个经典的动态规划算法。是解决任意两点间的最短路径(称为多源最短路径问题)的一种算法,可以正确处理有向图或负权的最短路径问题。(动态规划算法是通过拆分问题规模,并定义问题状态与状态的关系,使得问题能够以递推(分治)的方式去解决,最终合并各个拆分的小问题的解为整个问题的解。)
算法思想
从任意节点i到任意节点j的最短路径不外乎2种可能:1)直接从节点i到节点j,2)从节点i经过若干个节点k到节点j。所以,我们假设arcs(i,j)为节点i到节点j的最短路径的距离,对于每一个节点k,我们检查arcs(i,k) + arcs(k,j) < arcs(i,j)是否成立,如果成立,证明从节点i到节点k再到节点j的路径比节点i直接到节点j的路径短,我们便设置arcs(i,j) = arcs(i,k) + arcs(k,j),这样一来,当我们遍历完所有节点k,arcs(i,j)中记录的便是节点i到节点j的最短路径的距离。(由于动态规划算法在执行过程中,需要保存大量的临时状态(即小问题的解),因此它天生适用于用矩阵来作为其数据结构,因此在本算法中,我们将不使用Guava-Graph结构,而采用邻接矩阵来作为本例的数据结构)