byte在计算机中的存储方式--Double.byteValue()的输出结果思考

先举三个栗子:

1.

public static void main(String[] args) {
        Double d = new Double(123.56);
        
        byte b = d.byteValue();
        
        System.out.println(b);
    }

输出结果:123

2.

public static void main(String[] args) {
        Double d = new Double(456.56);
        
        byte b = d.byteValue();
        
        System.out.println(b);
    }

输出结果:-56

3.

public static void main(String[] args) {
        Double d = new Double(567.56);
        
        byte b = d.byteValue();
        
        System.out.println(b);
    }

输出结果:55

大家应该看出来了吧,这三个只是Double的整数位变化了,但输出结果却差不少,而且一眼是看不出来规律的

原因解析:1.翻源码,看看byteValue()是咋处理的

上源码:

/**
     * Returns the value of this {@code Double} as a {@code byte}
     * after a narrowing primitive conversion.
     *
     * @return  the {@code double} value represented by this object
     *          converted to type {@code byte}
     * @jls 5.1.3 Narrowing Primitive Conversions
     * @since JDK1.1
     */
    public byte byteValue() {
        return (byte)value;
    }

惊不惊喜!意不意外!没错,就是强转了

2.Double强转byte时的操作过程

记住这句话:正整数在计算机中用原码来表示的，而负整数在计算机中用补码来表示的

1  取整

2  整数部分与[256]取模

3.1 如果该整数在[-128,127]之间,直接打印

3.2 如果该整数在[-128,127]之外,将这个值化为二进制,判断第一位是1还是0

　　3.2.1   如果是1,表明该数为一个负数

　　3.2.2   如果是0,表明该数为一个正数

好了,概念说完了,回头理解一下最开始举的栗子

先说第一个:

123.45  -->  取整  123  -->  整数部分与[256]取模  123  -->  在[-128,127]区间内  -->  打印输出

第一个最简单了,很容易理解,接下来讲第三个

注意啊,是第三个(因为第二个比较难,放在最后讲)

567.56  -->  取整  567  -->  整数部分与[256]取模  55  -->  在[-128,127]区间内  -->  打印输出

看,其实第一个和第三个是同样原理,接下来分析第二个

456.56  -->  取整  456  -->  整数部分与[256]取模  200  -->  在[-128,127]区间外

在区间外,所以我们将 200 转为二进制来看

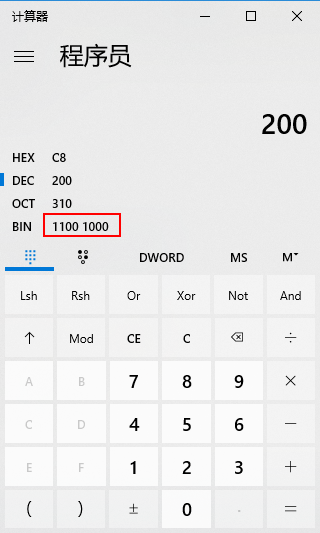
200二进制为 ‭1100 1000‬

第一位为1,也就是说这个数是个负数,还记得上面标粗体的让记住的那就话了么

记住这句话:正整数在计算机中用原码来表示的，而负整数在计算机中用补码来表示的

所以,这个 1100 1000‬ 其实存的是一个补码,我们根据补码算出原码

计算法则:

补码的补码就是原码

二、负整数的符号位固定为1，由原码变为补码时，规则如下：

      1、原码符号位1不变，整数的每一位二进制数位求反，得到反码

　　1011 0111

      2、反码符号位1不变，反码数值位最低位加1，得到补码

　　1011 1000

根据此数求出十进制的值

1*2^3 + 1*2^4 + 1*2^5 = 8 + 16 + 32 = 56

由于第一位为1,结果为负,即 -56

Double如果是负数也同样适用

声明:本文中未加粗的斜体摘自百度经验,其他原创手打,如需转载,请联系我本人