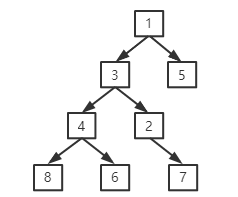
二叉树遍历如下图所示,前序遍历对于1(父),3(左),5(右)这三个节点来说则先1后3,最后5,同理3,4,2这三个也是先父再左再右,那么对于下图来说,前序遍历顺序为1,3,4,5,6,2,7,5,以此类推:
先序遍历:先父,再左,最后右,
中序遍历:先左,再父,最后右
后序遍历:先左,再右,最后父
我们先看递归版的前序遍历:
/** * 前序遍历 * @param head */ public static void preOrderRecur(Node head) { if (head == null) { return; } System.out.print(head.value + " "); preOrderRecur(head.left); preOrderRecur(head.right); }
代码非常简单,就是进来直接打印,然后先递归左子树,后递归右子树
/** * 中序遍历 * @param head */ public static void inOrderRecur(Node head) { if (head == null) { return; } inOrderRecur(head.left); System.out.print(head.value + " "); inOrderRecur(head.right); }
先递归左子树,然后打印,后递归右子树,相信看到这里,应该知道后序遍历咋写了“
/** * 后续遍历 * @param head */ public static void posOrderRecur(Node head) { if (head == null) { return; } posOrderRecur(head.left); posOrderRecur(head.right); System.out.print(head.value + " "); }
递归版的可以说是非常简单了,我们再来看下非递归版本怎么实现的:
/** * 前序遍历(非递归版) * @param head */ public static void preOrderUnRecur(Node head) { if(head != null){ Stack<Node> stack = new Stack<>(); stack.push(head); while(!stack.isEmpty()){ Node pop = stack.pop(); System.out.print(pop.value+ " "); if(pop.right != null){ stack.push(pop.right); } if(pop.left != null){ stack.push(pop.left); } } System.out.println(); } }
这里使用栈来存储节点,思想是循环先放入右节点,然后放入左节点,循环取出栈顶,这样可以每次循环先取出左节点,并且在打印时将左节点的右子节点放在当前节点的右节点上层,刚好满足我们的前序遍历,
再看中序遍历:
/** * 中序遍历 * @param head */ public static void inOrderUnRecur(Node head) { if(head != null) { Stack<Node> stack = new Stack<>(); while(!stack.empty() || head != null){ if(head != null){ stack.push(head); head = head.left; }else{ head = stack.pop(); System.out.print(head.value + " "); head = head.right; } } System.out.println(); } }
中序遍历非递归版本的思想:先将当前节点下所有非空左子节点塞入栈,出栈时打印并将右子节点放入栈,下一次循环打印,,则可以实现左,父,右的顺序打印。
后序遍历的难度稍微大点,因为我们前面打印的节点都是有直接关联的,比如左-父-右,这些都可以通过入栈出栈完成,而后序遍历为左-右-父,左右节点是没有直接联系的,所以我们没法通过出入栈去退栈打印,因此我们只能想其他办法去实现,比如:先序遍历的顺序为父-左-右,我们也可以改造一下变为父-右-左,反向打印不就是左-右-父了吗,说干就干:
/** * 后序遍历 * @param head */ public static void posOrderUnRecur(Node head) { System.out.print("pos-order: "); if(head != null){ Stack<Node> stack = new Stack<>(); Stack<Node> stack1 = new Stack<>(); stack.push(head); while(!stack.isEmpty()){ Node pop = stack.pop(); stack1.push(pop); if(pop.left != null){ stack.push(pop.left); } if(pop.right != null){ stack.push(pop.right); } } while(!stack1.empty()){ System.out.print(stack1.pop().value + " "); } } System.out.println(); }
这里我们对前序遍历进行了改造:将先入右再入左改为先入左再入右实现父-右-左的逆前序遍历,再将之前打印时改为入;另外一个栈,全部结束后出栈打印则可实现左-右-父的后序非递归打印,堪称完美。