什么是Re-ID?
- 行人重识别(Person re-identification,简称Re-ID)也称行人再识别,是利用计算机视觉技术判断图像或者视频序列中是否存在特定行人的技术。广泛被认为是一个图像检索的子问题。给定一个监控行人图像,检索跨设备下的该行人图像。旨在弥补目前固定的摄像头的视觉局限,并可与行人检测/行人跟踪技术相结合,可广泛应用于智能视频监控、智能安保等领域。
- 如下图所示:一个区域有多个摄像头拍摄视频序列,ReID的要求对一个摄像头下感兴趣的行人,检索到该行人在其他摄像头下出现的所有图片。

为什么要Re-ID?
在监控视频中,由于相机分辨率和拍摄角度的缘故,通常无法得到质量非常高的人脸图片。当人脸识别失效的情况下,ReID就成为了一个非常重要的替代品技术。
研究形式
- 数据集通常是通过人工标注或者检测算法得到的行人图片,目前与检测独立,注重识别
- 数据集分为训练集、验证集、Query、Gallery
- 在训练集上进行模型的训练,得到模型后对Query与Gallery中的图片提取特征计算相似度,对于每个Query在Gallery中找出前N个与其相似的图片
- 训练、测试中人物身份不重复

两大方向
- 特征提取:学习能够应对在不同摄像头下行人变化的特征
- 度量学习 :将学习到的特征映射到新的空间使相同的人更近不同的人更远
存在挑战
- 不同下摄像头造成行人外观的巨大变化;
- 目标遮挡(Occlusion)导致部分特征丢失;
- 不同的 View,Illumination 导致同一目标的特征差异;
- 不同目标衣服颜色近似、特征近似导致区分度下降;
常用数据集
CUHK03
Market1501
DukeMTMC-reID
MSMT17
这里只列举了常用的数据集,更全的数据集可以参考:Person Re-identification Datasets
常用评价指标
- rank-k:算法返回的排序列表中,前k位为存在检索目标则称为rank-k命中。eg:rank1:首位为检索目标则rank-1命中。
- Cumulative Match Characteristic (CMC)
举个很简单的例子,假如在人脸识别中,底库中有100个人,现在来了1个待识别的人脸(假如label为m1),与底库中的人脸比对后将底库中的人脸按照得分从高到低进行排序,我们发现:
如果识别结果是m1、m2、m3、m4、m5……,则此时rank-1的正确率为100%;rank-2的正确率也为100%;rank-5的正确率也为100%;
如果识别结果是m2、m1、m3、m4、m5……,则此时rank-1的正确率为0%;rank-2的正确率为100%;rank-5的正确率也为100%;
如果识别结果是m2、m3、m4、m5、m1……,则此时rank-1的正确率为0%;rank-2的正确率为0%;rank-5的正确率为100%;
同理,当待识别的人脸集合有很多时,则采取取平均值的做法。例如待识别人脸有3个(假如label为m1,m2,m3),同样对每一个人脸都有一个从高到低的得分,
比如:
人脸1结果为m1、m2、m3、m4、m5……,
人脸2结果为m2、m1、m3、m4、m5……,
人脸3结果m3、m1、m2、m4、m5……,
则此时rank-1的正确率为(1+1+1)/3=100%;
rank-2的正确率也为(1+1+1)/3=100%;
rank-5的正确率也为(1+1+1)/3=100%;
比如:
人脸1结果为m4、m2、m3、m5、m6……,
人脸2结果为m1、m2、m3、m4、m5……,
人脸3结果m3、m1、m2、m4、m5……,
则此时rank-1的正确率为(0+0+1)/3=33.33%;
rank-2的正确率为(0+1+1)/3=66.66%;
rank-5的正确率也为(0+1+1)/3=66.66%;
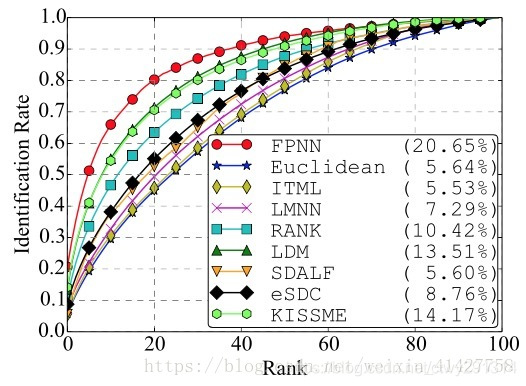
curve:计算rank-k的击中率,形成rank-acc的曲线,如下图:
- mAP(mean average precision):反应检索的人在数据库中所有正确的图片排在排序列表前面的程度,能更加全面的衡量ReID算法的性能。如下图,假设该检索行人在gallery中有10张图片,在检索的list中位置(rank)分别为1、2、3、4、5、6、7、8、9,则ap为(1/ 1 + 2 / 2 + 3 / 3 + 4 / 4 + 5 / 5 + 6 / 6 + 7 / 7 + 8 / 8 + 9 / 9) / 10 = 0.90;ap较大时,该行人的检索结果都相对靠前,对所有query的ap取平均值得到mAP

一般来说,Precision就是检索出来的条目(比如:文档、网页等)有多少是准确的,Recall就是所有准确的条目有多少被检索出来了。
正确率 = 检测出来的正样本数/检测出来的总数
召回率 = 检测出来的正样本数/所有正样本个数
我们来举一个新的例子。
假设有一个搜索引擎,根据搜索引擎,有如下结果:
搜索1相关的样本总共有5个: 正,正,正,正,正
| Rank1 | 正 | 负 | 正 | 负 | 负 | 正 | 负 | 负 | 正 | 正 |
|---|---|---|---|---|---|---|---|---|---|---|
| Recall | 1/5=0.2 | 1/5=0.2 | 2/5=0.4 | 2/5=0.4 | 2/5=0.4 | 3/5=0.6 | 3/5=0.6 | 3/5=0.6 | 4/5=0.8 | 5/5=1.0 |
| Precision | 1/1=1.0 | 1/2=0.5 | 2/3=0.66 | 2/4=0.5 | 2/5=0.4 | 3/6=0.5 | 3/7=0.42 | 3/8=0.38 | 4/9=0.44 | 7/10=0.5 |
Precision从左到右1/1, 1/2, 2/3, 2/4…以此类推
搜索2相关样本总共有3个,以下是搜索引擎返回的结果
| Rank1 | 正 | 负 | 负 | 正 | 正 | 负 | 负 |
|---|---|---|---|---|---|---|---|
| Recall | 0.33 | 0.33 | 0.33 | 0.66 | 1 | 1 | 1 |
| Precision | 1.0 | 0.5 | 0.33 | 0.5 | 0.6 | 0.5 | 0.43 |
我们把每个正样本所对应的Precision求平均
搜索1的mAP:mAP = (1/1 + 2/3 + 3/6 + 4/9+ 5/10) / 5 = 0.72
搜索2的mAP: mAP = (1/1 + 2/4 + 3/5) / 3 = 0.63
整体的mAP = (0.72 + 0.63) /2 = 0.675