牛客挑战赛44D-数列的和

题目描述

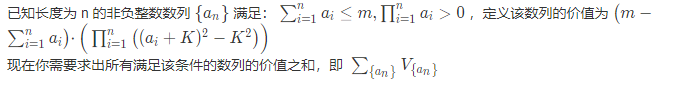
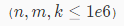
题解

因为换了题所以1h怒写exp然后跑不动

生成函数乱推即可

(ans=sum_{i=n}^{m}(m-i)[x^i](sum_{j>=1} j(j+2k)x^j)^n)

有(sum_i x^i=frac{1}{1-x})，(sum_i ix^i=frac{x}{(1-x)^2})，(sum_i i^2x^i=frac{2x}{(1-x)^3}-frac{x}{(1-x)^2})

代入到后面的提出(frac{1}{(1-x)^2})，二项式展开后交换ij，把生成函数换成组合数，发现求的是一列乘上m-i的值，简单转化即可

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define add(a,b) a=((a)+(b))%mod
#define mod 998244353
#define Mod 998244351
#define ll long long
#define N 4000000
//#define file
using namespace std;

ll jc[N+1],Jc[N+1],ans,Ans;
int n,m,K,i,j,k,l;

ll qpower(ll a,int b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}
ll C(int n,int m) {if (n<m) return 0;return jc[n]*Jc[m]%mod*Jc[n-m]%mod;}

int main()
{
	#ifdef file
	freopen("d.in","r",stdin);
	#endif
	
	jc[0]=1;
	fo(i,1,N) jc[i]=jc[i-1]*i%mod;
	Jc[N]=qpower(jc[N],Mod);
	fd(i,N-1,0) Jc[i]=Jc[i+1]*(i+1)%mod;
	
	scanf("%d%d%d",&n,&m,&K);
	if (n>m) {printf("0
");return 0;}
	fo(j,0,n)
	{
		Ans=(C((m-1)+2*n-j-1+2,3*n-j-1+2)-C(n+2*n-j-1,3*n-j-1+1)*(m-n)-C(n+2*n-j-1+1,3*n-j-1+2))%mod;
//		fo(j,0,n)
//		add(ans,1ll*(m-i)*C(n,j)%mod*C(i-n-1+(n*3-j),n*3-j-1)%mod*qpower(2,n-j)%mod*qpower(2*K-1,j));
		add(ans,Ans*C(n,j)%mod*qpower(2,n-j)%mod*qpower(2*K-1,j));
	}
	printf("%lld
",(ans+mod)%mod);
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}