loj#2249. 「NOI2014」购票

题目描述

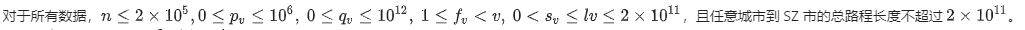
题解

不知道有没有一个log的，两个log简单自然

没有l限制的一个log做法：很显然的想法是dfs维护栈二分，问题是要弹栈

用树来维护栈，一个点到根的路径就是该点处的栈，倍增弹栈&查找即可一个log

加上l限制后会出问题，考虑naive的log^3做法，直接树剖线段树维护凸壳+二分

发现一个点的询问范围是若干重链前缀+一条重链中间一段，后者线段树维护前者dfs时维护，dfs时先走轻边后走重边即可，两部分都是log^2

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define inf 9223372036854775807ll
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define ll long long
//#define file
using namespace std;

int a[200001][2],ls[200001],fa[200001][18],size[200001],nx[200001],top[200001];
int bg[200001],ed[200001],d[200001],n,i,j,k,l,len,tot;
ll S[200001][18],p[200001],q[200001],L[200001],dp[200001],f[200001];

double js(int t1,int t2) {return 1.0*(f[t2]-f[t1])/(-dp[t1]+dp[t2]);}
struct type{
	vector<int> d;
	vector<double> D;
	int t;
	
	void clear() {t=0;d.clear();D.clear();}
	void add(int x)
	{
		int i;
		while (t>1 && js(x,d[t-1])<=D[t-2]) --t,d.pop_back(),D.pop_back();
		++t;
		d.push_back(x);if (t>1) D.push_back(js(d[t-2],d[t-1]));
	}
	ll find(int p)
	{
		if (!t) return inf;
		if (t==1) return -dp[d[0]]*p+f[d[0]];
		
		int l=1,r=t-1,mid;
		while (l<r)
		{
			mid=(l+r)/2;
			if (D[mid-1]<=p) l=mid+1; else r=mid;
		}
		l+=D[l-1]<=p;
		return -dp[d[l-1]]*p+f[d[l-1]];
	}
} P[21];
struct tree{
	int tr[1000001][2],len;
	type Tr[1000001];
	
	void New(int t,int x) {if (!tr[t][x]) tr[t][x]=++len;}
	void change(int t,int l,int r,int x,int s)
	{
		int mid=(l+r)/2;
		Tr[t].add(s);
		if (l==r) return;
		
		if (x<=mid) New(t,0),change(tr[t][0],l,mid,x,s);
		else New(t,1),change(tr[t][1],mid+1,r,x,s);
	}
	ll find(int t,int l,int r,int x,int y,int p)
	{
		int mid=(l+r)/2;
		ll ans=inf,s;
		if (x<=l && r<=y) return Tr[t].find(p);
		
		if (x<=mid) s=find(tr[t][0],l,mid,x,y,p),ans=min(ans,s);
		if (mid<y) s=find(tr[t][1],mid+1,r,x,y,p),ans=min(ans,s);
		return ans;
	}
} tr;

void New(int x,int y) {++len;a[len][0]=y;a[len][1]=ls[x];ls[x]=len;}
void dfs(int t)
{
	int i,mx=0;
	fo(i,1,17) fa[t][i]=fa[fa[t][i-1]][i-1],S[t][i]=S[t][i-1]+S[fa[t][i-1]][i-1];
	dp[t]=dp[fa[t][0]]+S[t][0],d[t]=d[fa[t][0]]+1;
	
	size[t]=1;
	for (i=ls[t]; i; i=a[i][1])
	{
		dfs(a[i][0]);
		if (size[a[i][0]]>mx) mx=size[a[i][0]],nx[t]=a[i][0];
		size[t]+=size[a[i][0]];
	}
}
void Dfs(int t)
{
	int i;
	
	bg[t]=++j,ed[top[t]]=max(ed[top[t]],j);
	if (nx[t]) top[nx[t]]=top[t],Dfs(nx[t]);
	
	for (i=ls[t]; i; i=a[i][1])
	if (a[i][0]!=nx[t])
	{
		top[a[i][0]]=a[i][0];
		Dfs(a[i][0]);
	}
}

int jump(int t,ll s)
{
	int i;
	if (s>=dp[t]) return 1;
	fd(i,17,0) if (s>=S[t][i]) s-=S[t][i],t=fa[t][i];
	return t;
}

void DFS(int t)
{
	int i,j,k,l;
	ll s;
	
	if (t>1)
	{
		f[t]=inf,j=jump(t,L[t]),l=t;
		fd(i,tot,1)
		if (d[top[l]]<=d[j])
		{
			s=(i==tot)?tr.find(top[l],bg[top[l]],ed[top[l]],bg[j],bg[fa[l][0]],p[t]):tr.find(top[l],bg[top[l]],ed[top[l]],bg[j],bg[l],p[t]);
			f[t]=min(f[t],s);break;
		}
		else
		{s=P[i].find(p[t]),f[t]=min(f[t],s);l=fa[top[l]][0];}
		f[t]=f[t]+dp[t]*p[t]+q[t];
	}
	
	tr.change(top[t],bg[top[t]],ed[top[t]],bg[t],t);
	P[tot].add(t);
	
	for (i=ls[t]; i; i=a[i][1])
	if (a[i][0]!=nx[t])
	{
		++tot;P[tot].clear();
		DFS(a[i][0]);
		--tot;
	}
	if (nx[t]) DFS(nx[t]);
}

int main()
{
	#ifdef file
	freopen("loj2249.in","r",stdin);
	freopen("loj2249.out","w",stdout);
	#endif
	
	scanf("%d%d",&n,&i);tr.len=n;
	fo(i,2,n) scanf("%d%lld%lld%lld%lld",&fa[i][0],&S[i][0],&p[i],&q[i],&L[i]),New(fa[i][0],i);
	
	dfs(1);
	j=0,top[1]=1,Dfs(1);
	tot=1;DFS(1);
	
	fo(i,2,n) printf("%lld
",f[i]);
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}