多项式小结（求逆、求导、积分、ln、牛顿迭代、exp）

目录

• 求逆
• 求导
• 复合函数求导
• 积分
• ln
• 牛顿迭代
• exp
  • 正确性证明
• n^2lnexp
  • exp
  • ln
• 快速幂
• 时间复杂度
• 调试方法&注意事项
• 例题
• 题解
• code

求逆

求(A(x)B(x)equiv 1(mod;x^n))，下文为了方便表述把n/2

已知(A(x)C(x)equiv 1(mod;x^n))，倍增求(A(x)B(x)equiv 1(mod;x^{2n}))，下文为了方便把(x)省掉

(A(B-C)equiv 0(mod;x^n))

(A^2(B-C)^2equiv 0(mod;x^{2n}))

(A(B-C)^2equiv 0(mod;x^{2n}))

(AB^2-2ABC+AC^2equiv 0(mod;x^{2n}))

(B-2C+AC^2equiv 0(mod;x^{2n}))

(Bequiv 2C-AC^2(mod;x^{2n}))

求导

求(A'(x))，本质是求一点的斜率，定义(A_i=A(x)[x^i])

(A'(x)=frac{sum A_i((x+Delta)^i-x^i}{Delta})

当(Delta ightarrow0)时(A'(x)=sum_{i>=1} iA_ix^{i-1})

复合函数求导

(G(x)=F(A(x)),G'(x)=F'(A(x))A'(x))

这个的意义是以x为自变量的导，而(F'(A(x)))的意义是以A(x)为自变量的导

所以ln中求的是G'(x)，牛顿迭代把A当作自变量求的是F'(A(x))

积分

是不定积分，即求导的逆运算

(int A(x)=sum_{i>=1} frac{1}{i}x^iB_{i-1})

积分后再求导常数项会消失

ln

求(G(x)=ln(F(x)))，具体的意义是什么并不是很知道

复合函数求导：(G(x)=F(A(x)))，(G'(x)=F'(A(x))A'(x))，并且有(ln'(x)=frac{1}{x})

(G'(x)=frac{F'(x)}{F(x)})

(G(x)=int frac{F'(x)}{F(x)})

牛顿迭代

对于普通的多项式(A(x))求零点x，设上一次求得的是x0（不一定是零点）

在((x0,f(x0)))处做切线，斜率为(f'(x0))，则根据简单三角函数有

(frac{f(x0)}{x0-x}=f'(x0))

(x=x0-frac{f(x0)}{f'(x0)})

牛顿迭代求的是近似解，但

exp

先不考虑精度，求(B(x)=e^{A(x)}(mod;x^n))

(ln(B(x))=A(x)(mod;x^n))

(ln(B(x))-A(x)=0(mod;x^n))

把B当作变量，A当作常数并不知道为什么可以这样

设(F(B(x))=ln(B(x))-A(x))，则(F'(B(x))=frac{1}{B(x)})（函数相加的导数=分别的导数和，A看作常数了所以是0）

把n/2，代牛顿迭代的式子，设(C(x))是模(x^n)下的解，求模(x^{2n})下的解(B(x))

(B(x)=C(x)-C(x)(ln(C(x))-A(x))(mod;x^{2n}))

(B(x)=C(x)(1-ln(C(x))+A(x))(mod;x^{2n}))

正确性证明

泰勒展开：

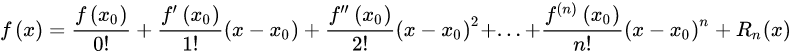
x即(B(x))，x0即(C(x))，相减之后前n项是0，平方之后前2n项是0，于是被模掉了（

所以只剩前两项了，根据牛顿迭代的定义

发现取的就是前两项，现在只剩前两项了，所以是精确解（

其实模完之后变成了一条直线，所以可以求解

n^2lnexp

模数不是ntt模数时可以用，也有学的必要

https://www.cnblogs.com/gmh77/p/13162153.html

exp

设(g(x)=e^{f(x)})，设(g_n)为(g(x)[x^n])，(f_n)为(f(x)[x^n])

(g(x)=e^{f(x)})

(g'(x)=e^{f(x)}f'(x))

因为(f'(x)=sum{i*x^{i-1}f_i})

所以(xf'(x)=sum_{i>=1}{i*x^if_i})

(ng_n=sum_{i=0}^{n}{g_{n-i}if_i})

硬点g0=1，然后即可n^2求得exp

原因是f(x)没有常数项（否则求不出来），所以(e^x)展开后只有(frac{x^0}{0!}=1)

ln

(ng_n=sum_{i=0}^{n-1}{g_{n-i}if_i}+nf_n)

(nf_n=ng_n-sum_{i=0}^{n-1}{g_{n-i}if_i})

快速幂

先ln，乘上系数后exp

lnexp来搞是线性卷积，dft再乘k是循环卷积

时间复杂度

上面的那一坨都是nlogn的，但是常数略大

调试方法&注意事项

一定要把不用的位置清空，相乘长度开到长度和

两个长度为N的多项式相乘时一定要把[N,2N-1]清空

调试小技♂巧：

快速幂->exp->ln->求导积分求逆->NTT，从后往前调试

要测小数据和中数据，多测几遍+改n和len看有没有变

ln再exp和exp再ln结果不变，可以利用这点来查错

可以在不用的位上加一些数看答案是否会改变

exp的组合意义：(e^x=sum frac{x^i}{i!})，所以可以手玩判断exp是否写对

如果exp对了而ln+exp/exp+ln错了那就是数组没有清空

例题

6712.【2020.06.09省选模拟】题3

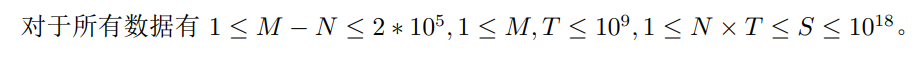
题解

推式子省略，变成快速幂

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define C(n,m) (jc[n]*Jc[m]%998244353*Jc[(n)-(m)]%998244353)
#define mod 998244353
#define Mod 998244351
#define G 3
#define ll long long
#define file
using namespace std;

ll A2[524288],a[524288],b[524288],c[524288],w[524288],S,T,n,m,s;
int a2[20][524288],i,j,k,l,N,len;

ll qpower(ll a,int b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}

//static ll a[maxn];
void dft(ll *a,int tp,int N,int len)
{
	int i,j,k,l,S=N,s1=2,s2=1;
	ll u,v,w,W;
	
	fo(i,0,N-1) A2[i]=a[a2[len][i]];
	memcpy(a,A2,N*8);
	
	fo(i,1,len)
	{
		W=(tp==1)?qpower(G,(mod-1)/s1):qpower(G,(mod-1)-(mod-1)/s1);S>>=1;
		fo(j,0,S-1)
		{
			w=1;
			fo(k,0,s2-1)
			{
				u=a[j*s1+k],v=a[j*s1+k+s2]*w;
				a[j*s1+k]=(u+v)%mod;
				a[j*s1+k+s2]=(u-v)%mod;
				w=w*W%mod;
			}
		}
		s1<<=1,s2<<=1;
	}
}
namespace Mul{ll a[524288],b[524288];}
void mul(ll *a,ll *b,ll *c,int N,int len)
{
	ll N2=qpower(N,Mod);
	int i,j,k,l;
	
	memcpy(Mul::a,a,N*8),memcpy(Mul::b,b,N*8);
	dft(Mul::a,1,N,len);dft(Mul::b,1,N,len);
	fo(i,0,N-1) c[i]=Mul::a[i]*Mul::b[i]%mod;
	dft(c,-1,N,len);
	fo(i,0,N-1) c[i]=c[i]*N2%mod;
}
namespace Ny{ll a[524288],b[524288];}
void ny(ll *a,ll *b,int N,int len)
{
	int i,j,k,l;
	
	memset(b,0,N*8);
	if (N==1) {b[0]=qpower(a[0],Mod); return;}
	ny(a,b,N/2,len-1);
	
	memset(Ny::a,0,N*16);
	mul(b,b,Ny::a,N,len);
	memset(Ny::b,0,N*16);
	fo(i,0,N-1) Ny::b[i]=a[i];
	mul(Ny::a,Ny::b,Ny::a,N*2,len+1);
	fo(i,0,N-1) b[i]=(b[i]*2-Ny::a[i])%mod;
}
void dao(ll *a,int N)
{
	int i;
	fo(i,0,N-2) a[i]=a[i+1]*(i+1)%mod;a[N-1]=0;
}
void ji(ll *a,int N)
{
	int i;
	fd(i,N-1,1) a[i]=a[i-1]*w[i]%mod;a[0]=0;
}
namespace LN{ll a[524288];}
void Ln(ll *a,int N,int len)
{
	int i;
	memset(LN::a,0,N*16);memcpy(LN::a,a,N*8);
	ny(LN::a,a,N,len);dao(LN::a,N);
	mul(a,LN::a,a,N*2,len+1);
	ji(a,N);fo(i,N,N+N-1) a[i]=0;
}
namespace EXP{ll a[524288];}
void Exp(ll *a,ll *b,int N,int len)
{
	int i,j,k,l;
	
	memset(b,0,N*8);
	if (N==1) {b[0]=1;return;}
	Exp(a,b,N/2,len-1);
	
	memset(EXP::a,0,N*8);memcpy(EXP::a,b,N*4);
	Ln(EXP::a,N,len);
	fo(i,0,N-1) EXP::a[i]=(-EXP::a[i]+a[i])%mod;++EXP::a[0];fo(i,N,N+N-1) EXP::a[i]=0;
	mul(b,EXP::a,b,N*2,len+1);fo(i,N,N+N-1) b[i]=0;
}
namespace Mi{ll a[524288];}
void mi(ll *a,ll k,int N,int len)
{
	ll s=qpower(a[0],k);
	int i;
	
	memcpy(Mi::a,a,N*8);
	Ln(Mi::a,N,len);
	fo(i,0,N-1) Mi::a[i]=Mi::a[i]*(k%mod)%mod;
	Exp(Mi::a,a,N,len);
	fo(i,0,N-1) a[i]=a[i]*s%mod;
}

void init()
{
	int I,s=1;
	w[1]=1;
	fo(i,2,200000) w[i]=mod-w[mod%i]*(mod/i)%mod;
	
	fo(I,0,19)
	{
		fo(i,0,s-1)
		{
			j=i;k=0;
			fo(l,1,I) k=k*2+(j&1),j>>=1;
			a2[I][i]=k;
		}
		s*=2;
	}
}
void work()
{
	s=1;fo(i,1,m-n+1) s=s*((T-i+1)%mod)%mod*w[i]%mod,a[i-1]=s;
	s=1;fo(i,0,m-n) b[i]=s,s=s*(((S-n*T)-(i+1)+1)%mod)%mod*w[i+1]%mod;
	mi(a,n,N,len);
	mul(a,b,a,N*2,len+1);
}

int main()
{
	freopen("sum.in","r",stdin);
	#ifdef file
	freopen("sum.out","w",stdout);
	#endif
	
	scanf("%lld%lld%lld%lld",&S,&T,&n,&m);len=ceil(log2(m-n+1));N=qpower(2,len);
	init();
	
	work();
	printf("%lld
",(a[m-n]+mod)%mod);
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}