6486. 【GDOI2020模拟02.25】向日葵人生

题目描述

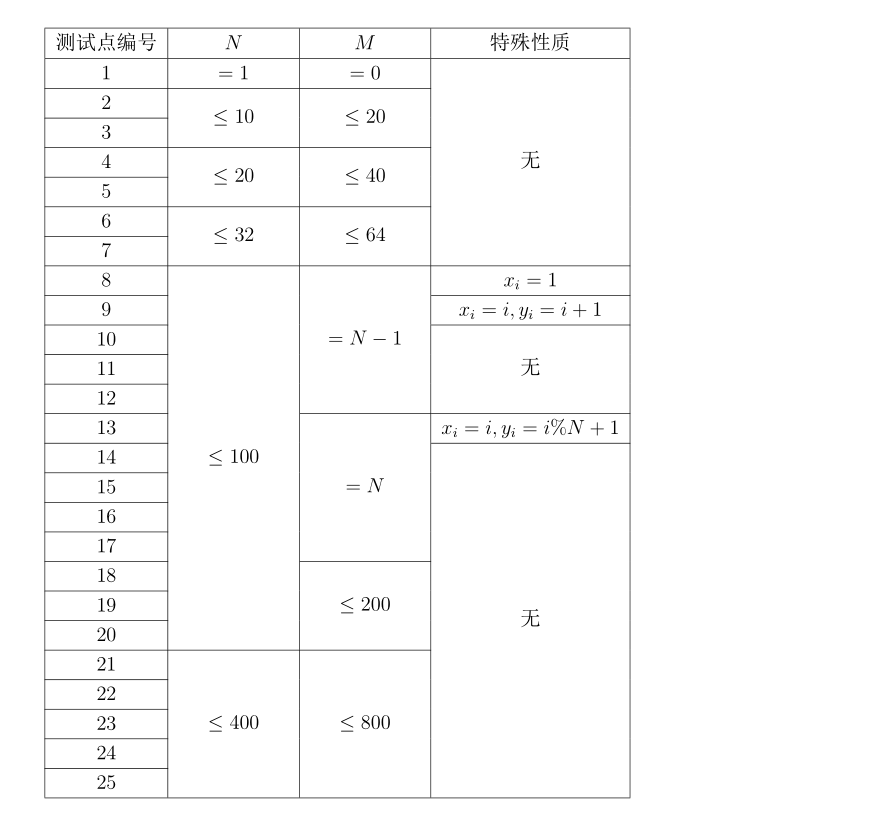
题解

显然可以求i删掉时j的贡献

不能把环单独割开，大概是计算的主体不相同？

考虑一条i到j的路径，如果i到j上没有环则期望为1/len

否则即∑f(x)*|x|，x表示一个使ij连通的集合

其实不需要算方案数，考虑直接算概率

概率又不好直接算，所以dp维护容斥系数

如果一个环被分成大小为ab的两部分，那么期望是1/a+1/b-1/(a+b-1)，-1是重复的点

在多个环的情况下容斥系数=(-1)^选择的整环个数

因为直接算概率，所以不需要考虑未满的那一边的具体选法，因此对于一个环最多只有三种转移

所以时间复杂度为O(n^3)

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define C(n,m) (jc[n]*Jc[m]%998244353*Jc[(n)-(m)]%998244353)
#define add(a,b) a=((a)+(b))%998244353
#define min(a,b) (a<b?a:b)
#define mod 998244353
#define Mod 998244351
#define ll long long
#define file
using namespace std;

int a[1602][2],ls[1602],num[1602],g[1602],dfn[1602],low[1602],Sum[1602],N,len,n,m,i,j,k,l,L,NUM,tot,son;
ll jc[401],Jc[401],w[401],d[1602],f[401][401],ans;
bool bz[1602],Bz[1602];

void New(int x,int y)
{
	++len;
	a[len][0]=y;
	a[len][1]=ls[x];
	ls[x]=len;
}

long long qpower(long long a,int b)
{
	long long ans=1;
	
	while (b)
	{
		if (b&1)
		ans=ans*a%mod;
		
		a=a*a%mod;
		b>>=1;
	}
	return ans;
}

void Dfs(int Fa,int t)
{
	int i;
	bz[t]=1;
	
	for (i=ls[t]; i; i=a[i][1])
	if (!bz[a[i][0]])
	{
		son+=(t==1);
		Dfs(t,a[i][0]);
	}
}

void dfs(int Fa,int t)
{
	int i;
	
	dfn[t]=low[t]=++j;
	bz[t]=1;
	
	for (i=ls[t]; i; i=a[i][1])
	if (!Bz[i])
	{
		Bz[i]=Bz[i^1]=1;
		
		if (!dfn[a[i][0]])
		{
			d[++tot]=i;
			
			dfs(t,a[i][0]);
			low[t]=min(low[t],low[a[i][0]]);
			
			if ((t>1 || son>1) && dfn[t]<=low[a[i][0]])
			{
				if (d[tot]==i)
				--tot;
				else
				{
					++N;
					num[d[tot]]=num[d[tot]^1]=N,g[N]=1,--tot;
					while (d[tot+1]!=i)
					num[d[tot]]=num[d[tot]^1]=N,++g[N],--tot;
				}
			}
		}
		else
		if (bz[a[i][0]] && dfn[a[i][0]]<dfn[t])
		low[t]=min(low[t],dfn[a[i][0]]),d[++tot]=i;
		
		Bz[i]=Bz[i^1]=0;
	}
	
	if (t==1 && tot>2)
	{
		++N;
		while (tot)
		num[d[tot]]=num[d[tot]^1]=N,++g[N],--tot;
	}
}

void dfs2(int Fa,int t,int Ls,int T,int sum)
{
	int i,j,k,l;
	bz[t]=1;
	
	if (Fa)
	{
		if (Ls)
		{
			fo(i,1,n)
			{
				if (i+sum<=n) add(f[t][i+sum],f[T][i]);
				if (i+(g[Ls]-sum)<=n) add(f[t][i+(g[Ls]-sum)],f[T][i]);
				if (i+(g[Ls]-1)<=n) add(f[t][i+(g[Ls]-1)],-f[T][i]);
			}
		}
		else
		{
			fo(i,1,n-1)
			add(f[t][i+1],f[T][i]);
		}
	}
	
	for (i=ls[t]; i; i=a[i][1])
	if (!bz[a[i][0]])
	{
		if (!num[i])
		dfs2(t,a[i][0],0,t,0);
		else
		if (Ls!=num[i])
		dfs2(t,a[i][0],num[i],t,1);
		else
		dfs2(t,a[i][0],Ls,T,sum+1);
	}
}

int main()
{
	freopen("falldream.in","r",stdin);
	#ifdef file
	freopen("falldream.out","w",stdout);
	#endif
	
	len=1;
	jc[0]=jc[1]=Jc[0]=Jc[1]=w[1]=1;
	fo(i,2,400)
	{
		w[i]=mod-w[mod%i]*(mod/i)%mod;
		
		jc[i]=jc[i-1]*i%mod;
		Jc[i]=Jc[i-1]*w[i]%mod;
	}
	
	scanf("%d",&NUM);
	scanf("%d%d",&n,&m);
	fo(i,1,m)
	scanf("%d%d",&j,&k),New(j,k),New(k,j);
	
//	---
	
	Dfs(0,1);
	memset(bz,0,sizeof(bz));j=0;
	dfs(0,1);
	
	fo(i,1,n)
	{
		memset(bz,0,sizeof(bz));
		memset(f,0,sizeof(f));
		f[i][1]=1;
		
		dfs2(0,i,-1,i,0);
		
		fo(j,1,n)
		{
			fo(k,1,n)
			add(ans,w[k]*f[j][k]);
		}
	}
	printf("%lld
",(ans+mod)%mod);
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}