题目描述
Description
Input
Output
Sample Input
INPUT1:
1 19
1
2
3
4
5
6
7
8
9
10
233
2333
23333
666
6666
66666
233666
2333666
2336666
INPUT2:
3 19
1
2
3
4
5
6
7
8
9
10
233
2333
23333
666
6666
66666
233666
2333666
2336666
INPUT3:
4 19
1
2
3
4
5
6
7
8
9
10
233
2333
23333
666
6666
66666
233666
2333666
2336666
Sample Output
OUTPUT1:
1
2
16
512
65536
33554432
838860732
32990492
932051910
764027380
910542875
838272742
930396622
739073573
9640642
263530905
865002813
765241490
139162994
OUTPUT2:
1
4
96
12288
7864320
201326568
293254325
515159244
840150399
651897566
739847860
531834902
591536684
577191249
16871820
69912188
532033966
249862507
753329879
OUTPUT3:
1
6
336
144384
406978560
696247661
369344513
934897514
881712217
545090322
736653783
184801125
483435346
490162119
818998946
456359890
676845946
879346635
854963600
Data Constraint
题解
看不懂题解
分解x后发现,x的质因子的次数最多为2
所以分解之后分别考虑次数为1和2的,方案=((为1的大小为n的方案)^{次数为1的个数}*(为2的大小为n的方案)^{次数为2的个数}*考虑负数的方案)
负数的方案为(2^{(n-1)*(n-1)}),因为前(n-1)*(n-1)可以任选,可以通过后面一行/列来调整(这里的方案是唯一的)
显然为1的方案为n!,这里重点求为2的方案
设f[n]表示n*n的合法方案数(即每行/列的和都为2)
考虑转移,在新加的一列中放数
①
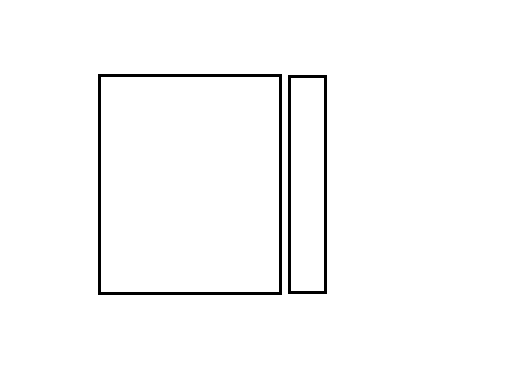
在最后一列放一个2
答案显然是f[n-1]*n
②
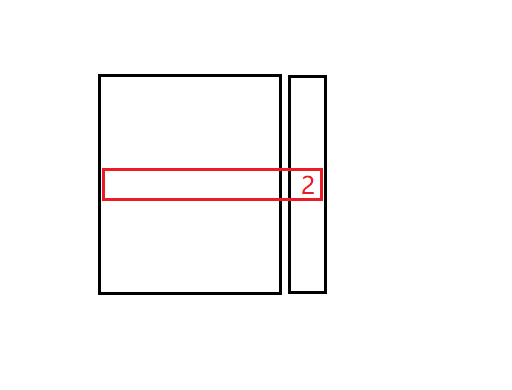
在最后一列放两个1
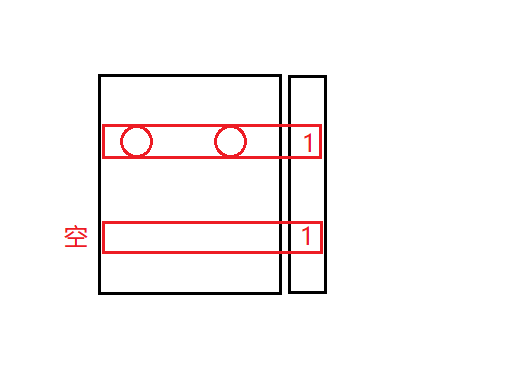
由于之前的(n-1)*(n-1)都放满了,所以两个1当中一定有某一个放在空行,另一个放在满行
这时钦定把满行的后一个给拉到空行,可以发现这样刚好可以唯一对应一种n*n的方案
答案是f[n-1]*n*(n-1)
③
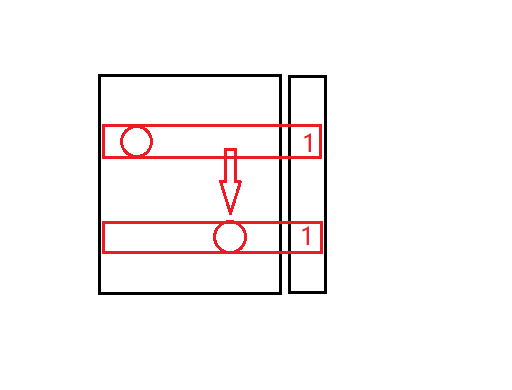
然而发现上面的还是会算重
可以发现,算重的是这样的情况:
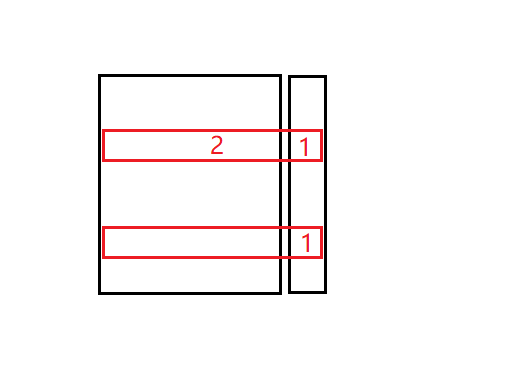
这样从上面拉下来和从下面拉上去是一样的
总数等价于
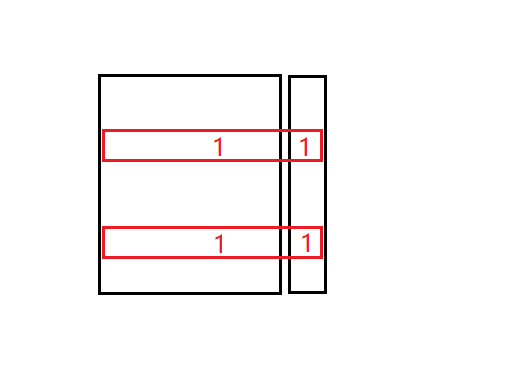
的方案
那么算重的方案为f[n-2]*C(n,2)*(n-1)
所以最终
f[n]=f[n-1]*n+f[n-1]*n*(n-1)-f[n-2]*C(n,2)*(n-1)
code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define two 499122177
#define mod 998244353
#define N 5000000
using namespace std;
long long F[N+1];
long long f[N+1];
long long x,s1,s2,I;
int T,n,i,j,k,l;
long long qpower(long long a,long long b)
{
long long ans=1;
while (b)
{
if (b&1)
ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
void init()
{
I=2;
while (x>1 && I<=100000)
{
if (!(x%I))
{
i=0;
while (!(x%I))
{
++i;
x/=I;
}
if (i==1)
++s1;
else
++s2;
}
++I;
}
if (x>1)
++s1;
}
void Init()
{
F[0]=1;f[0]=1;
F[1]=1;f[1]=1;
fo(i,2,N)
{
F[i]=F[i-1]*i%mod;
f[i]=(f[i-1]*i%mod*i%mod-f[i-2]*i%mod*(i-1)%mod*two%mod*(i-1)%mod)%mod;
if (f[i]<0)
f[i]+=mod;
}
}
int main()
{
freopen("pj.in","r",stdin);
freopen("pj.out","w",stdout);
scanf("%lld%d",&x,&T);
init();
Init();
for (;T;--T)
{
scanf("%d",&n);
printf("%lld
",qpower(F[n],s1)*qpower(f[n],s2)%mod*qpower(2,(long long)(n-1)*(n-1))%mod);
}
}