20172301 《程序设计与数据结构》第五周学习总结
教材学习内容总结
- 静态方法(类方法):不用实例化该类。
- 泛型方法:
- 不是创建一个引用泛型参数的类,而是创建一个引用泛型的方法。泛型参数只应用于该方法。
- 泛型声明必须位于返回类型之前,这样泛型才是返回类型的一部分。
例:
public static <T extends Comparable<T>> boolean LinearSearch (T[] data, int min, int max, T target)
查找
- 定义:查找在一个查找池中寻找目标元素或者找不到目标元素,返回button值true或flase。(注意:编写代码时要考虑全面,注意找不到目标元素时操作。)
- 线性查找法
- 原理:从列表头开始比较每一个值,直到找到该目标元素或者到达列表尾部目标元素不存在。从一段开始进行线性查找。
- 优缺点:对数组要求不高,易理解;效率不高,适用数组长度低。
- 时间复杂度O(n)。是线性的,直接与待查找元素数目成比例。
- 二分查找法
- 原理:取数组索引的中间和目标元素进行比较大小,然后再取另一半的中间和目标元素进行比较。直到找到该目标元素或者到达列表尾部目标元素不存在。
- 优缺点:效率高;数组需要排序,适用于大型项目组。
- 时间复杂度O(log2n)。
排序
-
定义:排序在基于某一个标准,将一些元素按照一定顺序排列。
-
基于效率排序:顺序排序(使用一对嵌套循环对n个元素进行排序,需要大约n^2次比较),对数排序(对n个元素进行排序需要大约nlog2n次比较)。
-
顺序排序:选择排序,插入排序,冒泡排序。
-
对数排序:快速排序,归并排序。
-
选择排序:
- 原理:每次都遍历数组, 从中选择出最大 (最小) 的元素,放在数组的第一位, 直到所有元素全部排序完成。
- 优缺点:应该是最好理解的,最为简单直观的排序方法;选择排序在不同的场景下都会执行相同次数的遍历,所以性能不是很高。
- 时间复杂度是O (n^2) 。
-
插入排序:
- 原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
- 优缺点:插入排序较适应于元素少的数组进行排序。
- 时间复杂度:如果数组本来就是有序的, 那么此时的复杂度为O (n) ;如果数组本来是倒序的,那么插入排序的时间复杂度就为O (n^2)。
- 有个形象的图来分析插入排序,斗地主大部分人都玩过吧:

-
冒泡排序:
- 原理是将前后每两个数进行比较,较大的数往后排,一轮下来最大的数就排到最后去了。然后再进行第二轮比较,第二大的数也排到倒数第二了,以此类推。
- 它的最佳时间复杂度是O(n^2)。
-
快速排序:
- 原理:属于交换类排序,是采用不断的比较和移动来实现排序的。增大了记录的比较和移动的距离,将关键字较大的记录从前面直接移动到后面,关键字较小的记录从后面直接移动到前面,从而减少了总的比较次数和移动次数。 同时采用“分而治之”的思想,把大的拆分为小的,小的拆分为更小的,其原理如下:对于给定的一组记录,选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分,直到序列中的所有记录均有序为止。
- 优缺点:一种非常高效的排序算法。
- 最坏时间复杂度
最坏情况是指每次区间划分的结果都是基准关键字的左边(或右边)序列为空,而另一边区间中的记录仅比排序前少了一项,即选择的关键字是待排序记录的最小值或最大值。最坏情况下快速排序的时间复杂度为O(n^2)。 - 最好时间复杂度
最好情况是指每次区间划分的结果都是基准关键字的左右两边长度相等或者相差为1,即选择的基准关键字为待排序的记录的中间值。此时进行比较次数总共为 nlogn,所以最好情况下快速排序的时间复杂度为O(nlogn)。 - 平均时间复杂度
快速排序的平均时间复杂度为O(nlogn)。在所有平均时间复杂度为O(nlogn)的算法中,快速排序的平均性能是最好的。
-
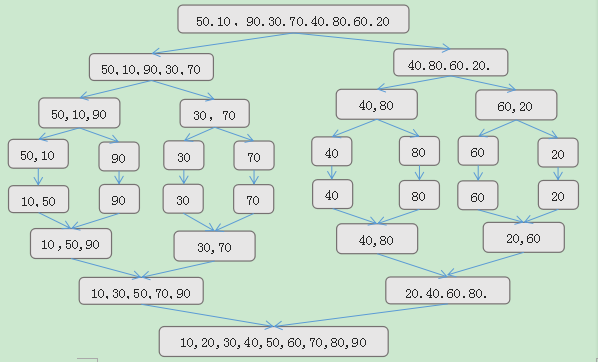
归并排序:
- 原理:对于给定的一组记录,利用递归与分治技术将数据序列划分成为越来越小的半子表,在对半子表排序,最后再用递归方法将排好序的半子表合并成为越来越大的有序序列。
- 优缺点:归并排序是一种比较占内存,但却效率高且稳定的算法。
- 整个归并排序需要进行log2n次,因此总的时间复杂度为O(nlogn),而且这是归并排序算法中最好、最坏、平均的时间性能。
-
基数排序:
- 原理:基于队列处理。 基于排序关键字的结构。例如在个位,十位,百位,分别遍历目标列表,然后通过队列的特征来排序。
- 时间复杂度为O(n)。
教材学习中的问题和解决过程
-
问题1:线性查找实现代码性能优化。(课上内容总结)
-
问题1解决方案:
- 原代码:
public static <T> boolean linearSearch(T[] data, int min, int max, T target) { int index = min; boolean found = false; while (!found && index <= max) { found = data[index].equals(target); index++; } return found; }- 课上我的想法是直接把equals方法放入到while循环条件当中,但是他对于查找的效率和性能并没有提升。
- 老师给出的答案是:设立一个哨兵,即为数组索引0处空出,使其等于目标元素,然后从数组尾部开始遍历,如果index == 0时,那么数组里面就没有这个元素。
data[0] = target; for (index = data.length-1; !data[indax].equals(target);--index){ } return index == 0? false:true;- 这个算法并没有从复杂度上对线性查找操作进行优化,但是在性能上有提高。不需要每一个循环像原先那样判断是否到了尾部。 可以看到,for循环里面没有任何操作,最后可以直接返回。
-
问题2:书P161 最下面有一行代码
public static <T extends Comparable<? super T>>
这个问号是什么鬼?又是书本的印刷问题?最后我在网上找到了相关资料。
- 问题2解决方案:
简单来说,这应该是java的泛型写法。
- 首先解释两个概念:Java中的通配符和边界
- 通配符:“?”就是一个占位符,它不表示任何具体的类型,而是表示符合定义规则的一个或者多个类型的一个占位标志。
- 边界:<? extends T> 表示上界通配符 它表示T以及T的子类, 类型最高是T;<? super T> 表示下界通配符 它表示T以及T的超类,类型最高可到Object ,最低是T。
为什么要用通配符和边界?
使用泛型的过程中,经常出现一种很别扭的情况。我们有Fruit类,和它的派生类Apple类。
class Fruit {}
class Apple extends Fruit {}
然后有一个最简单的容器:Plate类。盘子里可以放一个泛型的“东西”。我们可以对这个东西做最简单的“放”和“取”的动作:set( )和get( )方法。
class Plate<T>{
private T item;
public Plate(T t){item = t;}
public void set(T t){item = t;}
public T get(){ return item;}
}
现在我定义一个“水果盘子”,逻辑上水果盘子当然可以装苹果。
Plate<Fruit> p = Plate<Apple>(new Apple());
但实际上Java编译器不允许这个操作。会报错,“装苹果的盘子”无法转换成“装水果的盘子”。
error: incompatible types: Plate<Apple> cannot be converted to Plate<Fruit>
实际上,编译器脑袋里认定的逻辑是这样的:
苹果 IS-A 水果
装苹果的盘子 NOT-IS-A 装水果的盘子
所以,就算容器里装的东西之间有继承关系,但容器之间是没有继承关系的。所以我们不可以把Plate
什么是上界?
Plate <? extends Fruit>
翻译成人话就是:一个能放水果以及一切是水果派生类的盘子。再直白点就是:啥水果都能放的盘子。这和我们人类的逻辑就比较接近了。Plate<? extends Fruit>和Plate
Plate<? extends Fruit> p=new Plate<Apple>(new Apple());
如果把Fruit和Apple的例子再扩展一下,食物分成水果和肉类,水果有苹果和香蕉,肉类有猪肉和牛肉,苹果还有两种青苹果和红苹果。
//Lev 1
class Food{}
//Lev 2
class Fruit extends Food{}
class Meat extends Food{}
//Lev 3
class Apple extends Fruit{}
class Banana extends Fruit{}
class Pork extends Meat{}
class Beef extends Meat{}
//Lev 4
class RedApple extends Apple{}
class GreenApple extends Apple{}
什么是下界?
Plate<? super Fruit>
表达的就是相反的概念:一个能放水果以及一切是水果基类的盘子。Plate<? super Fruit>是Plate
上下界通配符的副作用
边界让Java不同泛型之间的转换更容易了。这样的转换也有一定的副作用。那就是容器的部分功能可能失效。
还是以刚才的Plate为例。我们可以对盘子做两件事,往盘子里set( )新东西,以及从盘子里get( )东西。
class Plate<T>{
private T item;
public Plate(T t){item = t;}
public void set(T t){item = t;}
public T get(){ return item;}
}
会使往盘子里放东西的set()方法失效。但取东西get()方法还有效。比如下面例子里两个set()方法,插入Apple和Fruit都报错。 ``` Plate p =new Plate上界<? extends T>不能往里存,只能往外取
public <T> List<T> fill(T...t);
但通配符没有这种约束,Plate单纯的就表示:盘子里放了一个东西,是什么我不知道。
下界<? super T>不影响往里存,但往外取只能放在Object对象里
使用下界<? super Fruit>会使从盘子里取东西的get( )方法部分失效,只能存放到Object对象里set( )方法正常。
Plate<? super Fruit> p = new Plate<Fruit>(new Fruit());
//存入元素正常
p.set(new Fruit());
p.set(new Apple());
//读取出来的东西只能存放在Object类里。
Apple newFruit3 = p.get(); //Error
Fruit newFruit1 = p.get(); //Error
Object newFruit2 = p.get();
因为下界规定了元素的最小粒度的下限,实际上是放松了容器元素的类型控制。既然元素是Fruit的基类,那往里存粒度比Fruit小的都可以。但往外读取元素就费劲了,只有所有类的基类Object对象才能装下。但这样的话,元素的类型信息就全部丢失。
PECS原则
频繁往外读取内容的,适合用上界Extends。
经常往里插入的,适合用下界Super。
- 问题3:书代码P177
@SuppressWarnings("unchecked")
是什么意思和用途?
- 问题3解决方案:
-
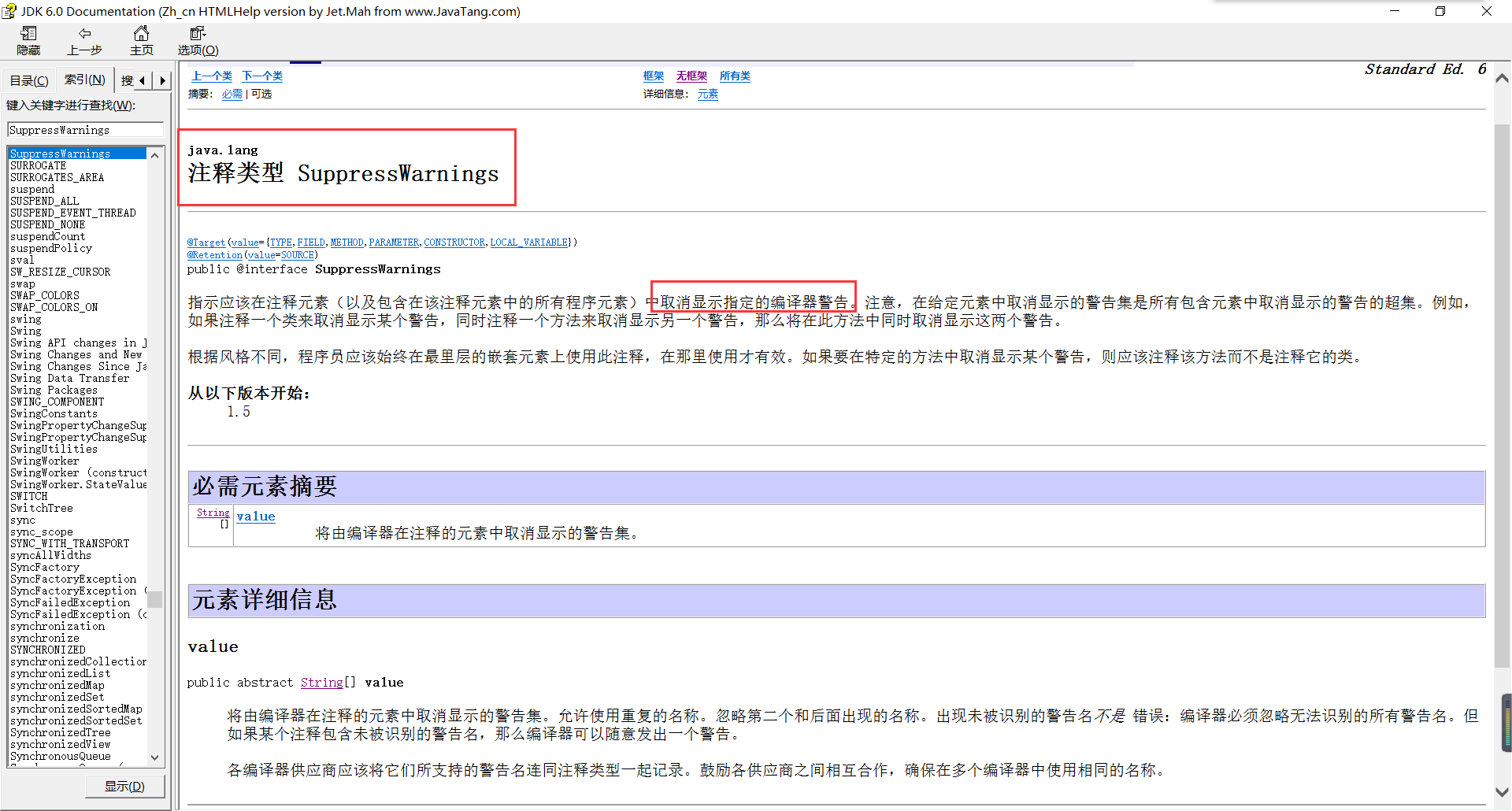
在API中竟然能查询到结果。它显示的是一种注释类型。
-
-
该批注的作用是给编译器一条指令,告诉它对被批注的代码元素内部的某些警告保持静默。 很多还不理解,先不咬文嚼字了。
-
代码调试中的问题和解决过程
这周代码比较简单。问题较小。
-
问题1:书上冒泡操作代码,在返回类型前声明了
<T extends Comparable<? super T>>,但是我在调用冒泡操作的swap方法时,却报错了错误。而且理由很不讲道理

-
问题1解决方案:
- 询问了学长学姐,发现了是swap方法的问题。swap方法并没有声明
Comparable<? super T>。 - 一方面,这体现了书上代码的不全面,顾头不顾尾;另一方面,也体现了自己思考问题不够全面,只片面的考虑了在本方法中的错误原因。
- 询问了学长学姐,发现了是swap方法的问题。swap方法并没有声明
-
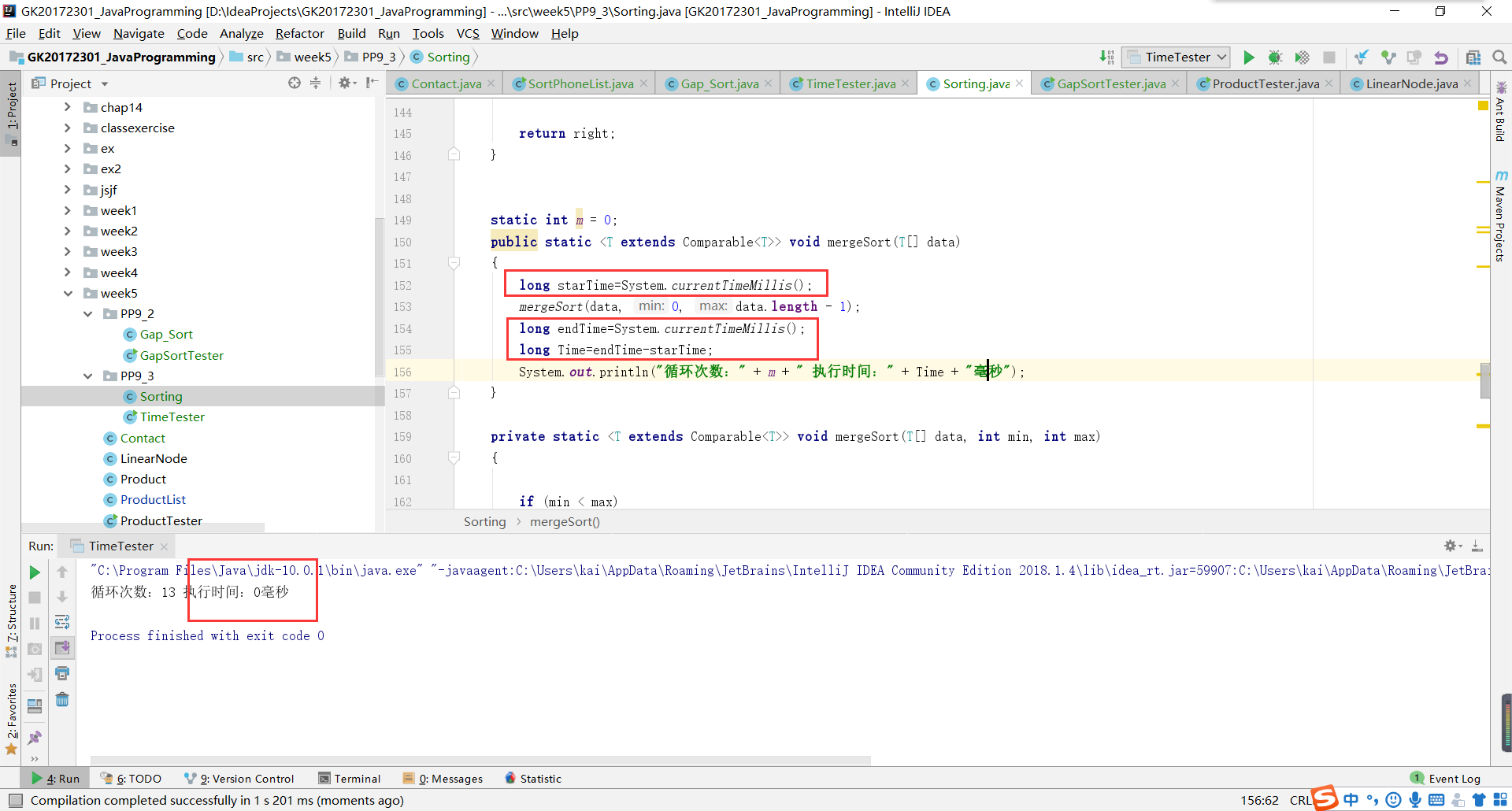
问题2:PP9.3的时间计算问题。在开始的时候,我用的计时单位是毫秒,在输出结果的时候,往往是0。这让我以为我的开始时间并没有计算,或者是什么。
-
问题2解决方案:
- 其实这就是一个精确度的问题。可能是运行的时间过快,也就0.0001毫秒的时间,计算机的精确度不够。
- 这时候我们需要更低一级的单位,纳秒。我的运行结果在几万纳秒左右。而1毫秒(ms) = 1000000纳秒(ns)。所以,我程序运行的实际结果大约在0.01毫秒左右。
代码托管

上周考试错题总结
上周考试无错题,优秀。
结对及互评
点评过的同学博客和代码
- 上周博客互评情况
其他
使时间充实就是幸福。 呼,没有什么想说的,只想歇一口气。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 10/10 | |
| 第二周 | 610/610 | 1/2 | 20/30 | |
| 第三周 | 593/1230 | 1/3 | 18/48 | |
| 第四周 | 2011/3241 | 2/5 | 30/78 | |
| 第五周 | 956/4197 | 1/6 | 22/100 |