第二节课
- 排序(快排、堆排、桶排、计数与基数排序简单介绍)
- 荷兰国旗问题
- 大根堆小根堆
- 排序稳定性
- 比较器
- 相邻两数的最大差值问题
1. 题目一:
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。
要求:时间复杂度O(N)、额外空间复杂度O(1)
该问题同荷兰国旗问题,见下:
2. 题目二:
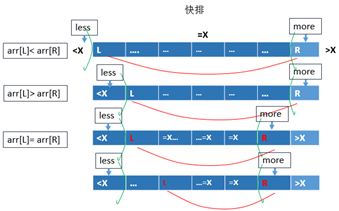
荷兰国旗问题:
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。
要求时间复杂度为O(N)、额外空间复杂度为O(1)。
分析:三个指针法:一个指向前头less,一个指向尾部more,一个是当前下标cur。当前下标由指向前面的指针推着前进。

代码如下:
public static int[] partition(int[] arr, int L, int R, int num) { int less = L-1; //小于 int more = R+1; //大于 int cur = L; //等于 while (cur<more) { if (arr[cur]<num) { swap(arr,++less,cur++); }else if (arr[cur]>num) { swap(arr,--more,cur); }else { cur++; } } return arr; } private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }
3. 快排
根据荷兰国旗问题,变形,让num=arr[arr.length-1],相当于R= arr.length-2;
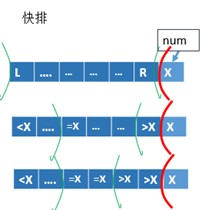
经典快排缺点:如[1,2,3,4,5,6,7…N],快排就成了O(N2);
改进:随机快排:即是选择num = arr[]中随机的元素。时间复杂度O(N*logN);额外空间复杂度O(logN);【最常用的】
非随机代码如下:
public static void quickSort(int[] arr, int L, int R) { if (L<R) { int[] p = partition(arr, L, R); quickSort(arr, L, p[0]-1); quickSort(arr, p[1], R); } } public static int[] partition(int[] arr, int L, int R) { int less = L-1; int more = R; int cur = L; while (cur<more) { if (arr[cur]<arr[R]) { swap(arr,++less,cur++); }else if (arr[cur]>arr[R]) { swap(arr,--more,cur); }else { cur++; } } swap(arr, more, R); return new int[] {less+1, more}; } private static void swap(int[] arr, int i, int j) { // TODO Auto-generated method stub int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }
随机快排代码如下:
public static void quickSort(int[] arr) { if (arr == null || arr.length < 2) { return; } quickSort(arr, 0, arr.length - 1); } public static void quickSort(int[] arr, int l, int r) { if (l < r) { swap(arr, l + (int) (Math.random() * (r - l + 1)), r); //随机选择一个数作为比较对象 int[] p = partition(arr, l, r); quickSort(arr, l, p[0] - 1); quickSort(arr, p[1] + 1, r); } } public static int[] partition(int[] arr, int l, int r) { int less = l - 1; int more = r; while (l < more) { if (arr[l] < arr[r]) { swap(arr, ++less, l++); } else if (arr[l] > arr[r]) { swap(arr, --more, l); } else { l++; } } swap(arr, more, r); return new int[] { less + 1, more }; } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; }
4. 堆排序
时间复杂度O(N*logN),额外空间复杂度O(1)
【堆结构非常重要】
- 堆结构的heapInsert和heapify;
- 堆结构的增大和减少;
- 如果只是建立堆的过程,时间复杂度为O(N);
- 优先级队列结构就是堆结构。
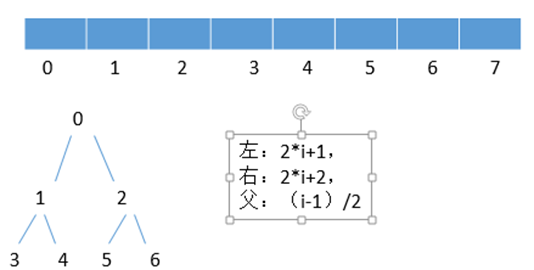
堆: 完全二叉树。每一层从左到右依次补齐,满二叉树属于完全二叉树。
当一个数组满足左:2*i+1,右:2*i+2,父:(i-1)/2就是完全二叉树结构。
大根堆:任何子树的最大值都是子树的根节点,
小根堆:任何子树的最小值都是子树的根节点。
用处:比如实时求所输入数据的中位数。
大根堆的建立:
有任何一个子树变成大根堆。复杂度=log1+ log2+… +logN=O(N)
public class HeapSort { public static void heapSort(int[] arr) { if (arr.length<2 || arr==null) { return; } for (int i = 0; i < arr.length; i++) { heapInsert(arr,i);//建立大根堆; } int heapSize = arr.length; swap(arr, 0, --heapSize); while (heapSize>0) { heapify(arr,0,heapSize);//调整大根堆 swap(arr, 0, --heapSize);//将大根堆的根和最后一个元素交换,然后size缩小一个; } } private static void heapify(int[] arr, int index, int size) { //找到left int left = 2*index+1; //进行循环 while (left<size) { //确定left和right中较大的位置 int largest = left+1<size && arr[left+1]<arr[left] ? left : left+1; //确定孩子和父节点中较大的位置 largest = largest>arr[index] ? largest : index; //如果最大位置和父节点位置相同,则跳出循环 if (largest == index) { break; } //否则,交换最大值和父节点的值,将变量更新 swap(arr, index, largest); index = largest; left = 2*index+1; } } private static void heapInsert(int[] arr, int index) {//如果插入节点值要比父节点值大,则交换,并且比较下一轮。 while (arr[index]>arr[(index-1)/2]) { swap(arr,index,(index-1)/2); index = (index-1)/2; } } private static void swap(int[] arr, int index, int i) { int temp = arr[i]; arr[i] = arr[index]; arr[index] = temp; } public static void main(String[] args) { // TODO Auto-generated method stub } }
5. 题目三
从一个流中不断生成数,求吐出的数的中位数。
同牛客网剑指OfferDay63

6. 排序的稳定性:
稳定性:排序外,相同元素保持出现的先后顺序。
复杂度是O(N2)
- l 冒泡排序:当遇到相同数时,该数不交换,将后面的数往下沉。可以稳定;
- l 插入排序:当遇到相同数时,该数不交换;可以稳定;
- l 选择排序:做不到稳定性。因为你要从后面的所有数中找到最小的,然后将前面的某一个a与该最值交换,如果有多个a存在,那么,a的先后顺序将无法保证。故做不到。
复杂度是O(N*logN)
- l 归并排序:merge时,当相同时先拷贝左边(小区域)的数;可以稳定
- l 快排:做不到稳定性;
- l 堆排:做不到稳定性。在建大根堆的时候,就都已经不能保证稳定性了。
工程中的排序:
- l 基础类型:快排
- l 自定义类型:归并排序(稳定性)
- l 如果数组长度较短:不管什么类型,都用插排(时间复杂度O(N^2)劣势显示不出来,反而额外空间复杂度O(1)较快)。
7. 比较器:
- 负数,第一个参数放前面(o1)
- 正数,第二个参数放前面(o2)
- 0,一样大
在笔试时候,如果不是考察排序,就直接调用系统的Arrays.sort(arr)即可。或者加上自定义的比较器Arrays.sort(arr,new myComparator());
- l 堆中的比较器
优先级队列实质上就是堆 ,分为大根堆,小根堆。
必须指定排序依据。

![]()
- TreeMap<T>红黑树结构
以下为非比较的排序(基于桶)
- 非基于比较的排序,与被排序的样本的实际数据状况很有关系,所以实际中并不经常使用;
- 时间复杂度O(N),额外空间复杂度O(N);
- 稳定的排序。
8. 桶排序:
词频,桶就是容器,可以是队列,可以是堆等,一个萝卜一个坑,按照数据状况分到每个桶。
题目四
给定一个数组,求如果排序之后,相邻两数的最大差值,要求时间复杂度O(N),且要求不能用非基于比较的排序。
思路:借用桶的概念,但没有进行桶排序。
先找到最大最小值,若max == min ,则数组中数据全相同,差值最大为0;
若max != min ,N个数,设定N+1个桶,每个桶范围是(max-min)/(N+1)
利用鸽笼问题,总有一个桶是空的,可以排除同一桶内的两个数的差值不是最大的。
记录每个桶内的最大,最小,以及是否进来过数。
给定某值i,以及数组最大最小值max,min和数组长度len,确定该值所在的桶的标号
bid = (int)(i-min)*len/(max-min),
public static int maxGap(int[] nums) { if (nums == null || nums.length < 2) { return 0; } int len = nums.length; int min = Integer.MAX_VALUE; int max = Integer.MIN_VALUE; for (int i = 0; i < len; i++) { min = Math.min(min, nums[i]); max = Math.max(max, nums[i]); } if (min == max) { return 0; } boolean[] hasNum = new boolean[len + 1]; int[] maxs = new int[len + 1]; int[] mins = new int[len + 1]; int bid = 0; for (int i = 0; i < len; i++) { bid = bucket(nums[i], len, min, max); mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i]; maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i]; hasNum[bid] = true; } int res = 0; int lastMax = maxs[0]; int i = 1; for (; i <= len; i++) { if (hasNum[i]) { res = Math.max(res, mins[i] - lastMax); lastMax = maxs[i]; } } return res; } public static int bucket(long num, long len, long min, long max) { return (int) ((num - min) * len / (max - min)); }
另附:
1. Java数据结构和算法(九)——高级排序,里面有快排的详细步骤,很好的一篇文章!