第一节课
- 复杂度
- 排序(冒泡、选择、插入、归并)
- 小和问题和逆序对问题
- 对数器
- 递归
1. 复杂度
认识时间复杂度常数时间的操作:一个操作如果和数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的指标。常用O(读作big O)来表示。
具体来说,在常数操作数量的表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果记为f(N),那么时间复杂度为O(f(N))。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是常数项时间。
举例说明:
一个有序数组A,另一个无序数组B,请打印B中的所有不在A中的数,A数组长度为N,B数组长度为M。
算法流程1:对于数组B中的每一个数,都在A中通过遍历的方式找一下;
算法流程2:对于数组B中的每一个数,都在A中通过二分的方式找一下;
算法流程3:先把数组B排序,然后用类似外排的方式打印所有在A中出现的数;
三个流程,三种时间复杂度的表达...
如何分析好坏?
算法1:O(M*N);
算法2:二分:O(M*log2N);因为每次都砍一半,即砍了log2N次;简写logN,默认底数为2;
算法3:双指针法,
1). B排序:O(M*logM);
2). O(N+M);描述常数操作次数的估计;
总:O(M*logM)+ O(N+M)
若M较大,N较小≈O(M*logM)
若M较小,N较大≈O(N+M)
2. 排序
1. 冒泡排序:O(N2),额外空间复杂度为O(1);
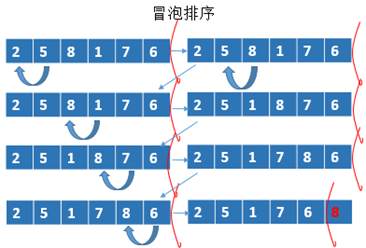
代码如下:
public static void bubbleSort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int e = arr.length - 1; e > 0; e--) { for (int i = 0; i < e; i++) { if (arr[i] > arr[i + 1]) { swap(arr, i, i + 1); } } } } public static void swap(int[] arr, int i, int j) { arr[i] = arr[i] ^ arr[j]; arr[j] = arr[i] ^ arr[j]; arr[i] = arr[i] ^ arr[j]; }
2. 选择排序:O(N2),额外空间复杂度为O(1);【已不用】
从剩下的的数中选择出最小/大的加入。
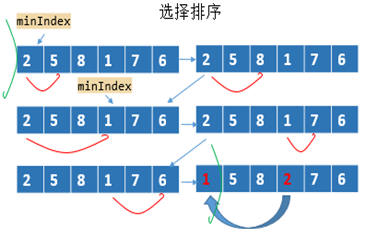
代码如下:
public static void selectionSort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = 0; i < arr.length - 1; i++) { int minIndex = i; for (int j = i + 1; j < arr.length; j++) { minIndex = arr[j] < arr[minIndex] ? j : minIndex; } swap(arr, i, minIndex); } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; }
3. 插入排序(扑克牌整牌):O(N2),额外空间复杂度为O(1);【经常用】
从剩下的数中选出下一个数,进行与前一位的数进行比较,然后再与前面的数比较,直到大于前一个数。
该复杂度与数据状况有关系:即实际的时间与数组的排列状况有关系,最好的情况是O(N),最差的情况是O(N2);

代码如下:
public static void insertionSort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = 1; i < arr.length; i++) { for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) { swap(arr, j, j + 1); } } } public static void swap(int[] arr, int i, int j) { arr[i] = arr[i] ^ arr[j]; arr[j] = arr[i] ^ arr[j]; arr[i] = arr[i] ^ arr[j]; }
4. 归并排序:O(N*logN),额外空间复杂度为O(N);
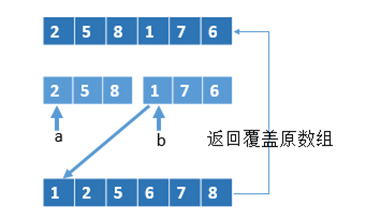
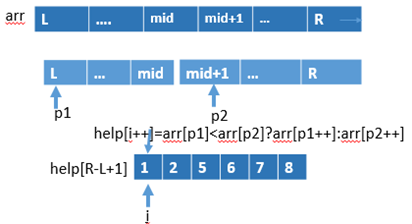
代码如下:
public static void mergeSort(int[] arr) { if (arr == null || arr.length < 2) { return; } mergeSort(arr, 0, arr.length - 1); } public static void mergeSort(int[] arr, int L, int R) { if (L == R) { return; } int mid = L + ((R - L) >> 1); //L和R中点的位置(L+R)/2 mergeSort(arr, L, mid); //T(n/2) mergeSort(arr, mid + 1, R); //T(n/2) merge(arr, L, mid, R); //O(N)
//T(N) = 2T(N/2) + O(N) } public static void merge(int[] arr, int L, int M, int R) { int[] help = new int[R - L + 1]; int i = 0; int p1 = L; int p2 = M + 1; while (p1 <= m && p2 <= r) { help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; }
//上述两个条件,必须有且只有一个越界,故要讨论两种情况,将剩下的跟到尾部 while (p1 <= M) { help[i++] = arr[p1++]; } while (p2 <= R) { help[i++] = arr[p2++]; } for (i = 0; i < help.length; i++) { arr[L + i] = help[i]; } }
3. 小和问题和逆序对问题:
1. 小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和。
例子:
[1,3,4,2,5]
1左边比1小的数,没有;
3左边比3小的数,1;
4左边比4小的数,1、3;
2左边比2小的数,1;
5左边比5小的数,1、3、4、2;
所以小和为1+1+3+1+1+3+4+2=16
分析:
小和问题,由当前数左侧所有比自己小的数之和相加 ==》转换为 ==》当前数右侧有多少个比自己大的,那么该数就乘以几,再相加之和;
该问题与归并排序类似:
代码如下:
public static int smallSum(int[] arr) { if (arr == null || arr.length < 2) { return 0; } return mergeSort(arr, 0, arr.length - 1); } public static int mergeSort(int[] arr, int L, int R) { if (L == R) { return 0; } int mid = L + ((R - L) >> 1); return mergeSort(arr, L, mid) + mergeSort(arr, mid + 1, R) + merge(arr, L, mid, R); } public static int merge(int[] arr, int L, int M, int R) { int[] help = new int[r - L + 1]; int i = 0; int p1 = L; int p2 = m + 1; int res = 0;//多加一个变量 while (p1 <= M && p2 <= R) { res += arr[p1] < arr[p2] ? (R - p2 + 1) * arr[p1] : 0; //多了这一句 help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; } while (p1 <= M) { help[i++] = arr[p1++]; } while (p2 <= R) { help[i++] = arr[p2++]; } for (i = 0; i < help.length; i++) { arr[L + i] = help[i]; } return res; }
2. 逆序对问题
在一个数组中,左边的数如果比右边的数大,则这两个数构成一个逆序对,请打印所有逆序对。
4. 对数器
对数器的概念和使用
步骤:
0,有一个你想要测的方法a,
1,实现一个绝对正确但是复杂度不好的方法b,
2,实现一个随机样本产生器
3,实现比对的方法
4,把方法a和方法b比对很多次来验证方法a是否正确。
5,如果有一个样本使得比对出错,打印样本分析是哪个方法出错
6,当样本数量很多时比对测试依然正确,可以确定方法a已经正确。
5. 递归
递归就是系统栈;把当前所有变量入栈计算完后返回现场。
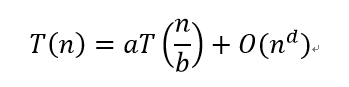
Master公式:
a是发生的次数


Over...