GIS从出现到为人所知,只不过经历了短短的几十年时间,尤其是近几年,大有欣欣向荣之势,越来越多的人开始了解GIS。自己和GIS打交道也快10年时间了,所从事的工作也是把“阳春白雪”变成“下里巴人”,让更多的人能理解并使用GIS,但每每向其他行业的人介绍GIS,还真不是三言两语可以讲清楚的事情,于是近日写得小文一篇,希望能够给想了解GIS的人一点点启发,也许GIS可以在你的工作中大显身手呢。
1. GIS:你能帮我做什么
“GIS是什么,能干什么?”,我想这个问题可能是困惑大多数GIS专业学生的问题,现在当然好很多,但在我们上学那会儿,完全是混混沌沌,不知道以后毕业了去干嘛,当人家很好奇地问起自己的专业时,也很难用只言片语跟人家描述清楚,那种学了n年还说不清自己专业的羞愧呐。。。直到后来Google Map、Google Earth横空出世,当大家发现这玩意儿能在电脑上看到自己家房顶,找到玩转世界那种“君临天下”的感觉的时候,我们终于可以傲娇地说,俺的专业就是做这个的lol(其实你懂得)。
当我们去查询GIS的概念,一般都会这样介绍——“在计算机软硬件的支持下,对地理数据进行获取、存储、分析、显示、输出的信息系统。”
“那GIS不就是用计算机做地图吗?”
“GIS比计算机制图高级,因为我们有数据库支撑,我们还可以做空间分析……”
听起来无所不能的GIS,但在很长时间里其实也只是停留在做出专题图的阶段,像图1中的渐变色就很清晰的显示出各省的男同胞的平均身高,各位可以很迅速地在心里得出自己有木有拖后腿的结论,再或者可以跟地图交互查询一下属性,压根儿用不到复杂的空间分析。
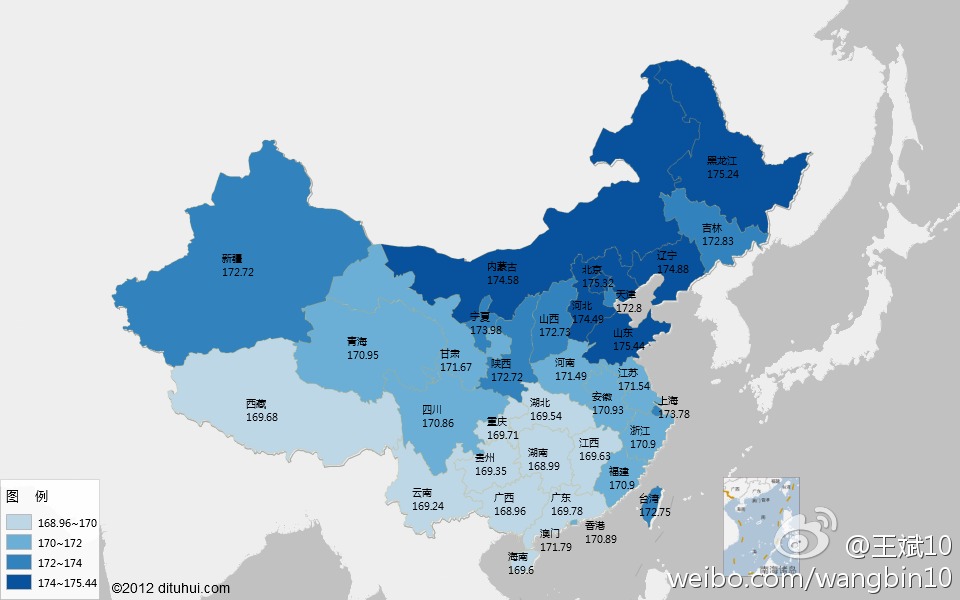
图1 中国各省男性平均身高
那GIS究竟能做什么呢?首先就是收集地理信息,人类活动75%都与地理位置有关,比如想和男朋友找个电影院看电影,出差到一个陌生的城市找宾馆,这些都是地理信息,通过GIS能有效地把这些都存储起来,怎么存呢?excel吗?那怎么和地图关联起来?这是后话,当然这些问题不太用我们用户操心,业界大佬们早就定义好了地理信息的各种存储方式,文件抑或数据库都可以,我们只要按要求把信息录入就可以了。
收集到的地理信息,现在也只是电脑中的一堆表格,那怎么为人们所看到呢?这就是所谓的“可视化”了,各种图表是信息可视化的产物,那地理信息可视化的产物就是“地图”,当然地图远比GIS出现的要早,这位前辈是GIS重要的代言人,GIS可以方便地将收集到的信息在地图上展示,如图1用深浅变化的颜色表达身材的高低,如果收集到的信息还有女性的身高,分分钟就可以再做出一幅类似的女性身高图来。而即使你是一个绘图高手,可以在CorelDraw、Illustrator甚至Photoshop中绘制出图1,但却很难再此基础上立刻绘制出另一幅女性身高图来。
而空间分析其实离我们也并不遥远,像大众点评这样的应用已经相当普及,我可以很方便地找到周边的餐馆,还有地图导航,都是通过GPS装置收集的你的地理位置之后,在地图上找到正确的位置显示,再进一步的实现诸如查询搜索等功能。
2. 数据:有料才是王道
大体知道了GIS是什么,我们再来讨论下图1是怎么做出来的,身高之类的数据很好收集得到,可是地图呢?让我们追根溯源地想一想地图究竟是怎么画出来的,在没有测绘,没有RS,没有GPS的年代,我们的老祖先们就是靠脚步来丈量土地,靠眼睛看到的来手绘地图,而现在RS可以通过卫星来给地球拍照,GPS可以实时定位,虽然已经摆脱了“数据基本靠走”的时代,但是想得到数据还是要花费些代价,大多数地理数据还没有开放需要购买,当然像图1中这样比例尺级别(第4部分我们会讨论到)的地图,还是很容易从网上得到,那我们下载后,就可以在GIS软件中打开,将身高数据录入,从而快速的做出一幅地图来。
所谓“巧妇难为无米之炊”,数据才是王道,否则GIS系统就是一个空架子。对于数据而言,GIS有两大基本存储模型,一种是矢量数据模型,一种是栅格数据模型。如图2所示,同样信息的表达,在左边的矢量数据中,我们看到的是清晰的点、线、面的实体,来表达河流、湖泊、地块这样的信息;而右边的栅格数据中,我们看到的则是一个个的格子,相相同的像元值在地图上展示出相同的颜色,从而也呈现出河流、湖泊、地块的形态。虽然都能表达出一样的信息,但是这两种存储模型是完全不同的,矢量是以对象为单位,我们可以把一个湖泊的面积等属性都存储在该对象中;而用栅格表达的话,湖泊是由一组像元组成的,我们不可能将整个湖泊的面积分别赋予每个像元。
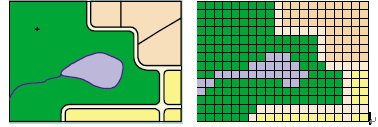
图2 矢量数据模型与栅格数据模型
网上公开免费的数据哪里可以下到呢?在美国数据的开放程度还是相当高的,像人口普查之类的详细数据完全可以获取到(http://thistract.com/),另外还有一些网站可以获取数据:
全球90m分辨率的DEM(高程数据)下载:
http://srtm.csi.cgiar.org/index.asp
Natural Earth提供了全球1:10 000 000、1:50 000 000、1:110 000 000比例尺的矢量和栅格数据下载,格式为ESRI的shp、Geodatabase以及tiff:
http://www.naturalearthdata.com
Bathymetry是海洋深度的测量数据,在 British Oceanographic Data Centre 的网站上可以下到全球海洋深度数据:
Globe land cover facility提供免费卫星图像,如Landsat、 Modis、 Ikonos、 Quickbird等,下载地址:
对于中国用户,开放的免费数据获取途径有限,国家基础地理信息中心发布过全国1:400万比例尺的矢量图,详细到县级行政数据。另外,如果我们只是需要背景地图显示的话,可以不必获取原始数据,而采用叠加地图服务的方式。中国的ArcGIS Online(http://www.arcgisonline.cn)为中国用户提供了免费的地图服务,我们只需要将其与我们的数据叠加,就可以快速做出一幅地图来,当然这里的地图服务不能够直接进行查询,它的作用类似于背景图片。
3. 比例尺:地图的亲密爱人
早在晋代制图学家裴秀就提出“制图六体”的概念:分率、准望、道里、高下、方邪、迂直,首当其冲的分率指的就是比例尺。无论是我们购买的地形图,还是我们在软件中出图,都要涉及到比例尺,对于地图而言,比例尺是不可或缺的亲密爱人。就像上节中我们提到Natural Earth提供了全球1:10 000 000的矢量数据下载,这里的1:10 000 000就是比例尺,它的含义是:地图上任意线段长度与它代表的实地水平距离之比,也就是说如果地图上两点之间测量的距离为1mm,那么实地的距离则是10km。
简单来讲,地图都是对现实世界的抽象缩小,比例尺就代表了抽象的程度。比例尺越小,抽象程度越高,表达的地物就少而简单;比例尺越大,抽象程度低,表达的地物就越详细。如图3所示,同一个湖泊在较大比例地图上以面来表示,可以看到湖泊的轮廓,而在较小比例尺地图上就只是以线来表示。这个对地物进行抽象的过程存在于数据采集这个环节,对于采集到的数据,在软件中我们是可以实现比例尺的无极缩放的,这时候改变的就不再是抽象程度,而是显示的地理范围了。
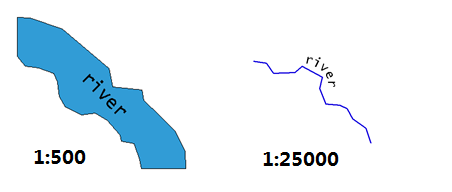
图3 不同比例尺对于地物的抽象程度
我国规定1:5千、1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万、1:100万八种比例尺地形图为国家基本比例尺地形图。编制这些地图要么通过全站仪、经纬仪等大地测量的方式,要么通过航摄的方式。因此这里又要引入两个概念:测图比例尺和航摄比例尺。由于人眼在地图上的分辨率通常为0.1mm,不同比例尺图上0.1mm所代表的实地距离,称为地形图比例尺的精度,该精度决定了测图比例尺。例如,某工程测量要能够在图上表达出10cm的精度,则选取的测图比例尺应不小于0.1mm/10cm=1/1000。航摄比例尺与成图比例尺的关系见下表(影像分辨率指的是影像所能识别出的最小地物单元的大小)
表1 成图比例尺与航摄比例尺及影像分辨率关系
|
成图比例尺 |
航摄比例尺 |
影像分辨率(m) |
|
1:500 |
1:2000-1:3000 |
0.05 |
|
1:1000 |
1:3500-1:4000 |
0.1 |
|
1:2000 |
1:6000-1:8000 |
0.2 |
|
1:5000 |
1:10000-1:20000 |
0.4-0.8 |
通过上表中的对比,我们可以发现成图比例尺基本是航摄比例尺的4倍,为什么是4倍,原因是精度决定,4倍内的摄影照片就够了,刚好不会出现马赛克,如果将摄影比例尺确定得过小,造成图像模糊不清,甚至出现“马赛克”图案,影响成图质量;反之,将摄影比例尺确定得太大,“大材小用”造成不必要的资源浪费。
4. 坐标:究竟有多重要
很多时候碰到学员拿来这样的数据,坐标值不正确或者没有坐标系,无法和其他数据正确的叠加在一起显示,无法设置比例尺,也无法做拓扑检查之类的工作。坐标不正确的原因主要有:在用CAD等软件作图的时候没有设立好正确的地理坐标系,或者数字化纸质地形图或影像的时候没有注意是否经过配准这一步骤;坐标系缺失的情况就更多了,导入数据的时候只导入了坐标值信息,或者数据格式转换的时候忘记了指定坐标系。
而一个地物怎样才能正确定位在地球上?答案是正确的坐标值加上坐标单位。让我们暂时抛开地球是个三维球体,先来完成在平面图上画出一栋房子的任务,现在知道房子的几个拐点坐标(1,1)(3,1)(3,4)(1,4)。首先我们必须要先确认的是坐标原点在哪里?其次还要有横轴和纵轴以及单位刻度(房子的长宽是米,现在坐标轴的刻度单位也是米),那图4中所示的就是房子应该在的位置。而地理数据定位也是同样的原理,只不过大地坐标系的定义则是:以参考椭球体(用来模拟地球的光滑球体)中心为原点,本初子午面(英国格林尼治天文台所在位置为本初子午线,即0度经线)为纵轴方向,赤道平面为横轴方向,如图5所示,红色点的坐标就应该是(50,40),单位为度。
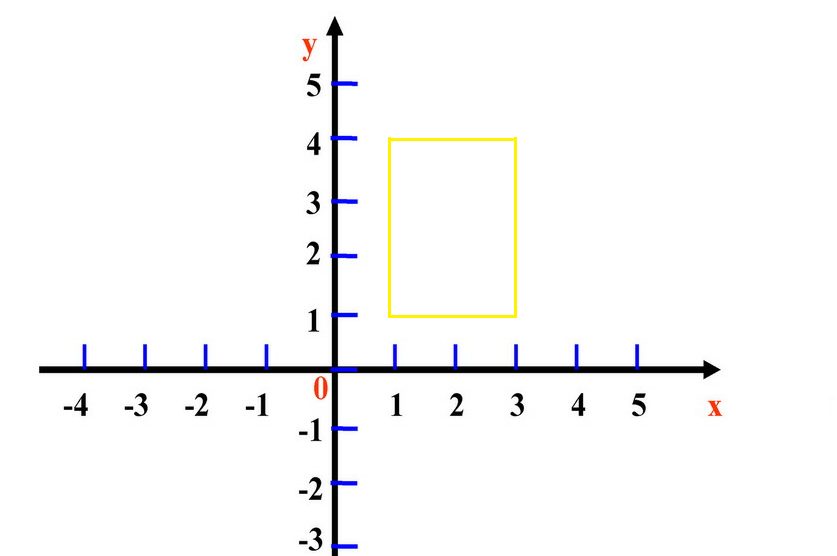
图4 二维笛卡尔坐标系
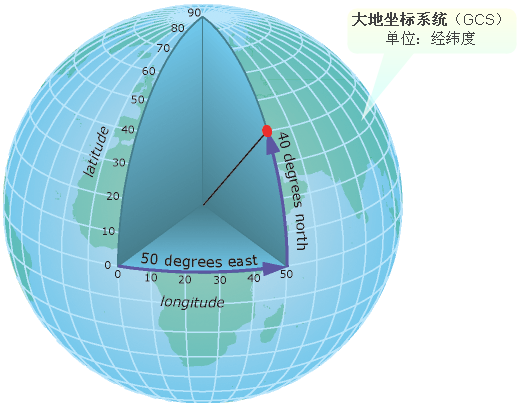
图5 大地坐标系
获取正确的地理坐标究竟有多么重要?是不是我做一幅地图所需的数据必须要知道正确的地理坐标呢?我们知道获取坐标并不是一件相当容易的事情,草根的方法通常是在Google Earth上添加地标,通过KML这种格式导入GIS软件生成矢量图,官方的途径就是通过购买了。但其实某些时候,坐标并不是我们所认为的那么重要,比如我要做景观分析,研究一个村落的布局,在此基础上做一些地图,我想说,其实你真的不必为地理坐标困扰,找一个航拍图片,没有的话纸质地图也可以,直接在上面描图获得数据,就像小时候大家大概都撕过课本封面上的透明薄膜叠在其他图上描图,原理是一样的,只是你这时获取的坐标是相对坐标罢了,既然我不需要和其他地图叠加在一起定位,我又何必要关心地球坐标原点在哪里呢?
5. 投影:神马不是浮云
我们知道地球是一个形状不规则的椭球体,那如果为地球画一张平面画像,那该如何尽可能真实地再现地球的真实面貌呢?前面我们了解到地理坐标系的定义:以球心为坐标原点,东西方向按经度划分为360度,南北方向按纬度划分为180度,也就是我们所说的WGS(大地坐标系)将地物进行还原,如图6即是按经纬度直接描绘出的世界地图。
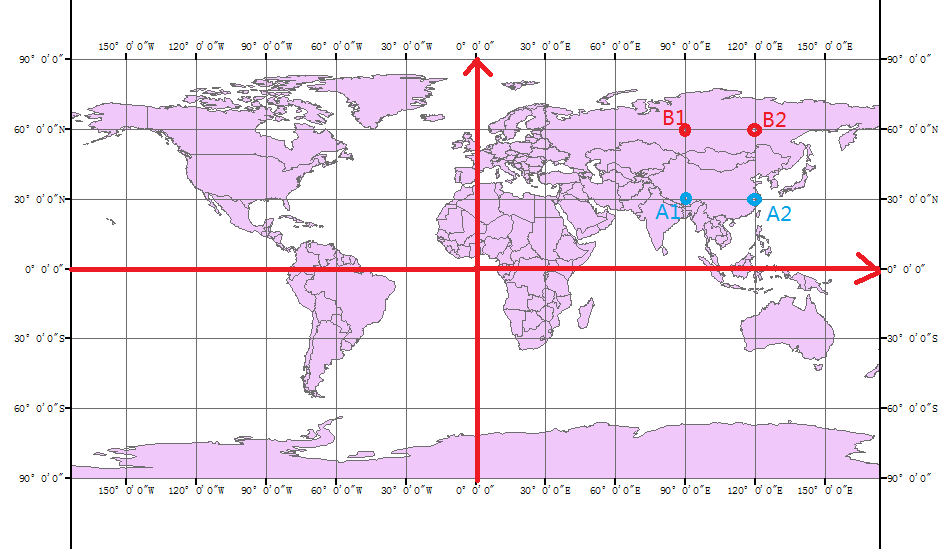
图6 未投影的世界
一切看起来都很正常,正如有本书所写“世界是平的”,但我们仔细一看就会发现问题,A1A2之间的距离和B1B2之间的距离在图上看起来是相等的,但是实际上,位于不同纬度的相同经度差绝对是不相等的,位于赤道上的距离远比位于两极的要大很多,因此用上面提到的画像方式来做平面地图是不能很好地表达距离,方向之间的相对位置关系的,所以我们在制图的时候才要引入投影,即将三维球面展现到平面地图上,对于地图来讲,投影绝对不是浮云。

图7 Albers投影
这里我们选取了Albers(等积圆锥投影),世界地图立马呈现出不一样的形态,这里A1A2和B1B2之间的距离也发生了变形,因为投影是三维向二维的映射,所以必然会产生变形,我们可以为不同用途的地图选取相应的投影方式来保证面积,方向或角度的变形最小。