跳台阶

题目：（1）一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。

分析：当n = 1， 只有1中跳法；当n = 2时，有两种跳法；当n = 3 时，有3种跳法；当n = 4时，有5种跳法；当n = 5时，有8种跳法；

n	1	2	3	4	5	6	7	8	9	10
sum	1	2	3	5	8	13	21	34	55	89

规律如下：

f(n)=f(n-1)+f(n-2)

首先考虑简单的情况

只有一个台阶的时候只有一种跳法

两个台阶时有两种跳法。

对于有n阶楼梯时，有f(n)种跳法，假设先跳一个台阶，则剩下n-1个台阶，就还有f(n-1)中跳法，假设先跳两个台阶，则剩下n-2个台阶，就还有f(n-2)中跳法。

由此可以推导出，对于一个n阶楼梯：

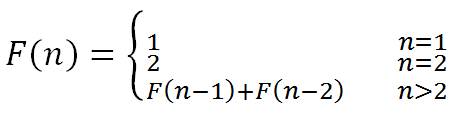
 代码如下：

#include "stdio.h"
#include "stdlib.h"
  
int function(int n);
  
int main(void)
{
  int tmp;
    
  tmp = function(10);
  printf("%3d
",tmp);
  
  return 0;
}
  
int function(int n)
{
  if(n == 1)
    return 1;
  else if(n == 2)
    return 2;
  else 
    return function(n-1) + function(n-2);
}