最近学校那边已经结业,在家闲来无事,便开始在牛客网上开始刷题,在线编程的题目有些自己还做不了,不过有些题直接解决以后再看看讨论区大神的答案,只能感慨还有这种操作,所以这篇博客就来记录一下这些神一般的操作。
1、判断一个数是否是素数
素数(也叫质数):即只能被1和自己本身整除的数。这里有几种判断方法。
(1)直接判断法
根据定义直接判断从2到n-1是否存在n的约数即可。
public static boolean isPrime(int n){
for (int i = 2; i < n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
(2)直接判断法改进
上述的方法,存在效率低的问题,对于一个数n,其实并不需要从2判断到n-1。这里有一个小知识点就是,若一个数可以分解质因数,那么分解得到的两个数一定是一个小于根号n,另一个大于根号n。所以只需判断从2到根号n之间是否存在约数。若根号n左边找不到约数,那么右边一定也找不到。
public static boolean isPrime(int n){
for (int i = 2; i < Math.sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
(3)6的倍数法
首先看一下关于质数分布的规律:大于等于5的质数一定和6的倍数相邻。例如5和7,11和13,17和19等。
证明:令x ≥ 1,将大于等于5的自然数表示如下:
... 6x-1,6x,6x+1,6x+2,6x+3,6x+4,6x+5,6(x+1),6(x+1)+1 ...
可以看到不在6的倍数两侧的数,6x+2,6x+3,6x+4,由于2(3x+1),3(2x+1),2(3x+2)一定不是素数,再除去6x本身,即素数只能出现在6x相邻的两侧。但是这个方法不是绝对的,在6的倍数相邻的两侧并不一定就是素数。注意:素数出现在6x两侧 ≠ 6x两侧都是素数
根据以上规律,判断质数可以以6个为单元快进。
public static boolean isPrime3(int n){
//判断较小的数
if (n == 2 || n == 3) {
return true;
}
//不是6x两侧的数一定不是素数
if (n % 6 != 1 && n % 6 != 5) {
return false;
}
//在6x两侧是也不一定都是素数
for (int i = 5; i <= Math.sqrt(n); i+=6) {
if (n % i == 0 || n % (i+2) == 0) {
return false;
}
}
//排除所有,剩下的都是素数
return true;
}
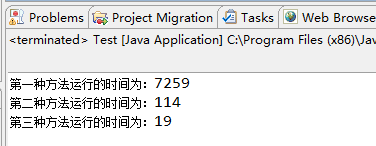
性能测试:数据量为20W
public class test {
public static void main(String[] args) {
long s1 = System.currentTimeMillis();
for (int i = 0; i < 200000; i++) {
isPrime(i);
}
long s2 = System.currentTimeMillis();
System.out.println("第一种方法运行的时间为:"+(s2-s1));
long s3 = System.currentTimeMillis();
for (int i = 0; i < 200000; i++) {
isPrime2(i);
}
long s4 = System.currentTimeMillis();
System.out.println("第二种方法运行的时间为:"+(s4-s3));
long s5 = System.currentTimeMillis();
for (int i = 0; i < 200000; i++) {
isPrime3(i);
}
long s6 = System.currentTimeMillis();
System.out.println("第三种方法运行的时间为:"+(s6-s5));
}
//方法一
public static boolean isPrime(int n){
for (int i = 2; i < n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
//方法二
public static boolean isPrime2(int n){
for (int i = 2; i < Math.sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
//方法三
public static boolean isPrime3(int n){
//判断较小的数
if (n == 2 || n == 3) {
return true;
}
//不是6x两侧的数一定不是素数
if (n % 6 != 1 && n % 6 != 5) {
return false;
}
//在6x两侧是也不一定都是素数
for (int i = 5; i <= Math.sqrt(n); i+=6) {
if (n % i == 0 || n % (i+2) == 0) {
return false;
}
}
//排除所有,剩下的都是素数
return true;
}
}
程序运行的结果为:
2、字符替换
对于字符串的操作,有一种很便捷的方法就是使用正则表达式,String中也提供了有关正则表达式的方法。
①matches(String regex)
返回boolean,字符串匹配的方法
②replaceAll(String regex,String replacement)
返回String,字符串替换的方法
③split(String regex)
返回String[],字符串拆分的方法。
例一:删除一串字符中的数字
public static void main(String[] args) {
String str = "1s2f3v4s5hj6x7hj8sdr";
System.out.println(str.replaceAll("\d", ""));
}
程序输出的结果是:sfvshjxhjsdr
正则表达式中d表示的是数字,D表示的是非数字。
例二:输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。例如,输入”They are students.”和”aeiou”,则删除之后的第一个字符串变成”Thy r stdnts.”
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str1 = in.nextLine();
String str2 = in.nextLine();
in.close();
String pattern = "[" + str2 + "]";
String s = str1.replaceAll(pattern, "");
System.out.println(s);
}
例三:将一句话的单词进行倒置,标点不倒置。比如 I like beijing. 经过函数后变为:beijing. like I
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str = in.nextLine();
in.close();
String out = "";
String[] s = str.split(" ");
for (int i = s.length-1; i >= 0; i--) {
out += s[i] + " ";
}
System.out.print(out.trim());
}
3、字符串中找出连续最长的数字串
刚开始见到这个题的时候,我的思路为:
(1)先将这个字符串进行预处理,根据非数字字符将字符串分割成数字串数组;
(2)遍历这个数字串数组,比较每个数字串的长度,将最长数字串进行输出。
代码如下:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str = in.nextLine();
in.close();
String[] n = str.split("\D");
int max = 0;
String out = "";
for (int i = 0; i < n.length; i++) {
if (n[i].length() > max) {
max = n[i].length();
out = n[i];
}
}
System.out.println(out);
}
运行通过之后,在讨论区见到一种全新的方法,算法思想如下:
(1)定义一个max表示经过的数字的长度的最大值,count表示计数器,当为字母时重置为0;
(2)定义end表示数字尾部,每次满足数字时,对max进行判断,当max小于count时,更新max和count;
(3)最后使用String的substring(begin, end)进行输出,不包括end,从begin取到end - 1。
public static void main2(String str){
int max = 0;
int count = 0;
int end = 0;
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) >= '0' && str.charAt(i) <= '9') {
count++;
if (max < count) {
max = count;
end = i;
}
}else{
count = 0;
}
}
System.out.println(str.substring(end-max+1, end+1));
}
4、求n!(即阶乘)末尾有多少个0?
比如: n = 10; n! = 3628800,所以答案为2。
刚开始见到这题的时候,就直想着计算阶乘,老老实实计算0的个数,碰到的问题是,n的范围很大,从1到1000,超出了普通类型的最大值,因为之前用过BigInteger这个类,所以就想到用BigInteger来表示阶乘的值。代码如下:
import java.math.BigInteger;
import java.util.Scanner;
public class Main9 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
in.close();
String num = String.valueOf(jiecheng(n));
char[] c = num.toCharArray();
int count = 0;
for (int i = c.length-1; i > 0; i--) {
if (c[i] == '0') {
count++;
}else{
break;
}
}
System.out.println(count);
}
public static BigInteger jiecheng(int i){
int sum = 1;
BigInteger bigsum = BigInteger.valueOf(sum);
for (int j = i; j >0 ; j--) {
BigInteger bigj = BigInteger.valueOf(j);
bigsum = bigsum.multiply(bigj);
}
return bigsum;
}
}
运行之后,还是通过了检测,但是从感觉这道题肯定不是像我这么解决的,到讨论区一看之后,全是什么分解质因数,计算5的个数,懵了,以为题不对应,看到半天才讨论区的方法才是最简洁的。
算法思路:
(1)一个数 n 的阶乘末尾有多少个 0 取决于从 1 到 n 的各个数的因子中 2 和 5 的个数而 2 的个数是远远多余 5 的个数的,因此求出 5 的个数即可;
(2)求解因子 5 的个数的方法是用 n 不断除以 5,直到结果为 0,然后把中间得到的结果累加. 例如, 100/5 = 20, 20/5 = 4, 4/5 = 0。则 1 到 100 中因子 5 的个数为 (20 + 4 + 0) = 24 个。即 100 的阶乘末尾有 24 个 0。
其实不断除以 5,是因为每间隔 5 个数有一个数可以被 5 整除, 然后在这些可被 5 整除的数中每间隔 5 个数又有一个可以被 25 整除, 故要再除一次, ... 直到结果为 0, 表示没有能继续被 5 整除的数了。
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
in.close();
int count = 0;
for (int i = 1; i <= n; i++) {
int temp = i;
while (temp%5 == 0) {
count++;
temp /= 5;
}
}
System.out.println(count);
}
参考博客
[1]判断一个数是否为质数/素数——从普通判断算法到高效判断算法思路
http://blog.csdn.net/huang_miao_xin/article/details/51331710