BUPT T1:
第一场比赛。
目前已掌握:CDEFGHIJ
C:给定一颗有根树,树上每个节点有权值和颜色。有两种操作。一种是修改某个节点的颜色,一种是修改某个节点的权值。每次操作结束后要你回答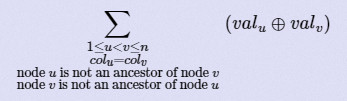 。
。
思路:首先我们想到不是祖先这个过程比较难以处理,我们不妨考虑问题的反面,就是两个点颜色相同且互为祖先。那么修改一个点对答案的贡献显然了。一个是这个点所在的子树的同颜色的节点个数,还有一个是这个点到根的同颜色节点个数。点到根这个地方如果采用树剖的话,复杂度过高,我们不妨考虑子树加单点查来实现维护根路径点数。显然颜色与颜色之间是独立的,所以我们可以对每个颜色离线处理。然后调了1w年之后写了发线段树,TLE。发现是因为线段树有pushdown导致速度过慢。我们考虑子树加单点查改为差分前缀和后的单点修改区间查,就可以使用飞快的树状数组通过本题。(树状数组还是赛后翻题解才想到的呜呜呜)
D:有n个数,每次可以合并相邻的两个数,变为这两个数的和,尽量构造一个答案使得结果中a的倍数的数尽量的多。
思路:非常简单的DP题,对数组进行前缀和之后,我们每次只要从last[sum[i]%a]处转移即可
E:有n个人,每次将两个人联系在一起,求每次操作之后,取出任意三个人使得三个人没有任意两人在同一个联通块的方案数。
思路:队友的思路是倒着做,然后每次删除一条边考虑会新产生的贡献。实际上正着做也是可以的,假设A与B联通,每次连边时答案减少的就是|A|*|B|*(n-|A|-|B|)
F:给定l,r求l,r内数字x为数位众数的方案数。
思路:这题作为数位DP菜鸡是肯定不会的,后续研究了数学大佬队友的做法才勉强明白。第一就是众数这个东西定义比较模糊,我们不妨考虑枚举数字x出现了多少次,然后其他的数字就可以利用背包填上了,填背包的时候保证每个数字使用不会使它成为众数即可。之后要做好准备特训一下数位DP了(未重写)
G:给定n个点的完全图,图的边权随机,求删除k条边后最短路的最大长度。
思路:随机的东西就考虑暴力了。显然每次删除必须在最短路上。每次暴力跑最短路,然后暴力枚举删除即可。复杂度不会证。但是据赛后对题解的阅读说是期望在3左右?毕竟脑子太差想不出来更强大的做法了。
H:给定一个点的初始位置和x,y速度,求点与边界第n次碰撞的时间。
思路:这题赛中并没有任何想法,大概都是队友提供的思路。首先考虑碰撞可以变成三角形对碰撞边对称,然后问题转化为交点问题。我们考虑速度*时间长度内,该线与三条平行线的交点个数。那么与x轴平行显然非常好求,直接dy/(Lsqrt(3)/2)就得到了,其他方向可以通过旋转速度向量来得到答案。由于是第一次ACM,没准备板子,直接去网络上拷了个计算几何的板子代码改了改交的。下次尽量避免0.0(其实就是旋转速度向量不会写,我知道我菜了呜呜呜)
I:给定一个括号和"?"组成的序列。"?"可以变成“(”“)”或者直接删除,求字典序最小的合法括号序列。长度第一,字典序第二
思路:队友做的,赛后看了一下题目,这一看就是贪心啊QAQ,因为长度要尽量小,那就是从最左边的"?"匹配完最左边无法匹配的右括号,最右边匹配完无法匹配的左括号,然后其余全部删除即可
J:有两个人在坐标轴上移动,每次可以选择一个人移动到下一个目标点。然后要求最小化代价和,代价为两个坐标直接的曼哈顿距离。
思路:这题赛中不会,虽然式子很显然是f[i][j]=f[i-1][j]+dis(i,i-1),f[i][i-1]=f[i-1][k]+dis(k,i),但是并不会优化。然后赛后看了题解觉得是真的妙(。我们发现dis(i-1,i)是定值,也就是相当于每次DP数组中每段都固定加上一个定值,我们就可以把这个定值提出来,变成除了f[i][i-1]那个位置需要特殊转移的情况下,其他点不变。这样f[i][i-1]=f[i-1][k]+dis(k,i)-dis(i-1,i)。那么这时候第一维已经可以去掉了,我们只需要找f[k]+dis(k,i)min即可。本来订正的时候看到kdtree都劝退了,但是本着作为以后队内很可能要打数据结构的菜鸡还是做了一下。几乎是对着标程抄的,因为是维护DP数组还要替罪羊重构。写了很多次都没写出来,后来老老实实抄着标程写,实在是太自闭了,主要是在以前指学过理论的前提下加上一个只学了一天的kdtree写,后来发现其实可以把dis暴力拆成abs,利用树套树或者cdq+扫描线+线段树来分成四块来查找和维护(cdq已经要忘光了,我之后就补呜呜呜),树套树姑且还是没问题的,所以目前就写了kdtree版本(待填)。