(题目在文末)
T1.qiang
不写逆元见祖宗..
首先一个合法方案最少要包含一个形如1,2,3,..n的数列,再考虑在其中插入一些数。
考虑以x结尾的一种方案,x贡献了了num[x]次,在初始序列中出现了一次,所以贡献了num[x]-1次,其中的每一种,都有sum[x]-1个地方可以放(至少放在x前,不然就违背了定义)
所以答案就是π(C(sum[i]-1,num[i]-1))(之前都想得很正常,接下来开始表演爆0)
具体计算组合数时,显然要预处理阶乘,然而这里有乘法,所以要用逆元(这不是显然吗,我的脑子呢..)

#include<iostream> #include<cstdio> using namespace std; const int MAXN=500005; const int N=500000; const int MOD=998244353; typedef long long ll; inline ll rd(){ ll ret=0,f=1;char c; while(c=getchar(),!isdigit(c))f=c=='-'?-1:1; while(isdigit(c))ret=ret*10+c-'0',c=getchar(); return ret*f; } ll po(ll x,ll y) { ll ret=1,base=x; while(y) { if(y&1) (ret*=base)%=MOD; (base*=base)%=MOD; y>>=1; } return ret; } ll fac[MAXN],inv[MAXN]; void prework() { fac[0]=1; for(int i=1; i<=N; i++) fac[i]=(fac[i-1]*i)%MOD; inv[N]=po(fac[N],MOD-2); for(int i=N-1; i>=0; i--) inv[i]=(inv[i+1]*(i+1))%MOD; } inline ll C(ll x,ll y){ if(y>x) return 0; return (1ll*(fac[x]*inv[y])%MOD*inv[x-y])%MOD; } ll ans=1; ll n; ll num[MAXN],sum[MAXN]; int main() { prework(); n=rd(); for(int i=1;i<=n;i++) num[i]=rd(),sum[i]=sum[i-1]+num[i]; for(int i=1;i<=n;i++){ ans*=C(sum[i]-1,num[i]-1); ans%=MOD; } cout<<ans<<endl; return 0; }
T2.count
30分:朴素状压 O(4*T*(2^n))
60分:行列交换之后状压,复杂度O(T*n*256) (数据水,其实这里就能拿100分了)
100分:对于状压的两个可行状态i和j,且i可以向j转移,那么在i和j之间连边,把原问题转化为在图上走n步到达制定状态的问题。
邻接矩阵存图,矩阵乘法。
或者是归纳出一个神奇的公式f(n)=f(n-1)+5*f(n-2)+f(n-3)-f(n-4)
60分做法:

#include<iostream> #include<cstring> #include<cstdio> using namespace std; int f[100005][18]; const int UP=(1<<4)-1; bool legal[32]; int n,m; void prework(){ for(int i=0;i<=UP;i++){ int cnt=0,succ=0; for(int j=0;j<4;j++){ if(i&(1<<j)) {if(cnt&1) break;cnt=0;} else cnt++; } succ=1; if(cnt&1) continue; legal[i]=succ; } } int main(){ prework(); int T; while(cin>>n>>m){ if(!n) return 0; memset(f,0,sizeof(f)); f[0][0]=1; for(int i=1;i<=n;i++){ for(int j=0;j<=UP;j++){ if(!legal[j]) continue; for(int k=0;k<=UP;k++){ if(!legal[k|j]) continue; if(j&k) continue; f[i][j]+=f[i-1][k]; f[i][j]%=m; } } } cout<<f[n][0]<<endl; } return 0; }
100分做法:

#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int MAXN=32; const int UP=16; int MOD; struct Mat { int data[MAXN][MAXN]; Mat() {memset(data,0,sizeof(data));} Mat operator*(const Mat &rhs) { Mat ret; for(int k=0; k<UP; k++) for(int i=0; i<UP; i++) for(int j=0; j<UP; j++) ret.data[i][j]+=data[i][k]*rhs.data[k][j],// ret.data[i][j]%=MOD; return ret; } }; Mat pow(Mat y,int x) { Mat ret,base=y; for(int i=0; i<UP; i++) ret.data[i][i]=1; while(x) { if(x&1) ret=ret*base; base=base*base;x>>=1; } return ret; } int legal[MAXN]; void prework() { for(int i=0; i<=UP; i++) { int cnt=0,succ=0; for(int j=0; j<4; j++) { if(i&(1<<j)) { if(cnt&1) break; cnt=0; } else cnt++; } succ=1; if(cnt&1) continue; legal[i]=succ; } } Mat sav,ori; int n; int main() { prework(); for(int i=0; i<UP; i++) { for(int j=0; j<UP; j++) { if(!legal[i|j]) continue; if(i&j) continue; ori.data[i][j]=1; } } while(cin>>n>>MOD) { if(!n) break; Mat tmp=pow(ori,n-1); int ans=0; for(int i=0; i<UP; i++) if(legal[i]) ans+=tmp.data[0][i]; cout<<ans%MOD<<endl; } return 0; }
T3.sequence
理解是这样的,先考虑一个弱化版本,如果不是mod 4意义下呢?
假设B[i]>A[i],那么每个A[i]需要增加C[i]=B[i]-A[i],不妨处理出这个C[i]
比如,我们有A[]={0,3,1,2,1},B[]={3,7,8,6,8},那么可以算出C[]={3,4,7,4,7},不妨看成一个柱状图
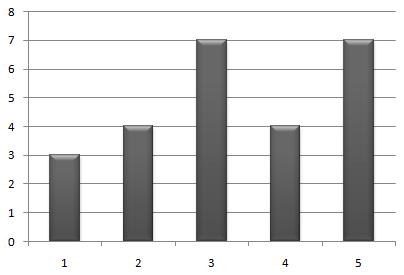
区间整体加1,可以看成横向削一层,不难发现答案就是Σmax(0,a[i]-a[i-1])
这启发我们在考虑mod 4意义下的问题时,也另外考虑一个差分数组d(diff)[i]
对原区间进行区间加,就是差分数组的单点修改,考虑一个区间[i,j],我们要做的就是d[i]++,d[j]--
现在就来考虑一下如何贪心地给d[j]寻找一个对应的d[i],使得配对代价最小。
用一个桶维护前面出现过的数,并只计算正数的贡献(max(0,x)),贪心地从小往大选

#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int MAXN=1e7+10; int a[MAXN],b[MAXN],c[MAXN],d[MAXN],s[MAXN]; int n; int main(){ int T; cin>>T; while(T--){ cin>>n; memset(s,0,sizeof(s)); for(int i=1;i<=n;i++) cin>>a[i]; for(int i=1;i<=n;i++) cin>>b[i]; for(int i=1;i<=n;i++) c[i]=(b[i]-a[i]+4)%4; for(int i=1;i<=n;i++) d[i]=c[i]-c[i-1]; int ans=c[1],j; for(int i=2;i<=n;i++){ s[(d[i]+3)%4+1]++; if(d[i]<=0) continue; for(j=0;!s[j];j++); s[j]--; ans+=j; } cout<<ans<<endl; } return 0; }
官方题解




