[LUOGU] P2704 炮兵阵地

题目描述
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。  
一个N*M的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），  
也可能是平原（用“P”表示），  
如下图。在每一格平原地形上最多可以布置一支炮兵部队  
（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

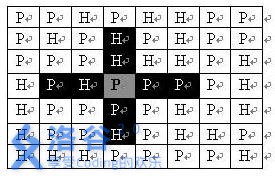
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入输出格式
输入格式：
第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。

输出格式：
仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

输入输出样例
输入样例#1： 
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例#1： 
6

真的很强了这个题
好好地理解了状压DP

预处理以下
1. 二进制数的1个数（统计答案）cnt数组
2. 二进制数两个1之间距离是否小于2(防止同一行打架）fight数组
3. 二进制数是否有1和输入的山对上(&结果为1) x&std_line[i]

cnt数组可以方便地由之前的状态转移，和之前的题一样的思路。

最初是三维状态f[i][j][k] 第i行 状态j 前一行状态k
然后枚举前一行和前前行的状态，转移，加上 cnt[这行状态]
但是100*1024*1024 显然炸了，转移时间1024*1024*1024*100 飞了

考虑对压缩的状态继续进行压缩（离散化？）

尝试输出了仅仅符合预处理2（同一行不打架的） 在m=10时也仅有60种放置方案

也就是说，二三维开60，对应到数组okset[i]j存储对应可用状态
可以用哨兵(okset[i][0])存储大小（类似vector.size()），不过我单独拿出来siz数组存了
毕竟，一堆堆方括号不好看（二维邻接表的教训）
这样空间绰绰有余（预处理3可能进一步减小数据量）

不过要注意的是边界问题，第1行单独拿出来处理（别忘了统计ans，否则若n==1就挂了）
f[1][i][1~60] 均为cnt[okset[1][i]]

//Stay foolish,stay hungry,stay young,stay simple
#include<iostream>
#include<vector>
#include<cstdio>
using namespace std;

const int MAXN=105,L=11;

int n,m;

bool map[MAXN][L];
int std_line[MAXN],fight[1026];
int cnt[1026];
int f[MAXN][61][61];
int okset[MAXN][61];
int siz[MAXN];
char s[L];

void debug(int x){
    for(int i=10;i>=0;i--) {
        cout<<((x>>i)&1);
    }
    cout<<endl;
}

int main(){
    cin>>n>>m;
    getchar();//
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        for(int j=1;j<=m;j++){
            map[i][j]=s[j]-'P';
            std_line[i]|=(map[i][j]<<(j-1));
        }
    }
    for(int i=0;i<(1<<m);i++){
        cnt[i]=cnt[i>>1]+(i&1);
        int v=(i<<2);
        int cnt0=0;
        while(v){
            if(v&1){
                if(cnt0<2) {fight[i]=1; break;}
                cnt0=0;
            }else{cnt0++;}
            v>>=1;
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=0;j<(1<<m);j++){
            if((j&std_line[i])==0&&!fight[j]) {
                okset[i][++siz[i]]=j;
            }
        }
    }
    int ans=0;
    for(int i=1;i<=siz[1];i++){
        for(int j=1;j<=60;j++){
            f[1][i][j]=cnt[okset[1][i]];
        }
    }
    siz[0]=1;
    for(int i=2;i<=n;i++){
        for(int x=1;x<=siz[i];x++){
            for(int y=1;y<=siz[i-1];y++){
                for(int z=1;z<=siz[i-2];z++){
                    int j=okset[i][x],k=okset[i-1][y],l=okset[i-2][z];
                    if(((j&k)!=0)||((j&l)!=0)||((k&l)!=0)) continue;
//                  cout<<"ID:"<<i<<endl;
//                  debug(j);debug(k);debug(l);
//                  cout<<"F:";
                    f[i][x][y]=max(f[i][x][y],f[i-1][y][z]+cnt[j]);
//                  cout<<f[i][x][y]<<endl;
                    ans=max(ans,f[i][x][y]);
                }
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}