Radiance Fields
The Radiance Field – Nathan Reed’s coding blog (reedbeta.com)
CMU 15462 Slide
Neural Radiance Fields (NeRF)
前置知识
目的
量化光的测量
如何量化光强
对于一些光子:
- Radiant energy: 碰撞总数
- Radiant flux: 每秒碰撞数
- Irradiance: 每秒每单位面积碰撞数
不同的光子碰撞,贡献不同,如何量化?
- Radiant energy:
h和c是常数,只有\(\lambda\)要关注,它也代表了颜色
-
Radiant flux:
\[\Phi = \lim\limits_{\Delta \to 0} \dfrac{\Delta Q}{\Delta t}=\dfrac{dQ}{dt} \] -
Irradiance:
The average flux
\[\dfrac{\Phi}{A} \]\[E(p)=\lim\limits_{\Delta\to0}\dfrac{\Delta\Phi(p)}{\Delta A}=\dfrac{d\Phi(p)}{dA} \]
如何量化颜色
描述irradiance per unit wavelength
单位时间单位面积单位波长的能量
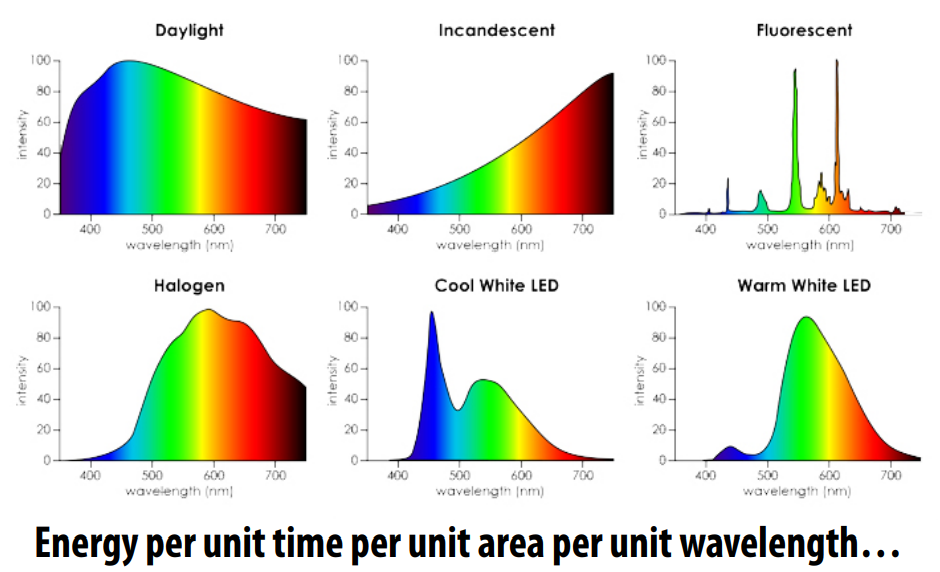
Lambert's Law
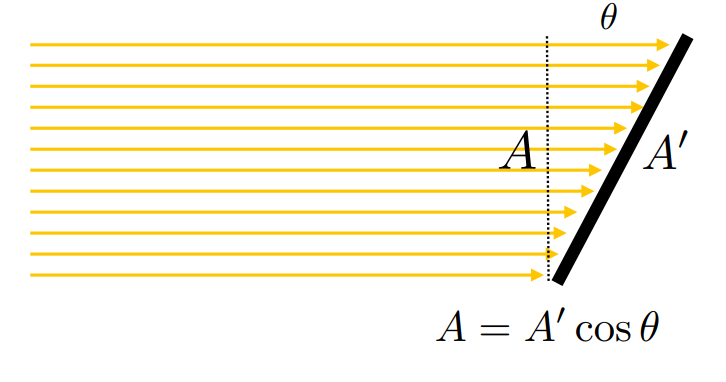
斜着照,用正交投影面积
简单光照
单位光线向量和平面单位法向量内积,即为光强

(通常)把光源放到无穷远,得到平行光
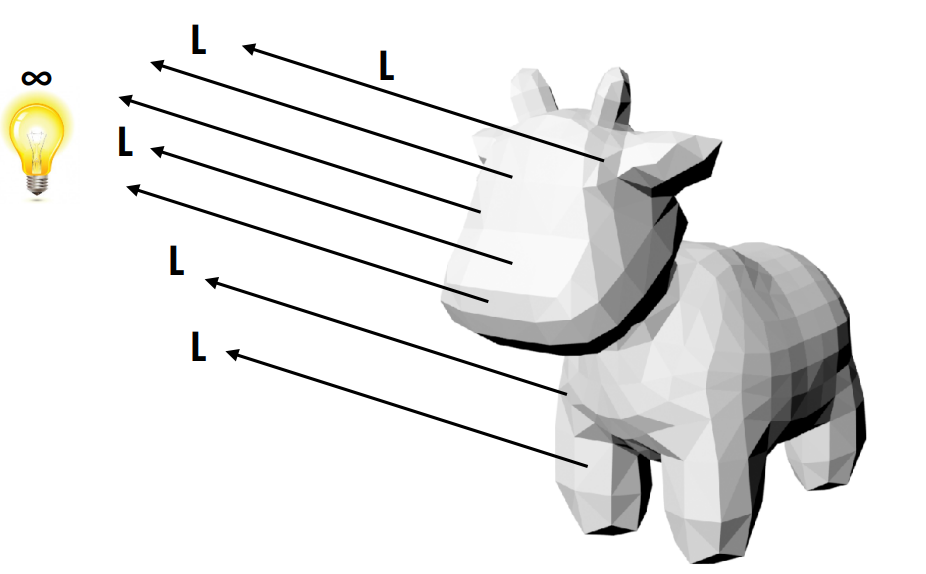
对于点光源,其irradiance与平方成反比(类似高斯定理?)
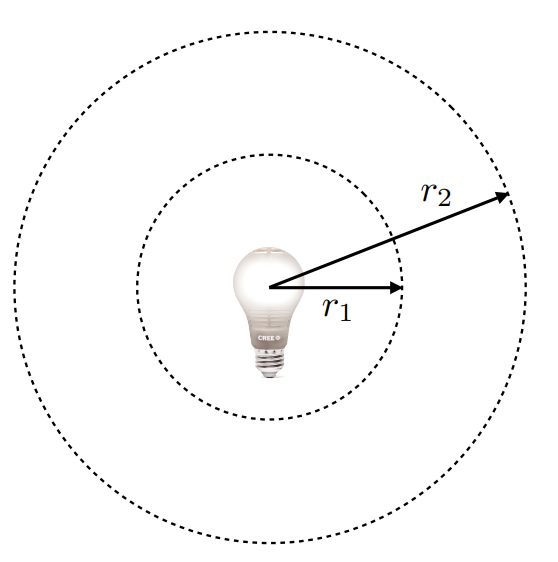
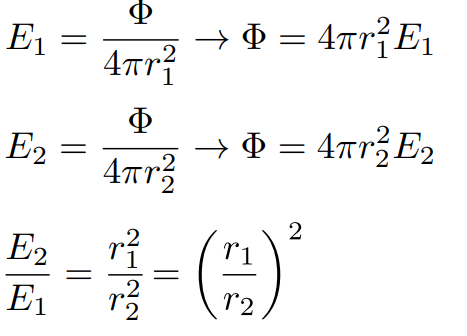
立体弧度
一个圆有\(2\pi\)个弧度
弧度\(\theta = \dfrac{L}{r}\)
一个球有\(4\pi\)个弧度
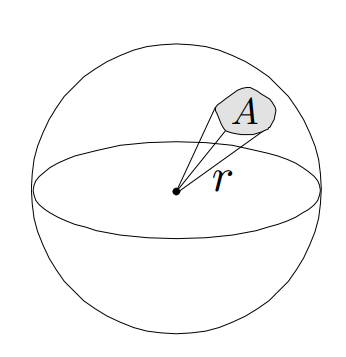
立体弧度\(\Omega = \dfrac{A}{r^2}\)
Radiance是irradiance的立体弧度密度
定义
辐射场是一个五维函数
左边的\(\mathbb R^3\)是三维空间,\(S^2\)是球坐标下的视角
右边的\(\mathbb R^3\)是线性RGB空间
所以,辐射场是这样的一个五维函数:
亦可以写成向量形式
\(\mathbf x\)是位置向量,\(\mathbf \omega\)是视角的单位向量
也就是说,Radiance是一条沿着方向\(\omega\)的光线通过点\(p\)的能量
*渲染方程
一点\(\mathbf x\)的辐射\(L_0\)由两部分组成,一部分是自己发出的\(L_e\)(emit),另一部分是该点折射在方向\(\mathbf d\)上的辐射
其中\(\Omega\)为入射方向\(\omega_i\)的半球集,\(f_r\)为散射函数,\(L_i\)为\(\omega_i\)方向的辐射,\(\theta\)为\(\omega_i\)和\(\mathbf d\)的夹角