二叉搜索树02--[前序/中序/后序/层次遍历&&接口设计]

1.二叉树的遍历

1.1前序遍历

递归遍历

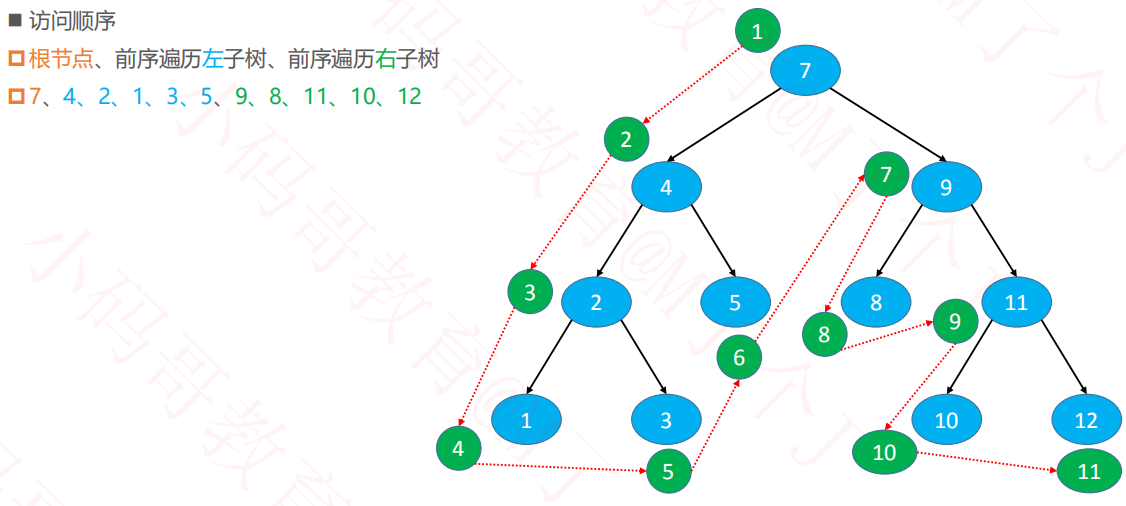
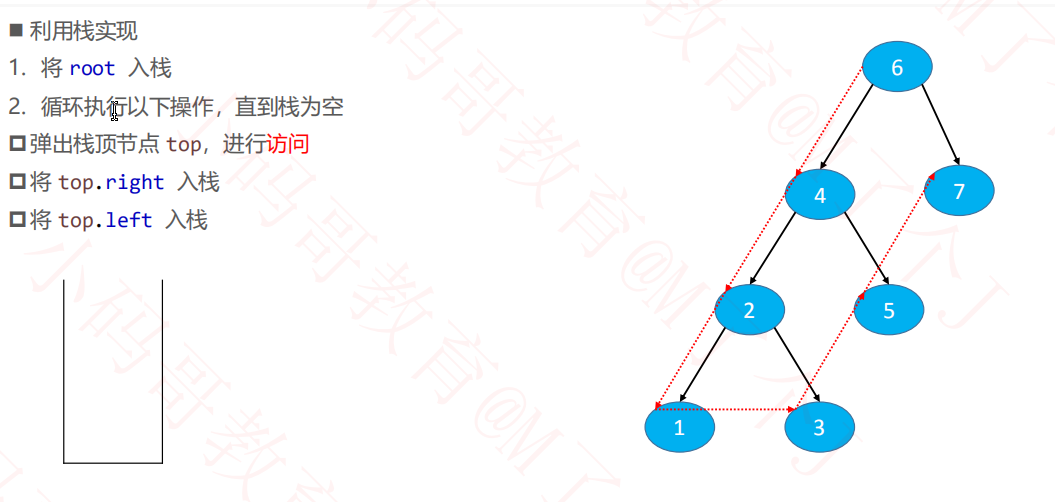
前序非递归遍历

 

  

代码-递归版本

    /**
     * 前序遍历
     */
    public void preorderTraversal() {
        preorderTraversal(root);
    }
    
    private void preorderTraversal(Node<E> node) {
        if (node == null) return;
        
        System.out.println(node.element);
        preorderTraversal(node.left);
        preorderTraversal(node.right);
    }

1.3中序遍历

递归遍历

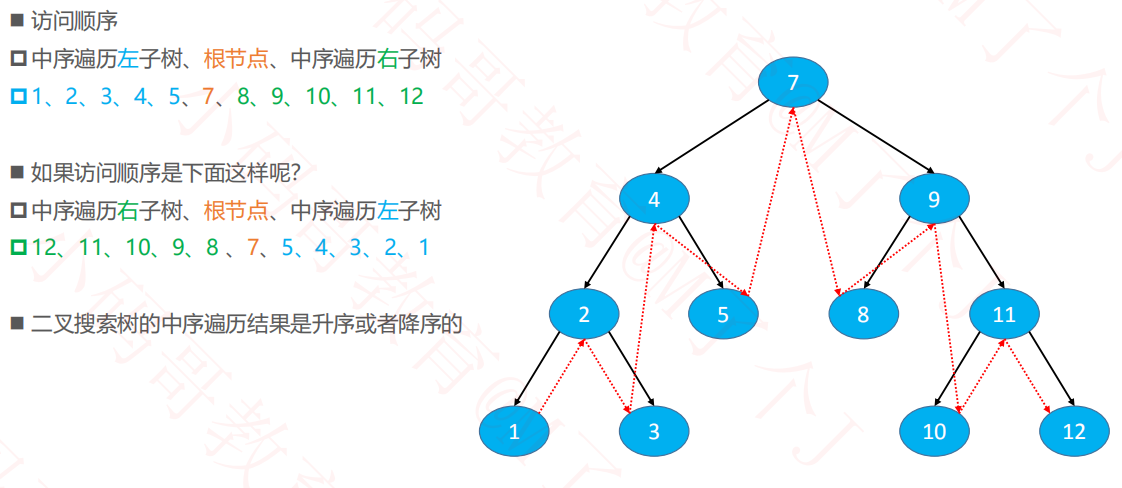
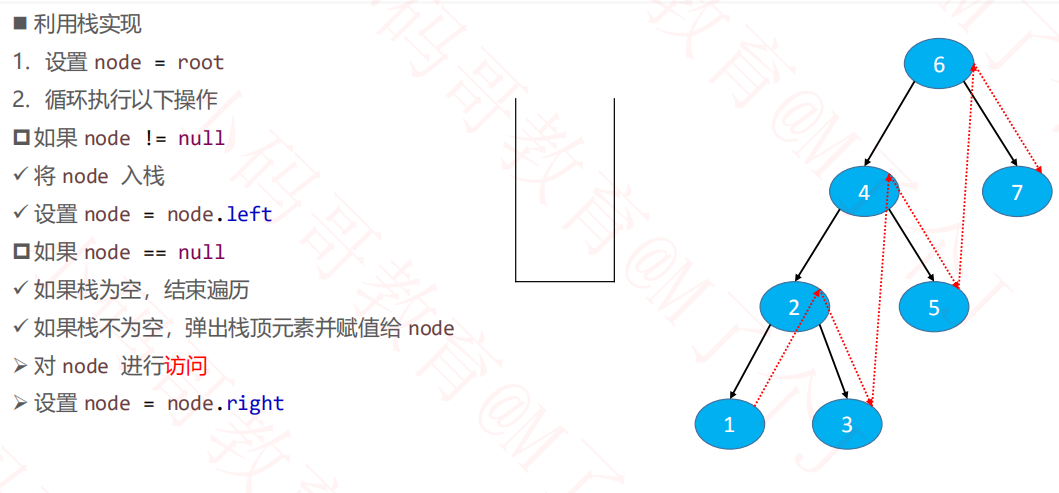
 非递归遍历

 

 代码--递归版本

    /**
     * 中序遍历
     */
    public void inorderTraversal() {
        inorderTraversal(root);
    }
    
    private void inorderTraversal(Node<E> node) {
        if (node == null) return;
        
        inorderTraversal(node.left);
        System.out.println(node.element);
        inorderTraversal(node.right);
    }

 1.4后序遍历

递归遍历

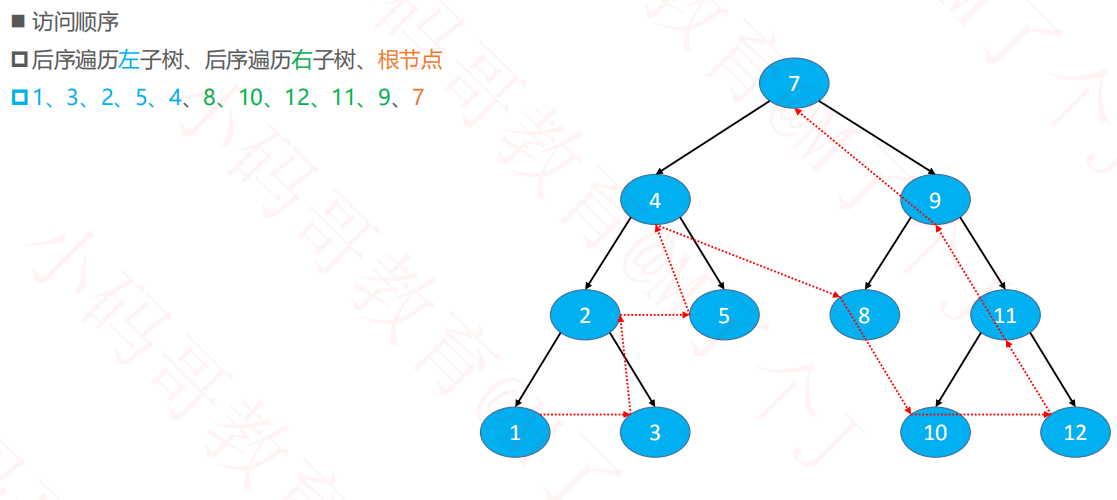
 非递归遍历

 

代码--递归版本

    /**
     * 后序遍历
     */
    public void postorderTraversal() {
        postorderTraversal(root);
    }
    
    private void postorderTraversal(Node<E> node) {
        if (node == null) return;

        postorderTraversal(node.left);
        postorderTraversal(node.right);
        System.out.println(node.element);
    }

1.5层次遍历

递归版本

 

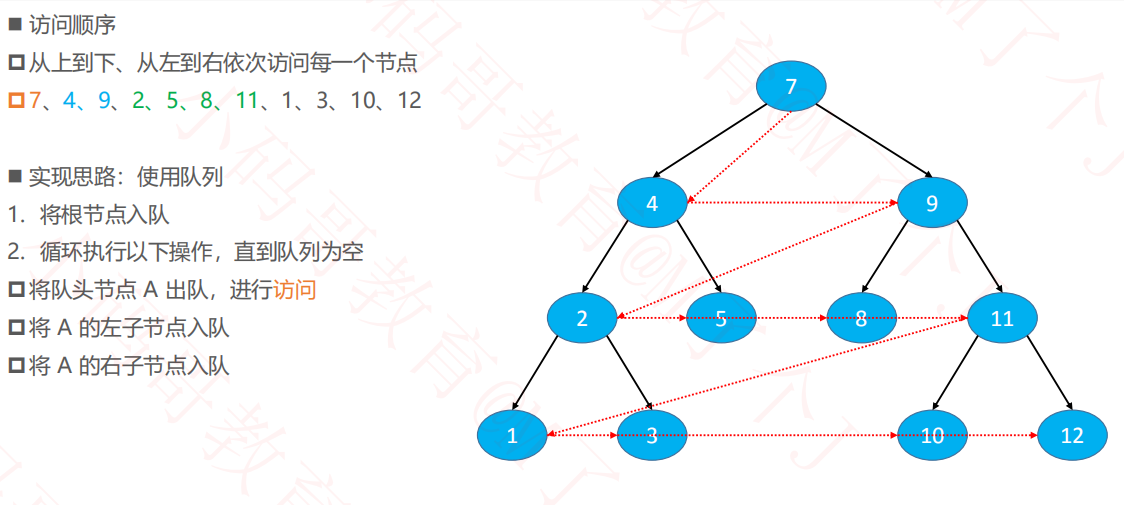
 代码--递归版本

    /**
     * 层序遍历
     */
    public void levelOrderTraversal() {
        if (root == null) return;
        
        Queue<Node<E>> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            Node<E> node = queue.poll();
            System.out.println(node.element);
            
            if (node.left != null) {
                queue.offer(node.left);
            }
            
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

2.遍历接口设计

2.1控制遍历元素的输出设计

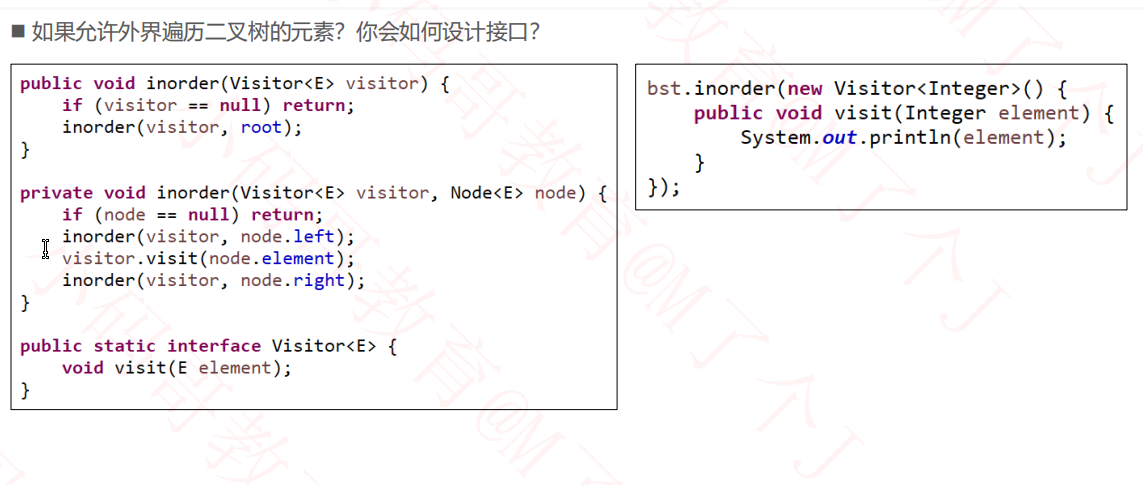
代码

BinarySearchTree.java

public static interface  Visitor<E> {
        
         void  visit(E element);
    }    
public void inorder(Visitor<E> visitor) {
        if (visitor == null) return;
        inorder(root, visitor);
    }
    
    private void inorder(Node<E> node, Visitor<E> visitor) {
        //这是递归终止
        if (node == null || visitor.stop) return;
        
        inorder(node.left, visitor);
        //这是打印终止
        if (visitor.stop) return;
        visitor.stop = visitor.visit(node.element);
        inorder(node.right, visitor);
    }

main.java

bst.inorder(new Visitor<Integer>() {
        public void visit(Integer element) {
            System.out.print(element );
        }
    });

2.2增强遍历接口--控制遍历的个数 在什么时候进行停止操作

 

代码

BinarySearchTree.java

    public static abstract class Visitor<E> {
        boolean stop;
        /**
         * @return 如果返回true，就代表停止遍历
         */
        public abstract boolean visit(E element);
    }
        
    public void inorder(Visitor<E> visitor) {
        if (visitor == null) return;
        inorder(root, visitor);
    }
    
    private void inorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) return;
        
        inorder(node.left, visitor);
        if (visitor.stop) return;
        visitor.stop = visitor.visit(node.element);
        inorder(node.right, visitor);
    }

main.java

bst.inorder(new Visitor<Integer>() {
            public boolean visit(Integer element) {
                System.out.print(element + " ");
                return element == 4 ? true : false;
            }
        });

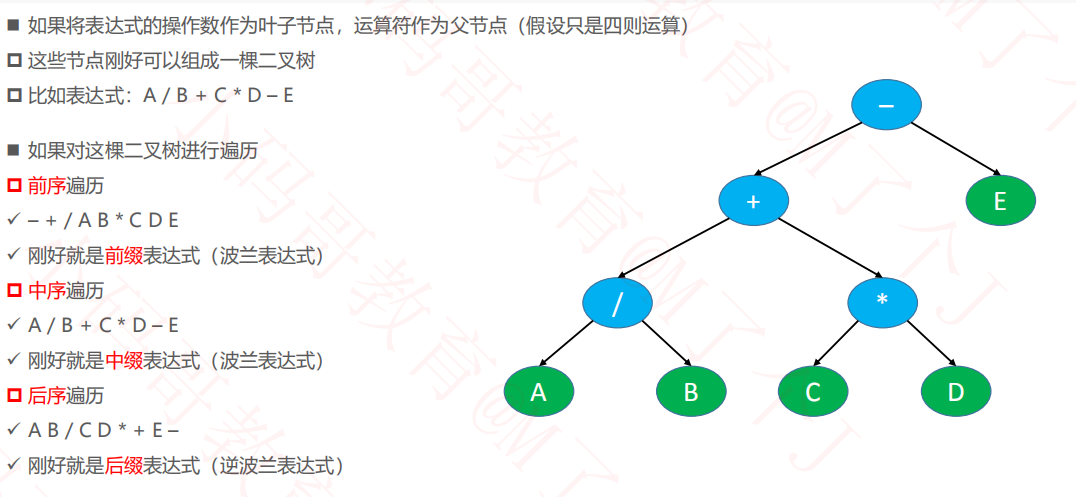
3.遍历的应用