二叉搜索树01--[简介&&接口设计&&比较器&&打印器]

1.何为二叉搜索树

 

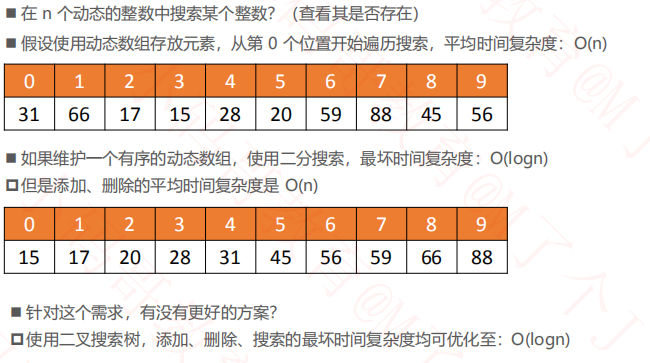
1.1二叉搜索树的接口设计

我们节点在哪一层和添加的顺序无关所以 BST不需要索引

 

1.2添加节点

 

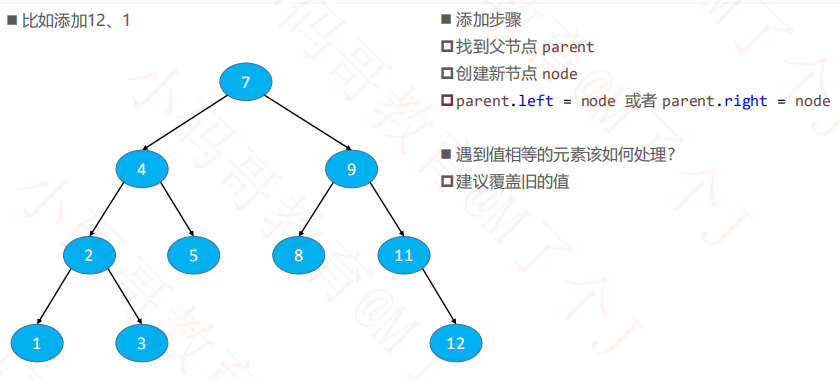
1.3元素比较方案

通过创建比较器接口实现自定义比较规则 即使是相同对象

相关代码

 1.4可视化网站推荐

http://520it.com/binarytrees/

http://btv.melezinek.cz/binary-search-tree.html

https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

https://yangez.github.io/btree-js/

https://www.codelike.in/

 1.5打印二叉树

使用注意事项

效果图

 

打印器代码

file包

package com.mj.file;

import java.io.BufferedWriter;
import java.io.File;
import java.io.FileWriter;

public class Files {
    
    public static void writeToFile(String filePath, Object data) {
        writeToFile(filePath, data, false);
    }
    
    public static void writeToFile(String filePath, Object data, boolean append) {
        if (filePath == null || data == null) return;
        
        try {
            File file = new File(filePath);
            if (!file.exists()) {
                file.getParentFile().mkdirs();
                file.createNewFile();
            }
            
            try (FileWriter writer = new FileWriter(file, append);
                    BufferedWriter out = new BufferedWriter(writer) ) {
                out.write(data.toString());
                out.flush();
            }
        } catch (Exception e) {
            e.printStackTrace();
        }
    }
    
}

1.6相关代码

1.BinarySearchTree类

package com.mj;

import java.util.Comparator;
import java.util.LinkedList;
import java.util.Queue;

import com.mj.printer.BinaryTreeInfo;

@SuppressWarnings("unchecked")
public class BinarySearchTree<E> implements BinaryTreeInfo {
    private int size;
    private Node<E> root;
    private Comparator<E> comparator;
    
    public BinarySearchTree() {
        this(null);
    }
    
    public BinarySearchTree(Comparator<E> comparator) {
        this.comparator = comparator;
    }
    
    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public void clear() {
        root = null;
        size = 0;
    }

    public void add(E element) {
        elementNotNullCheck(element);
        
        // 添加第一个节点
        if (root == null) {
            root = new Node<>(element, null);
            size++;
            return;
        }
        
        // 添加的不是第一个节点
        // 找到父节点
        Node<E> parent = root;
        Node<E> node = root;
        int cmp = 0;
        do {
            cmp = compare(element, node.element);
            parent = node;
            if (cmp > 0) {
                node = node.right;
            } else if (cmp < 0) {
                node = node.left;
            } else { // 相等
                node.element = element;
                return;
            }
        } while (node != null);

        // 看看插入到父节点的哪个位置
        Node<E> newNode = new Node<>(element, parent);
        if (cmp > 0) {
            parent.right = newNode;
        } else {
            parent.left = newNode;
        }
        size++;
    }

    public void remove(E element) {
        remove(node(element));
    }

    public boolean contains(E element) {
        return node(element) != null;
    }
    
    private void remove(Node<E> node) {
        if (node == null) return;
        
        size--;
        
        if (node.hasTwoChildren()) { // 度为2的节点
            // 找到后继节点
            Node<E> s = successor(node);
            // 用后继节点的值覆盖度为2的节点的值
            node.element = s.element;
            // 删除后继节点
            node = s;
        }
        
        // 删除node节点（node的度必然是1或者0）
        Node<E> replacement = node.left != null ? node.left : node.right;
        
        if (replacement != null) { // node是度为1的节点
            // 更改parent
            replacement.parent = node.parent;
            // 更改parent的left、right的指向
            if (node.parent == null) { // node是度为1的节点并且是根节点
                root = replacement;
            } else if (node == node.parent.left) {
                node.parent.left = replacement;
            } else { // node == node.parent.right
                node.parent.right = replacement;
            }
        } else if (node.parent == null) { // node是叶子节点并且是根节点
            root = null;
        } else { // node是叶子节点，但不是根节点
            if (node == node.parent.left) {
                node.parent.left = null;
            } else { // node == node.parent.right
                node.parent.right = null;
            }
        }
    }
    
    private Node<E> node(E element) {
        Node<E> node = root;
        while (node != null) {
            int cmp = compare(element, node.element);
            if (cmp == 0) return node;
            if (cmp > 0) {
                node = node.right;
            } else { // cmp < 0
                node = node.left;
            }
        }
        return null;
    }
    
//    /**
//     * 前序遍历
//     */
//    public void preorderTraversal() {
//        preorderTraversal(root);
//    }
//    
//    private void preorderTraversal(Node<E> node) {
//        if (node == null) return;
//        
//        System.out.println(node.element);
//        preorderTraversal(node.left);
//        preorderTraversal(node.right);
//    }
//    
//    /**
//     * 中序遍历
//     */
//    public void inorderTraversal() {
//        inorderTraversal(root);
//    }
//    
//    private void inorderTraversal(Node<E> node) {
//        if (node == null) return;
//        
//        inorderTraversal(node.left);
//        System.out.println(node.element);
//        inorderTraversal(node.right);
//    }
//    
//    /**
//     * 后序遍历
//     */
//    public void postorderTraversal() {
//        postorderTraversal(root);
//    }
//    
//    private void postorderTraversal(Node<E> node) {
//        if (node == null) return;
//
//        postorderTraversal(node.left);
//        postorderTraversal(node.right);
//        System.out.println(node.element);
//    }
//    
//    /**
//     * 层序遍历
//     */
//    public void levelOrderTraversal() {
//        if (root == null) return;
//        
//        Queue<Node<E>> queue = new LinkedList<>();
//        queue.offer(root);
//        
//        while (!queue.isEmpty()) {
//            Node<E> node = queue.poll();
//            System.out.println(node.element);
//            
//            if (node.left != null) {
//                queue.offer(node.left);
//            }
//            
//            if (node.right != null) {
//                queue.offer(node.right);
//            }
//        }
//    }
    
    public void preorder(Visitor<E> visitor) {
        if (visitor == null) return;
        preorder(root, visitor);
    }
    
    private void preorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) return;
        
        visitor.stop = visitor.visit(node.element);
        preorder(node.left, visitor);
        preorder(node.right, visitor);
    }
    
    public void inorder(Visitor<E> visitor) {
        if (visitor == null) return;
        inorder(root, visitor);
    }
    
    private void inorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) return;
        
        inorder(node.left, visitor);
        if (visitor.stop) return;
        visitor.stop = visitor.visit(node.element);
        inorder(node.right, visitor);
    }
    
    public void postorder(Visitor<E> visitor) {
        if (visitor == null) return;
        postorder(root, visitor);
    }
    
    private void postorder(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) return;
        
        postorder(node.left, visitor);
        postorder(node.right, visitor);
        if (visitor.stop) return;
        visitor.stop = visitor.visit(node.element);
    }
    
    public void levelOrder(Visitor<E> visitor) {
        if (root == null || visitor == null) return;
        
        Queue<Node<E>> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            Node<E> node = queue.poll();
            if (visitor.visit(node.element)) return;
            
            if (node.left != null) {
                queue.offer(node.left);
            }
            
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
    
    public boolean isComplete() {
        if (root == null) return false;
        
        Queue<Node<E>> queue = new LinkedList<>();
        queue.offer(root);

        boolean leaf = false;
        while (!queue.isEmpty()) {
            Node<E> node = queue.poll();
            if (leaf && !node.isLeaf()) return false;
            
            if (node.left != null) {
                queue.offer(node.left);
            } else if (node.right != null) { // node.left == null && node.right != null
                return false;
            }
            
            if (node.right != null) {
                queue.offer(node.right);
            } else { // node.right == null
                leaf = true;
            }
        }
        
        return true;
    }
    
//    public boolean isComplete() {
//        if (root == null) return false;
//        
//        Queue<Node<E>> queue = new LinkedList<>();
//        queue.offer(root);
//        
//        boolean leaf = false;
//        while (!queue.isEmpty()) {
//            Node<E> node = queue.poll();
//            if (leaf && !node.isLeaf()) return false;
//
//            if (node.left != null && node.right != null) {
//                queue.offer(node.left);
//                queue.offer(node.right);
//            } else if (node.left == null && node.right != null) {
//                return false;
//            } else { // 后面遍历的节点都必须是叶子节点
//                leaf = true;
//                if (node.left != null) {
//                    queue.offer(node.left);
//                }
//            }
//        }
//        
//        return true;
//    }
    
    public int height() {
        if (root == null) return 0;
        
        // 树的高度
        int height = 0;
        // 存储着每一层的元素数量
        int levelSize = 1;
        Queue<Node<E>> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            Node<E> node = queue.poll();
            levelSize--;
            
            if (node.left != null) {
                queue.offer(node.left);
            }
            
            if (node.right != null) {
                queue.offer(node.right);
            }

            if (levelSize == 0) { // 意味着即将要访问下一层
                levelSize = queue.size();
                height++;
            }
        }
        
        return height;
    }
    
    public int height2() {
        return height(root);
    }
    
    private int height(Node<E> node) {
        if (node == null) return 0;
        return 1 + Math.max(height(node.left), height(node.right));
    }
    
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        toString(root, sb, "");
        return sb.toString();
    }
    
    private void toString(Node<E> node, StringBuilder sb, String prefix) {
        if (node == null) return;

        toString(node.left, sb, prefix + "L---");
        sb.append(prefix).append(node.element).append("
");
        toString(node.right, sb, prefix + "R---");
    }
    
    /**
     * @return 返回值等于0，代表e1和e2相等；返回值大于0，代表e1大于e2；返回值小于于0，代表e1小于e2
     */
    private int compare(E e1, E e2) {
        if (comparator != null) {
            return comparator.compare(e1, e2);
        }
        return ((Comparable<E>)e1).compareTo(e2);
    }
    
    private void elementNotNullCheck(E element) {
        if (element == null) {
            throw new IllegalArgumentException("element must not be null");
        }
    }
    
    @SuppressWarnings("unused")
    private Node<E> predecessor(Node<E> node) {
        if (node == null) return null;
        
        // 前驱节点在左子树当中（left.right.right.right....）
        Node<E> p = node.left;
        if (p != null) {
            while (p.right != null) {
                p = p.right;
            }
            return p;
        }
        
        // 从父节点、祖父节点中寻找前驱节点
        while (node.parent != null && node == node.parent.left) {
            node = node.parent;
        }

        // node.parent == null
        // node == node.parent.right
        return node.parent;
    }
    
    private Node<E> successor(Node<E> node) {
        if (node == null) return null;
        
        // 前驱节点在左子树当中（right.left.left.left....）
        Node<E> p = node.right;
        if (p != null) {
            while (p.left != null) {
                p = p.left;
            }
            return p;
        }
        
        // 从父节点、祖父节点中寻找前驱节点
        while (node.parent != null && node == node.parent.right) {
            node = node.parent;
        }

        return node.parent;
    }
    
    public static abstract class Visitor<E> {
        boolean stop;
        /**
         * @return 如果返回true，就代表停止遍历
         */
        public abstract boolean visit(E element);
    }

    private static class Node<E> {
        E element;
        Node<E> left;
        Node<E> right;
        Node<E> parent;
        public Node(E element, Node<E> parent) {
            this.element = element;
            this.parent = parent;
        }
        
        public boolean isLeaf() {
            return left == null && right == null;
        }
        
        public boolean hasTwoChildren() {
            return left != null && right != null;
        }
    }

    @Override
    public Object root() {
        return root;
    }

    @Override
    public Object left(Object node) {
        return ((Node<E>)node).left;
    }

    @Override
    public Object right(Object node) {
        return ((Node<E>)node).right;
    }

    @Override
    public Object string(Object node) {
        Node<E> myNode = (Node<E>)node;
        String parentString = "null";
        if (myNode.parent != null) {
            parentString = myNode.parent.element.toString();
        }
        return myNode.element + "_p(" + parentString + ")";
    }
}

2.main函数

package com.mj;

import java.util.Comparator;

import com.mj.BinarySearchTree.Visitor;
import com.mj.file.Files;
import com.mj.printer.BinaryTreeInfo;
import com.mj.printer.BinaryTrees;

@SuppressWarnings("unused")
public class Main {
    
    private static class PersonComparator implements Comparator<Person> {
        public int compare(Person e1, Person e2) {
            return e1.getAge() - e2.getAge();
        }
    }
    
    private static class PersonComparator2 implements Comparator<Person> {
        public int compare(Person e1, Person e2) {
            return e2.getAge() - e1.getAge();
        }
    }

    static void test1() {
        Integer data[] = new Integer[] {
                7, 4, 9, 2, 5, 8, 11, 3, 12, 1
        };
        
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        
        BinaryTrees.println(bst);
    }
    
    static void test2() {
        Integer data[] = new Integer[] {
                7, 4, 9, 2, 5, 8, 11, 3, 12, 1
        };
        
        BinarySearchTree<Person> bst1 = new BinarySearchTree<>();
        for (int i = 0; i < data.length; i++) {
            bst1.add(new Person(data[i]));
        }
        
        BinaryTrees.println(bst1);
        
        BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new Comparator<Person>() {
            public int compare(Person o1, Person o2) {
                return o2.getAge() - o1.getAge();
            }
        });
        for (int i = 0; i < data.length; i++) {
            bst2.add(new Person(data[i]));
        }
        BinaryTrees.println(bst2);
    }
    
    static void test3() {
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        for (int i = 0; i < 40; i++) {
            bst.add((int)(Math.random() * 100));
        }
        
        String str = BinaryTrees.printString(bst);
        str += "
";
        Files.writeToFile("F:/1.txt", str, true);
        
        // BinaryTrees.println(bst);
    }
    
    static void test4() {
        BinaryTrees.println(new BinaryTreeInfo() {
            
            @Override
            public Object string(Object node) {
                return node.toString() + "_";
            }
            
            @Override
            public Object root() {
                return "A";
            }
            
            @Override
            public Object right(Object node) {
                if (node.equals("A")) return "C";
                if (node.equals("C")) return "E";
                return null;
            }
            
            @Override
            public Object left(Object node) {
                if (node.equals("A")) return "B";
                if (node.equals("C")) return "D";
                return null;
            }
        });
        
        // test3();
        
        
        /*
         * Java的匿名类，类似于iOS中的Block、JS中的闭包（function）
         */
        
//        BinarySearchTree<Person> bst1 = new BinarySearchTree<>(new Comparator<Person>() {
//            @Override
//            public int compare(Person o1, Person o2) {
//                return 0;
//            }
//        });
//        bst1.add(new Person(12));
//        bst1.add(new Person(15));
//        
//        BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new PersonComparator());
//        bst2.add(new Person(12));
//        bst2.add(new Person(15));
//
        
        
//        BinarySearchTree<Car> bst4 = new BinarySearchTree<>(new Car);
//        
//        
//        java.util.Comparator<Integer> iComparator;
    }
    
    static void test5() {
        BinarySearchTree<Person> bst = new BinarySearchTree<>();
        bst.add(new Person(10, "jack"));
        bst.add(new Person(12, "rose"));
        bst.add(new Person(6, "jim"));
        
        bst.add(new Person(10, "michael"));
        
        BinaryTrees.println(bst);
    }
    
    static void test6() {
        Integer data[] = new Integer[] {
                7, 4, 9, 2, 5
        };
        
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        
//        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
//        for (int i = 0; i < 10; i++) {
//            bst.add((int)(Math.random() * 100));
//        }
        BinaryTrees.println(bst);
        System.out.println(bst.isComplete());
        
        // bst.levelOrderTraversal();
        
        /*
         *       7
         *    4    9
            2   5
         */
        
//        bst.levelOrder(new Visitor<Integer>() {
//            public void visit(Integer element) {
//                System.out.print("_" + element + "_ ");
//            }
//        });
        
//        bst.inorder(new Visitor<Integer>() {
//            public void visit(Integer element) {
//                System.out.print("_" + (element + 3) + "_ ");
//            }
//        });
        
        // System.out.println(bst.height());
    }
    
    static void test7() {
        Integer data[] = new Integer[] {
                7, 4, 9, 2, 5, 8, 11, 3, 12, 1
        };
        
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        
        BinaryTrees.println(bst);
        
        bst.remove(7);
        
        BinaryTrees.println(bst);
    }
    
    static void test8() {
        Integer data[] = new Integer[] {
                7, 4, 9, 2, 1
        };
        
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        BinaryTrees.println(bst);
        System.out.println(bst.isComplete());
    }
    
    static void test9() {
        Integer data[] = new Integer[] {
                7, 4, 9, 2, 1
        };
        
        BinarySearchTree<Integer> bst = new BinarySearchTree<>();
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        BinaryTrees.println(bst);
        
        bst.preorder(new Visitor<Integer>() {
            public boolean visit(Integer element) {
                System.out.print(element + " ");
                return element == 2 ? true : false;
            }
        });
        System.out.println();
        
        bst.inorder(new Visitor<Integer>() {
            public boolean visit(Integer element) {
                System.out.print(element + " ");
                return element == 4 ? true : false;
            }
        });
        System.out.println();
        
        bst.postorder(new Visitor<Integer>() {
            public boolean visit(Integer element) {
                System.out.print(element + " ");
                return element == 4 ? true : false;
            }
        });
        System.out.println();
        
        bst.levelOrder(new Visitor<Integer>() {
            public boolean visit(Integer element) {
                System.out.print(element + " ");
                return element == 9 ? true : false;
            }
        });
        System.out.println();
    }
    
    public static void main(String[] args) {
        test9();
    }
}

3.Person类

package com.mj;

public class Person implements Comparable<Person> {
    private int age;
    private String name;
    
    public int getAge() {
        return age;
    }

    public void setAge(int age) {
        this.age = age;
    }

    public Person(int age) {
        this.age = age;
    }

    public Person(int age, String name) {
        this.age = age;
        this.name = name;
    }

    @Override
    public int compareTo(Person e) {
//        if (age > e.age) return 1;
//        if (age < e.age) return -1;
//        return 0;
        return age - e.age;
    }
    
    @Override
    public String toString() {
        return age + "_" + name;
    }
    
}