特征工程(Feature Engineering)目的是最大限度地从原始数据中提取特征以供算法和模型使用,是数据挖掘模型开发中最耗时、最重要的一步。内容包括:特征处理(Feature Processing)、特征选择(Feature Selection)。
本部分系统的总结特征工作的一些基本概念,以及自己在模型开发中所总结的一些方法。并结合具体案例(iris数据集)配合sklearn数据包梳理整个特征工程的操作流程。
目录:
5 实践
在介绍特征工程之前,我们先看两张图。
图一是基本的数据挖掘场景,该图清晰的解释了数据挖掘的整体流程
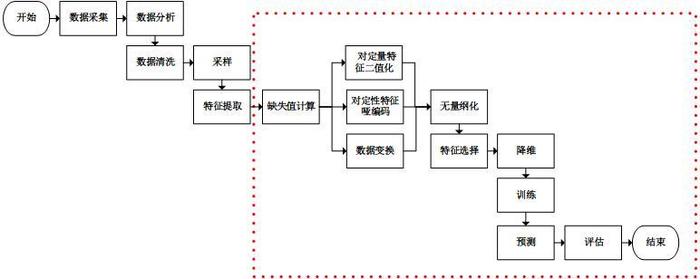
图二总结了特征工程的常见方法和步骤
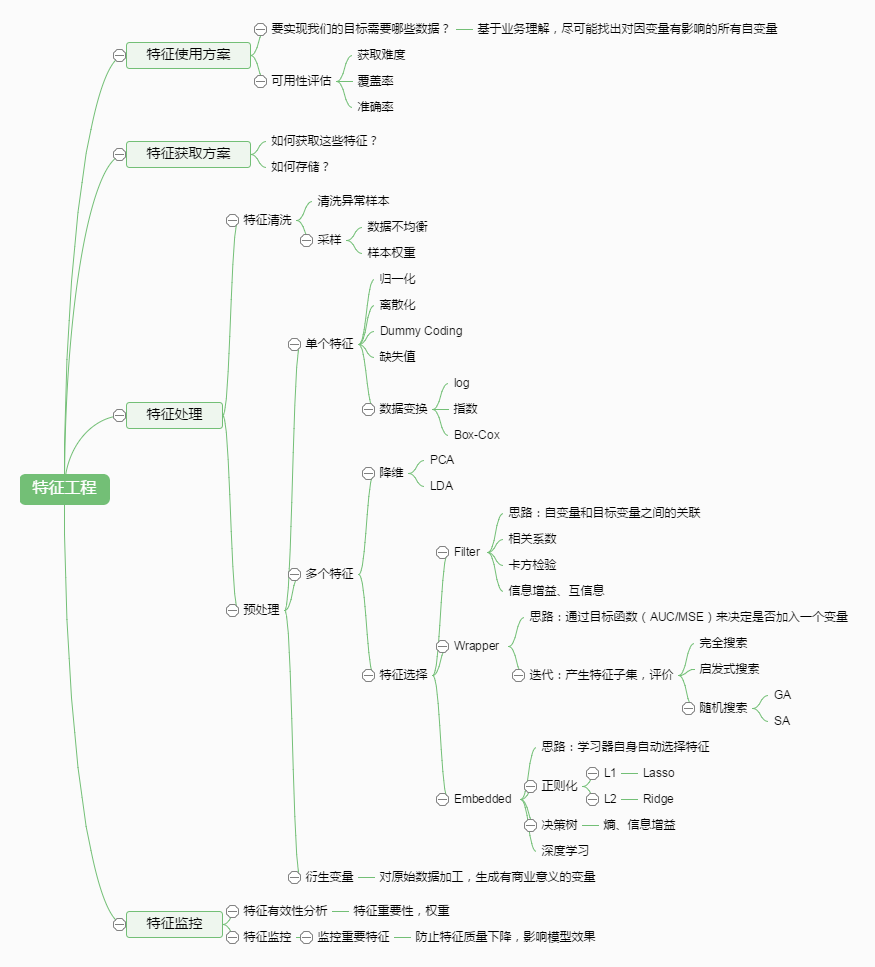
一、特征处理(Feature Processing)
特征也就是我们常常说的变量/自变量,一般分为三类:
· 连续型
· 无序类别(离散)型
· 有序类别(离散)型
1.1 连续型特征
- 不处理
除了归一化(去中心,方差归一),不用做太多特殊处理,可以直接把连续特征扔到模型里使用。根据模型类型而定。
- 离散化
对于一些特殊的模型(信用评分卡)开发,有时候我们需要对连续型的特征(年龄、收入)进行离散化。
离散化方法的关键是怎么确定分段中的离散点,下面介绍几种常用的离散化方法:
· 等距离离散(等距分组) 顾名思义,就是离散点选取等距点。
· 等样本点离散(等深分组) 选取的离散点保证落在每段里的样本点数量大致相同
· 决策树离散化(最优分组) 决策树离散化方法通常也是每次离散化一个连续特征,原理如下: 单独用此特征和目标值y训练一个决策树模型,然后把训练获得的模型内的特征分割点作为离散化的离散点。
· 其他离散化方法 其中,最优分组除决策树方法以外,还可以使用卡方分箱的方法,这种方法在评分卡开发中比较常见。
- 函数转换
有时我们的模型的假设条件是要求自变量或因变量服从某特殊分布(如正态分布),或者说自变量或因变量服从该分布时,模型的表现较好。这个时候我们就需要对特征或因变量进行非线性函数转换。这个方法操作起来很简单,但记得对新加入的特征做归一化。对于特征的转换,需要将转换之后的特征和原特征一起加入训练模型进行训练。
1.2 无序类别(离散)型
- 数值化
· one-hot编码 一个变量k个值就转换成k个虚拟变量,优点:简单,且保证无共线性,缺点:太稀(稀疏矩阵)。
避免产生稀疏矩阵的常见方法是降维,将变量值较多的分类维度,尽可能降到最少,能降则降,不能降的,别勉强。
此外,在实际应用中,通过梯度下降法求解的模型一般都是需要归一化的,比如线性回归、logistic回归、KNN、SVM、神经网络等模型。但树形模型不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、随机森林(Random Forest)。
1.3 有序类别(离散)型
· label encoder 一个变量的k个值,按序转换成k个数字(1,2,3…k)。例如一个人的状态status有三种取值:bad, normal, good,显然bad < normal < good。这个时候bad, normal, good就可以分别转换成 1、2、3。但该方法局限性较大不推荐
· 生成哑变量 与one-hot编码一样,都是将一个变量的k个值生成k个哑变量,但注意不能丢了变量值之间的顺序关系。一般的表达方式如下:
|
status取值
|
向量表示
|
|
bad
|
(1, 0, 0)
|
|
normal
|
(1, 1, 0)
|
|
good
|
(1, 1, 1)
|
二、特征选择(Feature Selection)
也被称为variable selection或者attribute selection. 是选取已有属性的子集subset来进行建模的一种方式。
特征选择一般有两个目的:
· 剔除对因变量影响较小或无任何相关性的自变量,使得模型预测或分类效果达到理想值。
· 提高模型的可解释性
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
· 特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
· 特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。除方差法外,本文介绍的其他方法均从相关性考虑。
根据特征选择的形式又可以将特征选择方法分为3种:
· Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
· Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
· Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
参考: