本系列为吴恩达斯坦福CS229机器学习课程笔记整理,以下为笔记目录:
(一)线性回归
(二)逻辑回归
(三)神经网络
(四)算法分析与优化
(五)支持向量机
(六)K-Means
(七)特征降维
(八)异常检测
(九)推荐系统
(十)大规模机器学习
第二章 逻辑回归
使用线性回归来处理 0/1 分类问题比较困难,因此引入逻辑回归来完成 0/1 分类问题,逻辑一词也代表了是(1)和非(0)。
一、Sigmoid预测函数
在逻辑回归中,定义预测函数为: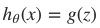
g(z) 称之为 Sigmoid Function,亦称 Logic Function
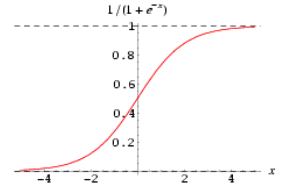
二、决策边界
决策边界是预测函数 hθ(x) 的属性,而不是训练集属性。这是因为能作出“划清”类间界限的只有 hθ(x) ,而训练集只是用来训练和调节参数的。
- 线性决策边界
- 非线性决策边界

二、预测代价函数
对于分类任务来说,我们就是要反复调节参数 θ ,亦即反复转动决策边界来作出更精确的预测。假定我们有代价函数 J(θ) ,其用来评估某个 θ 值时的预测精度,当找到代价函数的最小值时,就能作出最准确的预测。
通常,代价函数具备越少的极小值,就越容易找到其最小值,也就越容易达到最准确的预测。 -> 局部最小和全局最小
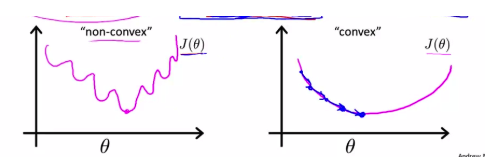
逻辑回归定义的代价函数为:
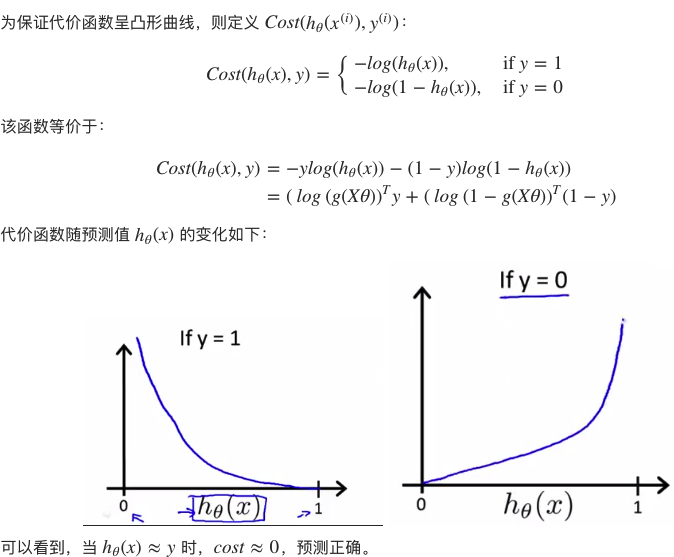
三、最小化代价函数
同样采用BGD和SGD两种方式

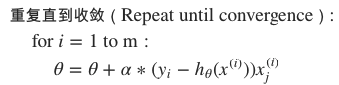
四、正则化
解决过拟合问题:
1)减少特征数
2)平滑曲线
弱化高阶项系数(减弱曲线曲折度),称为对参数 θ 的惩罚(penalize)。——正则化
· 线性回归中正则化:

其中,参数 λ 主要是完成以下两个任务:
- 保证对数据的拟合良好
- 保证 θ 足够小,避免过拟合问题。(λ 越大,要使 J(θ) 变小,惩罚力度就要变大,这样 θ 会被惩罚得越惨(越小),即要避免过拟合,我们显然应当增大 λ 的值。)
· 逻辑回归中的正则化
五、多分类问题
通常采用 One-vs-All,亦称 One-vs-the Rest 方法来实现多分类,其将多分类问题转化为了多次二分类问题。
假定完成 K 个分类,One-vs-All 的执行过程如下:
- 轮流选中某一类型 i ,将其视为正样本,即 “1” 分类,剩下样本都看做是负样本,即 “0” 分类。
- 训练逻辑回归模型得到参数 θ(1),θ(2),...,θ(K) ,即总共获得了 K−1 个决策边界。
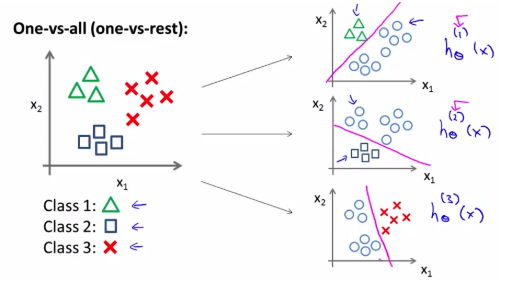
给定输入 x,为确定其分类,需要分别计算 h(k)θ(x),k=1,...,K ,h(k)θ(x) 越趋近于1,x 越接近是第k类:
