Dus on tree
树上并查集?。 啊这,并不是的啦,他利用了树上启发式合并的思想。
他主要解决不带修改且主要询问子树信息的树上问题。
先来看到例题,CF600E 。
这不就是树上莫队的经典题吗?。 会莫队的大佬一眼就秒了。
不会的蒟蒻我只能打打暴力,骗骗分。
首先,我们暴力其实很好打,就是对每个点都统计一下他子树的答案,时间复杂度为 O((n^2)).
这显然,我们是不能接受的,我们需要优化。
Dus on tree 利用轻重链剖分的思想,把他的复杂度优化为 O((n log n)) 的。
我们递归处理子树的时候,重复计算了很多种状态,我们就要考虑剪枝,减去重复的状态。
实际上,我们最后处理的子树肯定是不需要删除他的贡献的,在计算他的父亲 (x) 的答案的时候,直接利用他的信息,
就可以直接推出他父亲的答案。
我们就要确定一种顺序,使我们遍历子树节点的数目尽可能少。
我们选的最后遍历的要为他的重儿子(重儿子子树中的节点是最多的)
就这样 Dus on tree 的算法流程就是:
-
递归处理每个轻儿子,同时消除轻儿子的影响。
-
递归重儿子,不消除重儿子的影响。
-
统计轻儿子对答案的贡献。
-
将轻儿子和重儿子的信息合并,得出这个节点的答案。
-
消除轻儿子对答案的影响
大致的代码张这样:
void dfs(int x,int fa,int opt)
{
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa || to == son[x]) continue;
dfs(to,1);//递归轻儿子
}
if(son[x]) dfs(son[x],0);//帝国重儿子
add(x);//统计轻儿子对答案的贡献
ans[x] = now_ans;//合并轻儿子和重儿子得出这个点的答案
if(opt == 1) delet(x);//如果他是轻儿子,消除他的影响
}
图例长这样
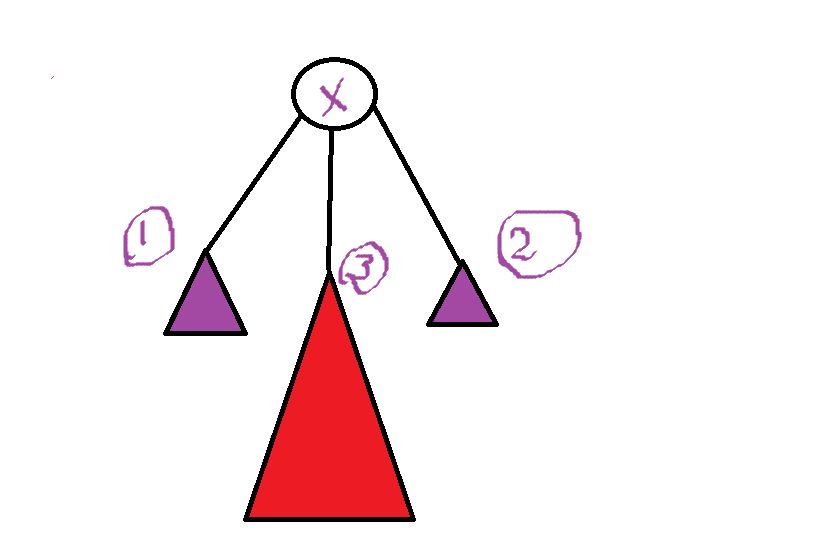
紫色的是他的轻儿子,红色的是他的重儿子,序号是他的遍历顺序。
这不是和普通的爆搜没什么区别吗?为什么复杂度不是O((n^2))
下面,我们简单证明一下他的复杂度,不愿意看的可以直接跳过。
性质:一个节点到根的路径上轻边个数不会超过 logn 条
证明:设根到该节点有 (x) 的轻边,该节点的大小为 (y),根据轻重边的定义,轻边所连向的点的大小不会成为该节点
总大小的一般。这样每经过一条轻边,(y) 的上限就会 /2,所以 (x) < (log n)
然而这条性质并不能解决问题,我们考虑一个点会被访问多少次
一个点被访问到,只有两种情况
1、在暴力统计轻边的时候访问到。根据前面的性质,该次数 < (log n)
2、通过重边 在遍历的时候被访问到,显然只有一次
如果统计一个点的贡献的复杂度为O(1)的话,该算法的复杂度为O((nlog n))
我们上面的例题就可以直接套板子了。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N = 1e5+10;
int n,m,tot,u,v,max_c,now_ans,heavy_son;
int siz[N],fa[N],son[N],head[N],cnt[N],c[N],ans[N];
struct node
{
int to,net;
}e[N<<1];
void add_(int x,int y)
{
e[++tot].to = y;
e[tot].net = head[x];
head[x] = tot;
}
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s =s * 10+ch - '0'; ch = getchar();}
return s * w;
}
void get_tree(int x)
{
siz[x] = 1;
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa[x]) continue;
fa[to] = x;
get_tree(to);
siz[x] += siz[to];
if(siz[son[x]] < siz[to]) son[x] = to;
}
}
void add(int x,int val)
{
cnt[c[x]] += val;
// printf("----------->
");
// cout<<max_c<<" "<<now_ans<<endl;
if(cnt[c[x]] > max_c)//max_c 记录当前出现次数最多的颜色的出现次数
{
max_c = cnt[c[x]];
now_ans = c[x];
}
else if(cnt[c[x]] == max_c)//相等的话,记录一下编号和
{
now_ans += c[x];
}
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa[x] || to == heavy_son) continue;
add(to,val);
}
}
void dfs(int x,int type)
{
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
if(to == fa[x] || to == son[x]) continue;
dfs(to,1);
}
if(son[x])
{
dfs(son[x],0);
heavy_son = son[x];
}
add(x,1);
ans[x] = now_ans;
heavy_son = 0;
if(type == 1)
{
add(x,-1);
max_c = now_ans = 0;
}
}
signed main()
{
n = read();
for(int i = 1; i <= n; i++) c[i] = read();
for(int i = 1; i <= n-1; i++)
{
u = read(); v = read();
add_(u,v); add_(v,u);
}
get_tree(1); dfs(1,0);
for(int i = 1; i <= n; i++) printf("%lld ",ans[i]);
return 0;
}
一个需要注意的点是 不能记录出现次数最多的颜色编号,而应该记录这个颜色出现的次数。(我在这里卡了好几回)
因为你这样会重复计算,第二组样例就是一组 很好的 Hack 数据。