题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
5 5 2 24 7 3 7 8 0 1 2 1 5 3 1 4 1 3 4 2 3 2 2 4 5 1 5 1 3 2 1 3
2 21
说明
时空限制:1s,128M
数据规模:
对于30%的数据: N leq 10, M leq 10N≤10,M≤10
对于70%的数据: N leq {10}^3, M leq {10}^3N≤103,M≤103
对于100%的数据: N leq {10}^5, M leq {10}^5N≤105,M≤105
( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:
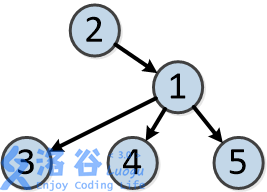
各个操作如下:
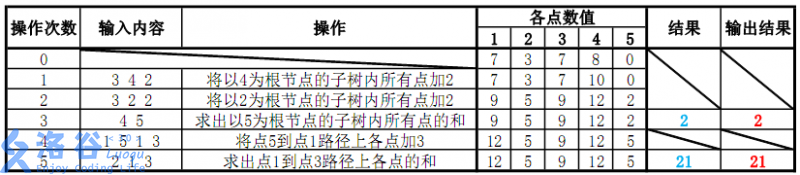
故输出应依次为2、21(重要的事情说三遍:记得取模)
【思路分析】
这道题说是树链剖分模板,其实还要套一个线段树就OK了
我们发现,这个树链剖分与求LCA的唯一区别在于需要维护链上树上的信息,那么我们怎么实现维护链上树上的信息呢?
这里我们就要好好利用我们剖分树链时的遍历顺序!!!
对于求链上的信息时,因为我们第二次dfs优先遍历的是父节点的最大子节点,也就是先遍历重链,所以我们每条重链上的遍历的编号是连续的,所以我们可以用线段树维护这段区间的信息。
对于求子树的信息时,因为我们每次是先遍历完了一个父节点的所有子节点后在遍历另一个父节点,导致我们每棵子树也都是编号连续的,同理也可以用线段树维护。
1 int ask1(int v,int lx,int rx) 2 { 3 pushdown(v); 4 if(t[v].l==lx&&t[v].r==rx) 5 return t[v].key; 6 int ls=t[v].son[0],rs=t[v].son[1],mid=(t[v].l+t[v].r)/2; 7 if(lx>mid) return ask1(rs,lx,rx); 8 else 9 if(rx<=mid) return ask1(ls,lx,rx); 10 else 11 return (ask1(ls,lx,mid)+ask1(rs,mid+1,rx))%mod; 12 } 13 int tree_sum(int x,int y) 14 { 15 int ans=0; 16 while(top[x]!=top[y]) 17 { 18 if(dep[top[x]]<dep[top[y]]) {int t=x;x=y;y=t;} 19 ans=(ans+ask1(1,idx[top[x]],idx[x]))%mod; 20 x=fa[top[x]]; 21 } 22 if(dep[x]>dep[y]) {int t=x;x=y;y=t;} 23 ans=(ans+ask1(1,idx[x],idx[y]))%mod; 24 return ans; 25 }
那么对于链上、子树修改也同理,每次去当前点到链顶进行维护
【代码实现】
1 #include<cstdio> 2 #include<vector> 3 using namespace std; 4 const int maxn=100000; 5 int top[maxn+5],fa[maxn+5],son[maxn+5],siz[maxn+5],dep[maxn+5],head[maxn+5],ww[maxn+5],ord[maxn+5],idx[maxn+5]; 6 struct sd{ 7 int to,next; 8 }edge[2*maxn+5]; 9 struct sd2{ 10 int l,r,son[2],key,add; 11 }t[maxn*2+5]; 12 int cnt,n,m,root,mod; 13 void add_edge(int a,int b) 14 { 15 edge[++cnt].to=b; 16 edge[cnt].next=head[a]; 17 head[a]=cnt; 18 } 19 int dfs(int now,int ff,int deep) 20 { 21 fa[now]=ff,dep[now]=deep,siz[now]=1; 22 int ms=-1,maxx=-1; 23 for(int i=head[now];i!=0;i=edge[i].next) 24 { 25 if(edge[i].to!=ff) 26 { 27 int gg=dfs(edge[i].to,now,deep+1); 28 if(maxx<gg) 29 { maxx=gg,ms=edge[i].to; } 30 siz[now]+=gg; 31 } 32 } 33 if(ms==-1) son[now]=now; 34 else son[now]=ms; 35 return siz[now]; 36 } 37 void dfs2(int now,int tt) 38 { 39 cnt++,ord[cnt]=now,idx[now]=cnt,top[now]=tt; 40 if(son[now]==now) return; 41 dfs2(son[now],tt); 42 for(int i=head[now];i!=0;i=edge[i].next) 43 { 44 if(edge[i].to!=fa[now]&&edge[i].to!=son[now]) 45 dfs2(edge[i].to,edge[i].to); 46 } 47 } 48 void build(int &v,int lx,int rx) 49 { 50 cnt++,v=cnt,t[v].l=lx,t[v].r=rx; 51 if(lx==rx) 52 { t[v].key=ww[ord[lx]];return; } 53 int mid=(lx+rx)/2; 54 build(t[v].son[0],lx,mid); 55 build(t[v].son[1],mid+1,rx); 56 t[v].key=t[t[v].son[0]].key+t[t[v].son[1]].key; 57 } 58 void pushdown(int v) 59 { 60 if(t[v].l==t[v].r) return; 61 if(t[v].add) 62 { 63 int ls=t[v].son[0],rs=t[v].son[1]; 64 t[ls].key=(t[ls].key+(t[ls].r-t[ls].l+1)*t[v].add)%mod; 65 t[rs].key=(t[rs].key+(t[rs].r-t[rs].l+1)*t[v].add)%mod; 66 t[ls].add=(t[ls].add+t[v].add)%mod,t[rs].add=(t[rs].add+t[v].add)%mod; 67 t[v].add=0; 68 } 69 } 70 void add1(int v,int lx,int rx,int z) 71 { 72 pushdown(v); 73 if(t[v].l==lx&&t[v].r==rx) 74 { 75 t[v].add=(t[v].add+z)%mod; 76 t[v].key=(z*(t[v].r-t[v].l+1)+t[v].key)%mod; 77 return; 78 } 79 int ls=t[v].son[0],rs=t[v].son[1],mid=(t[v].l+t[v].r)/2; 80 if(lx>mid) add1(rs,lx,rx,z); 81 else 82 if(rx<=mid) add1(ls,lx,rx,z); 83 else 84 { 85 add1(ls,lx,mid,z); 86 add1(rs,mid+1,rx,z); 87 } 88 t[v].key=(t[ls].key+t[rs].key)%mod; 89 } 90 int ask1(int v,int lx,int rx) 91 { 92 pushdown(v); 93 if(t[v].l==lx&&t[v].r==rx) 94 return t[v].key; 95 int ls=t[v].son[0],rs=t[v].son[1],mid=(t[v].l+t[v].r)/2; 96 if(lx>mid) return ask1(rs,lx,rx); 97 else 98 if(rx<=mid) return ask1(ls,lx,rx); 99 else 100 return (ask1(ls,lx,mid)+ask1(rs,mid+1,rx))%mod; 101 } 102 void tree_add(int x,int y,int z) 103 { 104 while(top[x]!=top[y]) 105 { 106 if(dep[top[x]]<dep[top[y]]) {int t=x;x=y;y=t;} 107 add1(1,idx[top[x]],idx[x],z); 108 x=fa[top[x]]; 109 } 110 if(dep[x]>dep[y]) {int t=x;x=y;y=t;} 111 add1(1,idx[x],idx[y],z); 112 } 113 int tree_sum(int x,int y) 114 { 115 int ans=0; 116 while(top[x]!=top[y]) 117 { 118 if(dep[top[x]]<dep[top[y]]) {int t=x;x=y;y=t;} 119 ans=(ans+ask1(1,idx[top[x]],idx[x]))%mod; 120 x=fa[top[x]]; 121 } 122 if(dep[x]>dep[y]) {int t=x;x=y;y=t;} 123 ans=(ans+ask1(1,idx[x],idx[y]))%mod; 124 return ans; 125 } 126 int main() 127 { 128 scanf("%d%d%d%d",&n,&m,&root,&mod); 129 for(int i=1;i<=n;i++) scanf("%d",&ww[i]); 130 for(int i=1;i<n;i++) 131 { 132 int a,b; 133 scanf("%d%d",&a,&b); 134 add_edge(a,b);add_edge(b,a); 135 } 136 dfs(root,0,1); 137 cnt=0; 138 dfs2(root,root); 139 int rr;cnt=0; 140 build(rr,1,n); 141 for(int i=1;i<=m;i++) 142 { 143 int orz; 144 scanf("%d",&orz); 145 if(orz==1) 146 { 147 int x,y,z; 148 scanf("%d%d%d",&x,&y,&z); 149 tree_add(x,y,z); 150 } 151 if(orz==2) 152 { 153 int x,y; 154 scanf("%d%d",&x,&y); 155 printf("%d ",tree_sum(x,y)); 156 } 157 if(orz==3) 158 { 159 int x,z; 160 scanf("%d%d",&x,&z); 161 add1(1,idx[x],idx[x]+siz[x]-1,z); 162 } 163 if(orz==4) 164 { 165 int x; 166 scanf("%d",&x); 167 printf("%d ",ask1(1,idx[x],idx[x]+siz[x]-1)); 168 } 169 } 170 return 0; 171 }