【学习】可持久化线段树（主席树）

可持久化数据结构是为了保存这个数据结构的所有历史版本

---

正文

这是一棵非常好看的线段树

考虑一个问题，现在修改6号节点，同时保留原始信息，怎么做

重构一棵线段树，该修改的就修改，其余信息复制

显然不对因为我们在说可持久化而不是重构

遵从不浪费原则，我们要尽可能多的利用不需要修改的节点

根据线段树的知识，我们知道修改一个点的同时也会影响他的父亲及祖先

所以标星的点是要被修改的

我们把要修改的点重建，保留不需要修改的就变成了介个样子

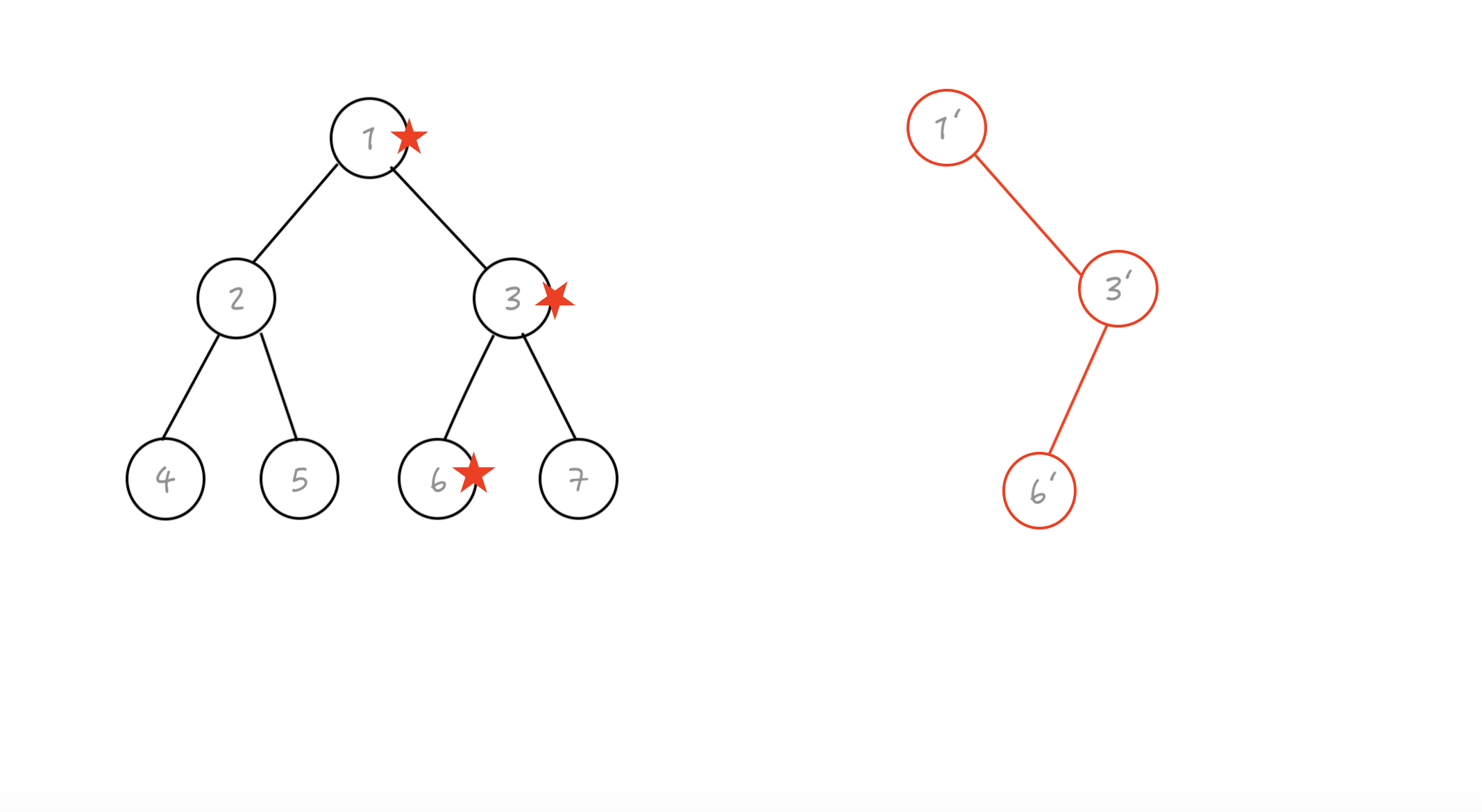
同时我们还要充分利用旧的线段树，那怎么办呢

直接把他指过去就行了

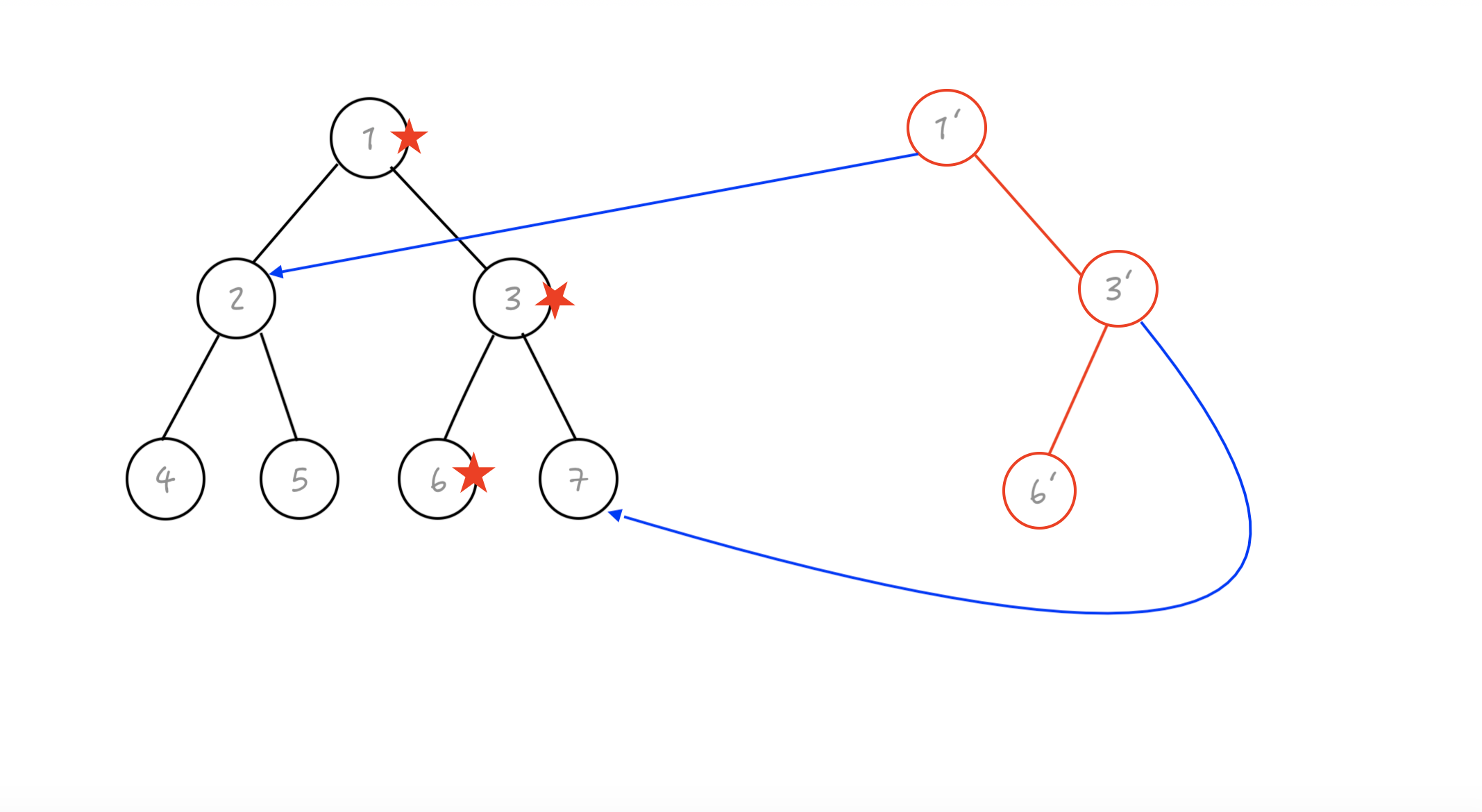
由于1的左子树和3的右儿子是全部不用修改，所以直接指过去是可以维护的

---

（不带修）静态查询区间第k大(小)

//
//  main.cpp
//  【模版】可持久化线段树（主席树）
//
//  Created by gengyf on 2019/7/12.
//  Copyright © 2019 yifan Geng. All rights reserved.
//

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#define mid (l+r)/2
using namespace std;
const int N = 200010;
int n, q, m, cnt = 0;
int a[N], b[N], T[N];
int sum[N<<5], L[N<<5], R[N<<5];
inline int build(int l, int r){
    int rt = ++ cnt;
    sum[rt] = 0;
    if (l < r){
        L[rt] = build(l, mid);
        R[rt] = build(mid+1, r);
    }
    return rt;
}
inline int update(int pre, int l, int r, int x){
    int rt = ++ cnt;
    L[rt] = L[pre]; R[rt] = R[pre]; sum[rt] = sum[pre]+1;
    if (l < r){
        if (x <= mid) L[rt] = update(L[pre], l, mid, x);
        else R[rt] = update(R[pre], mid+1, r, x);
    }
    return rt;
}
inline int query(int u, int v, int l, int r, int k){
    if (l >= r) return l;
    int x = sum[L[v]] - sum[L[u]];
    if (x >= k) return query(L[u], L[v], l, mid, k);
    else return query(R[u], R[v], mid+1, r, k-x);
}
int main(){
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; i ++){
        scanf("%d", &a[i]);
        b[i] = a[i];
    }
    sort(b+1, b+1+n);
    m = unique(b+1, b+1+n)-b-1;
    T[0] = build(1, m);
    for (int i = 1; i <= n; i ++){
        int t = lower_bound(b+1, b+1+m, a[i])-b;
        T[i] = update(T[i-1], 1, m, t);
    }
    while (q --){
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        int t = query(T[x-1], T[y], 1, m, z);
        printf("%d
", b[t]);
    }
    return 0;
}

（带修）动态区间第k大（小）洛谷P2617

//
//  main.cpp
//  【模版】动态区间第k大(树状数组主席树)
//
//  Created by gengyf on 2019/9/1.
//  Copyright © 2019 yifan Geng. All rights reserved.
//

#include <iostream>
using namespace std;
namespace gengyf{
    const int N=5e5+1;
    struct ls{
        int w,num;
    }pp[N<<1];//离散化
    struct que{
        char ss[3];
        int l,r,k;
    }q[N];//询问
    struct tree{
        int w,l,r;
    }t[N<<5];
    inline bool cmp(ls x,ls y){
        return x.w<y.w;
    }
    int root[N];
    int pas[N],now[N],L,R;
    int e,ran,sz,a[N<<1],s[N];//离散化数组大小,排名个数,排名数组,原值数组
    inline void lisan(){//离散化
        sort(pp+1,pp+e+1,cmp);
        a[pp[1].num]=ran=1;
        s[1]=pp[1].w;
        for(int i=2;i<=e;i++){
            if(pp[i].w!=pp[i-1].w){
                s[++ran]=pp[i].w;
            }
            a[pp[i].num]=ran;
        }
    }
    inline int lowbit(int x){
        return x&-x;
    }
    inline void add(int &now,int l,int r,int x){//新建
        if(!now){
            now=++sz;
        }
        t[now].w++;
        if(l==r){
            return ;
        }
        int mid=(l+r)>>1;
        if(x<=mid)add(t[now].l,l,mid,x);
        else add(t[now].r,mid+1,r,x);
    }
    inline void del(int now,int l,int r,int x){//删除
        t[now].w--;
        if(l==r){
            return ;
        }
        int mid=(l+r)>>1;
        if(x<=mid){
            del(t[now].l,l,mid,x);
            return ;
        }
        del(t[now].r,mid+1,r,x);
    }
    inline int kth(int l,int r,int k){//查询
        if(l==r){
            return l;
        }
        int sum=0;
        for(int i=1;i<=L;i++){
            sum-=t[t[pas[i]].l].w;
        }
        for(int i=1;i<=R;i++){
            sum+=t[t[now[i]].l].w;
        }
        int mid=(l+r)>>1;
        if(sum>=k){
            for(int i=1;i<=L;i++){
                pas[i]=t[pas[i]].l;
            }
            for(int i=1;i<=R;i++){
                now[i]=t[now[i]].l;
            }
            return kth(l,mid,k);
        }
        for(int i=1;i<=L;i++){
            pas[i]=t[pas[i]].r;
        }
        for(int i=1;i<=R;i++){
            now[i]=t[now[i]].r;
        }
        return kth(mid+1,r,k-sum);
    }
    int n,m;
    int main(){
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++){
            scanf("%d",&pp[i].w);
            pp[i].num=i;
        }
        e=n;
        for(int i=1;i<=m;i++){
            scanf("%s%d%d",&q[i].ss,&q[i].l,&q[i].r);
            if(q[i].ss[0]=='Q'){
                scanf("%d",&q[i].k);
            }
            else {
                e++;
                pp[e].w=q[i].r;pp[e].num=n+i;
            }
        }
        lisan();
        for(int i=1;i<=n;i++){
            int x=i;
            while(x<=n){
                add(root[x],1,ran,a[i]);
                x+=lowbit(x);
            }
        }
        for(int i=1;i<=m;i++){
            if(q[i].ss[0]=='Q'){
                L=R=0;
                int Now=q[i].l-1;
                while(Now){
                    pas[++L]=root[Now];
                    Now-=lowbit(Now);
                }
                Now=q[i].r;
                while(Now){
                    now[++R]=root[Now];
                    Now-=lowbit(Now);
                }
                printf("%d
",s[kth(1,ran,q[i].k)]);
            }
            else {
                int Now=q[i].l;
                while(Now<=n){
                    del(root[Now],1,ran,a[q[i].l]);
                    Now+=lowbit(Now);
                }
                Now=q[i].l;
                while(Now<=n){
                    add(root[Now],1,ran,a[i+n]);
                    Now+=lowbit(Now);
                }
                a[q[i].l]=a[i+n];
                continue;
            }
        }
        return 0;
    }
}
int main() {
    gengyf::main();
    return 0;
}

ps：目前只放了代码，会补解释的QwQ（咕咕咕～