马尔科可模型
马尔可夫模型是由Andrei A. Markov于1913年提出的
$\bullet$ 设 $S $是一个由有限个状态组成的集合
$S=\{1, 2, 3, …,n-1, n\}$
随机序列 $X $ 在 $ t $时刻所处的状态为 $ q_t$,其中 $q_t \in S$,若有:
\[ P(q_t=j |q_{t-1}=i, q_{t-2}=k,\cdots)=P(q_t=j |q_{t-1}= i) \]
\[{a_{ij}} \ge 0\;\;\;\sum\limits_j^n {{a_{ij}} = 1} \]
则随机序列 $X $构成一个一阶马尔科夫链。(Markov Chain)
$\bullet$ 令 $ P(q_t=j|q_{t-1}=i)=P(q_s=j|q_{s-1}=i)$(说明是齐次的,即转移概率不随时间改变),则对于所有的 $i,j$有下面的关系成立:
\[{a_{ij}} = P({q_t} = j|{q_{t - 1}} = i)\;1 \le i,j \le n\]
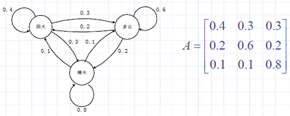
$\bullet$ 一阶马尔科夫模型可以描述为一个二元组 $(S,A)\;\;S$是状态的集合,而$A$是所有状态转移概率组成的一个 $n$行 $n$列的矩阵,其中每一个元素 $a_{ij}$为从状态i转移到状态 $j$ 的概率。
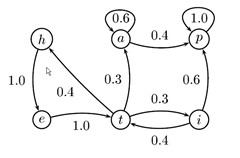
$\bullet$ 同有限状态自动机类似,状态转移关系也可以用状态转换图来表示。
马尔科可模型举例
$\bullet$ 天气的变化,三种状态{1(阴天), 2(多云), 3(晴天)}
$\bullet$ 今天的天气情况仅和昨天的天气状况有关
$\bullet$ 根据对历史数据的观察得到下列状态转移关系
$\bullet$ 对于马尔科夫模型,给定了观察序列,同时也就确定了状态转换序列。例如有关天气状况的观察序列
(晴 晴 晴 阴 阴 晴 云 晴)
则状态转换序列为
(3, 3, 3, 1, 1, 3, 2, 3 )
$\bullet$ 如果把晴天称为状态3的输出,阴天称为状态1的输出,多云称为状态2的输出。根据观察到的输出序列就可以决定模型中的状态转换序列。(状态和输出是一对一的关系)
坛子与小球
$\bullet$ 在一个房间中,假定有 $N$个坛子,每个坛子中都装有不同颜色的小球,并且假定总共有 $M$种不同颜色的小球
$\bullet$ 一个精灵在房间中首先随机地选择一个坛子,再从这个坛子中随机选择一个小球,并把小球的颜色报告给房间外面的人员记录下来作为观察值
$\bullet$ 精灵然后把球放回到坛子中,以当前的坛子为条件再随机选择一个坛子,从中随机选择一个小球,并报告小球的颜色,然后放回小球,如此继续…,随着时间的推移,房间外的人会得到由这个过程产生的一个小球颜色的序列
$\bullet$ 如果令每一个坛子对应与一个状态,可以用一个一阶马尔科夫过程来描述坛子的选择过程
$\bullet$ 在马尔科夫过程中,每个状态只有一个输出,但在坛子和小球的问题中。可以从每个坛子中拿出不同颜色的小球。也就是每个状态能按照特定的概率分布产生多个输出
$\bullet$ 在坛子与小球问题中,如果给定一个观察序列(不同颜色的小球序列),不能直接确定状态转换序列(坛子的序列),因为状态转移过程被隐藏起来了。所以这类随机过程被称为隐马尔科夫过程
隐马尔可夫模型
$\bullet$ 隐马尔可夫模型 $\lambda$可以表示为一个五元组 $(S, V, A, B, \pi)$
$S$ 是一组状态的集合
$S={1, 2, 3, …, N }$ (状态 $n$对应坛子 $n$)
$V$是一组输出符号组成的集合(取Visible之意?)
$V={v_1, v_2, v_3, \cdots, v_M}$ ($v_1$对应红色小球)
$A$是状态转移矩阵,$N$行 $N$列
$A=[a_{ij}], a_{ij}=P(q_{t+1}=j|q_t=i),1\le i, j\le N$
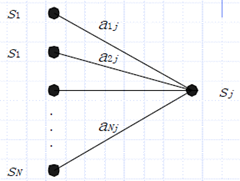
$B$是输出符号的概率分布
$B= {b_j(k)} b_j(k)$ 表示在状态 $j$时输出符号 $v_k$的概率
$b_j(k)= P(v_k|j), 1\le k\le M ,1\le j\le N$
$\pi$是初始状态概率分布 $\pi=\{\pi_i\}$
$\pi_i= P(q_1= i)$表示时刻1选择某个状态的概率
$\bullet$ 隐马尔可夫过程是一个双重随机过程,其中一重随机过程不能直接观察到,通过状态转移概率矩阵描述。另一重随机过程输出可以观察到的观察符号,这由输出概率来定义
利用隐马尔可夫模型生成观察序列
$\bullet$ 可以把隐马尔可夫模型看做符号序列的生成装置,按照一定的步骤,隐马尔可夫模型可以生成下面的符号序列:
$O=(o_1,o_2,\cdots,o_T)$
$\1.$ 令 $t=1$,按照初始状态概率分布 $\pi $选择一个初始状态 $ q_1=i $
$\2.$ 按照状态i输出符号的概率分布 $ b_i(k) $选择一个输出值 $ o_t=v_k $
$\3.$ 按照状态转移概率分布 $ a_{ij} $选择一个后继状态 $ q_{t+1}=j $
$\4.$ 若 $ t<T $,令 $ t=t+1 $,并且转移到算法第2步继续执行,否则结束
抛掷硬币
$\bullet$ 三枚硬币,随机选择一枚,进行抛掷,记录抛掷结果。可以描述为一个三个状态的隐马尔科夫模型 $\lambda$
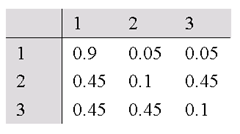
$\lambda = (S, V, A, B, \pi) $,其中 $ S = \{1, 2, 3\} V = \{H,T\} $
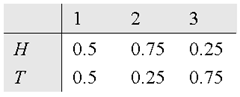
$A$ 如下表所示 $B$ 如下表所示
$ \pi = \{1/3, 1/3, 1/3\}$
$\bullet$ 问题一:
给定上述模型,观察到下列抛掷结果的概率是多少?
$O = (H H H H T H T T T T)$
$\bullet$ 问题二:
给定上述模型,若观察到上述抛掷结果,最可能的硬币选择序列(状态转换序列)是什么?
$\bullet$ 问题三:
若上述模型中的状态转移矩阵 $A$、状态输出概率 $B$和初始状态分布 $\pi$ 均未知,如何根据观察序列得到它们?
隐马尔可夫模型的三个问题
$\bullet$ 给定HMM $\lambda = ( A, B, \pi )$
给定观察序列 $O = ( o_1 o_2 o_3 \cdots o_T )$
如何有效地计算出观察序列的概率,即 $ P(O|\lambda ) $?
(估算问题) (另一种语言模型)
$\bullet$ 给定 HMM $\lambda = ( A, B, \pi )$
给定观察序列 $ O = ( o_1 o_2 o_3 \cdots o_T )$
如何寻找一个状态转换序列 $q = (q_1 q_2 q_3 \cdots q_T )$,使得该状态转换序列最有可能产生上述观察序列?
(解码问题)
$\bullet$ 在模型参数未知或不准确的情况下,如何根据观察序列
$ O = ( o_1 o_2 o_3 \cdots o_T ) $求得模型参数或调整模型参数,即如何确定一组模型参数,使得 $P (O|\lambda ) $最大?
(学习问题 或 训练问题)
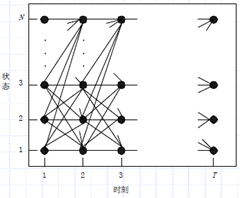
估算观察序列概率
$\bullet$ 对隐马尔可夫模型而言,状态转换序列是隐藏的,一个观察序列可能由任何一种状态转换序列产生。因此要计算一个观察序列的概率值,就必须考虑所有可能的状态转换序列。
$\bullet$ 上图表示了产生观察序列 $ O = ( o_1 o_2 o_3 \cdots o_T )$的所有可能的状态转换序列。
$\bullet$ 给定 $\lambda $, 以及状态转换序列 $q = (q_1 q_2 q_3\cdots q_T )$产生观察序列 $ O = ( o_1 o_2 o_3 \cdots o_T )$的概率可以通过下面的公式计算:
$ P (O|q,\lambda ) = b_{q_1}(o_1) b_{q_2}(o_2) b_{q_3}(o_3) \cdots b_{q_T}(o_T)$
给定 $\lambda $, 状态转换序列 $q = (q_1 q_2 q_3 \cdots q_T )$的概率可以通过下面的公式计算:
$ P (q | \lambda ) = \pi_{q_1} a_{{q_1}{q_2}} a_{{q_2}{q_3}} \cdots a_{q_{T-1}{q_T}}$
则 $O$和 $q$的联合概率为:
$ P (O, q | \lambda ) = P (O|q,\lambda ) P (q | \lambda )$
$\bullet$ 考虑所有的状态转换序列,则
\[P(O|\lambda ) = \sum\limits_q {P(O,q|\lambda )} = \sum\limits_{{q_1}{q_2}, \cdots ,{q_T}} {{\pi _{{q_1}}}{b_{{q_1}}}({o_1}){a_{{q_1}{q_2}}}{b_{{q_2}}}({o_2}) \cdots {a_{{q_{T - 1}}{q_T}}}{b_{{q_{_T}}}}({o_T})} \]
$\bullet$ 理论上,可以通过穷举所有状态转换序列的办法计算观察序列 $O$的概率
$\bullet$ 实际上,这样做并不现实。
可能的状态转换序列共有 $ N^T $个
需要做 $ (2T–1)N^T$次乘法运算,$N^T–1$次加法运算
若 $N = 5,T=100$,则 $(2×100-1)×5^{100}\approx 10^{72}$
$\bullet$ 需要寻找更为有效的计算方法
向前算法
$\bullet$ 向前变量 $\alpha_t(i)$
$\alpha_t(i) = P(o_1 o_2 o_3 \cdots o_t, q_t = i | \lambda)$
$\bullet$ $\alpha_t(i)$的含义是,给定模型 $\lambda$ ,时刻 $t$,处在状态$i$,并且部分观察序列为 $o_1 o_2 o_3 \cdots o_t $的概率。
$\bullet$ 显然有 $\alpha_1(i) = \pi_ib_i(o_1) (1\le i \le N)$
$\bullet$ 若 $\alpha_t(i) (1\le i \le N)$ 已知,如何计算 $\alpha_{t+1}(i)$?
${\alpha _{t + 1}(j)}=\left[ {\sum_{i = 1}^N {{\alpha _t}(i){a_{ij}}} } \right]{b_j}({O_{t + 1}})\;\;\;1 \le t \le T - 1,1 \le j \le N$
向前算法计算步骤
$\1.$ 初始化
$ \alpha_1(i) = \pi_ib_i(o_1) \;\;(1 \le i \le N) $
$\2.$ 迭代计算
${\alpha _{t + 1}(j)}=\left[ {\sum_{i = 1}^N {{\alpha _t}(i){a_{ij}}} } \right]{b_j}({O_{t + 1}})\;\;\;1 \le t \le T - 1,1 \le j \le N$
$\3.$ 终止
$P(O|\lambda) = \sum_{i=1}^N\alpha_T(i) $
向后算法
$\bullet$ 向后变量 $\beta_t(i)$
$\beta_t(i) = P(o_{t+1}o_{t+2} \cdots o_T|q_t = i,\lambda) $
$\bullet$ $\beta_t(i)$的含义是,在给定模型$\lambda$,时刻$t$,处在状态$i$,并且部分观察序列为$ o_{t+1}o_{t+2} \cdots o_T$的概率
$\bullet$ $\beta_T(i)=1(1 \le i \le N)$
$\bullet$ 若 $\beta_{t+1}(j)(1 \le j \le N)$已知,如何计算 $\beta_t(i)$
$\beta_t(i)=\sum_{j=1}^N a_{ij}b_j(o_{t+1}) \beta_{t+1}(j) \;\;\; 1 \le t \le T-1,1 \le j \le N $
向后算法计算步骤
$\1.$ 初始化
$ \beta_T(i) = 1 (1 \le i \le N) $
$\2.$ 迭代计算
$ \beta_t(i) = \sum_{j=1}^N a_{ij}b_j(o_{t+1})\beta_{t+1}(j) \;\;\; 1 \le t\le T-1,1 \le j \le N $
$\3.$ 终止
$ P(O|\lambda) = \sum_{i=1}^N \pi_i b_i(o_1)\beta_1(i) $
求解最佳状态转换序列
$\bullet$ 隐马尔可夫模型的第二个问题是计算出一个能最好解释观察序列的状态转换序列
$\bullet$ 理论上,可以通过枚举所有的状态转换序列,并对每一个状态转换序列 $q$计算 $P(O,q|\lambda)$,能使 $P(O,q|\lambda)$取最大值的状态转换序列 $q^*$就是能最好解释观察序列的状态转换序列,即:
\[{q^*} = \mathop {\arg \max }\limits_q \;P(O,q|\lambda )\]
$\bullet$ 同样,这不是一个有效的计算方法,需要寻找更好的计算方法
维特比算法
$\bullet$ 维特比变量 $ \delta_t(i) $
$\delta_t(i) = \mathop {\max}\limits_{q_1,q_2,\cots,q_{t-1}}\;P(q_1q_2\cdots q_{t-1},q_t=i, o_1o_2\cdots o_t|\lambda) $
$\bullet$ $\delta_t(i)$的含义是,给定模型 $\lambda$,在时刻 $t$处于状态 $i$,观察到 $o_1 o_2 o_3 \cdots o_t$的最佳状态转换序列为 $q_1q_2\cdots q_t$的概率。
$\bullet$ $\delta_1(i) = \pi_ib_i(o_1),\;\; 1 \le i \le N$
$\bullet$ 若 $\delta_t(i)(1 \le i \le N)$已知,如何计算 $\delta_{t+1}(i)$?
$ \delta_{t+1}(j) = \left[{\mathop {\max}\limits_i \;\delta_t(i)a_{ij}\right]b_j(o_{t+1})$
$\bullet$ 如何记录路径? 设定 $T$个数组 $\psi_1(N), \psi_2(N),\cdots,\psi_T(N)$
$\psi_t(i)$记录在时刻 $t$到达状态i的最佳状态转换序列 $t-1$时刻的最佳状态
维特比算法步骤
$\1.$ 初始化
$\delta_1(i)= \pi_ib_i(o_1),\;\;1 \le i \le N$
$\psi_1(i) = 0 $
$\2.$ 迭代计算
${\delta _t}(j) = \mathop {\max }\limits_{1 \le i \le N} \left[ {{\delta _{t - 1}}(i){a_{ij}}} \right]{b_j}({o_t})\;\;\;\;{\psi _t}(j) = \mathop {\arg \max }\limits_{1 \le i \le N} \left[ {{\delta _{t - 1}}{a_{ij}}} \right]$
$\3.$ 终止
$P^* = \mathop {\max}\limits_{1\le i \le N}}\ \left[delta_T(i)\right] \;\;\;q_T^* = \mathop {\arg \max}\limits_{1 \le i \le N}}\ \left[delta_T(i)\right]$
$\4.$ 求解最佳路径
$q_t^* = \psi_{t+1}(q_{t+1}^*),\;\; t=T-1,T-2,\codts,1$
参数学习
$\bullet$ 隐马尔科夫模型的第三个问题是如何根据观察序列 $O =( o_1 o_2 o_3 \cdots o_T ) $求得模型参数或调整模型参数,即如何确定一组模型参数使得 $P (O|\lambda )$最大?
$\bullet$ 隐马尔科夫模型的前两个问题均假设模型参数已知,第三个问题是模型参数未知,求最佳模型的问题,是三个问题中最为困难的问题
有指导的参数学习
$\bullet$ 在模型 $\lambda$未知的情况下,如果给定观察序列的同时,也给定了状态转换序列,此时可以通过有指导的学习方法学习模型参数。例如给定下面的训练数据,可以通过最大似然估计法估计模型参数:
$ H/1 \;\; H/1\;\; T/1\;\; T/2\;\; H/3 \;\; T/5 …$
$ T/2 \;\; H/1 \;\; T/2 \;\; H/3 \;\; H/3 \;\; H/1 … $
$\bullet$ 参数学习非常简单,在训练数据足够大的前提下,效果不错
$\bullet$ 缺点,状态信息未知时无法使用。或者要由人工标注状态信息,代价高
$\bullet$ 在NLP中,在无指导学习效果不佳时,需要采用有指导学习
无指导的参数学习
$\bullet$ 在模型 $\lambda$未知的情况下,如果仅仅给定了观察序列,此时学习模型的方法被称做无指导的学习方法
$\bullet$ 对于隐马尔科夫模型而言,采用无指导学习方法,没有解析方法。通常要首先给定一组不准确的参数,再通过反复迭代逐步求精的方式调整模型参数,最终使参数稳定在一个可以接受的精度
$\bullet$ 利用无指导的学习方法估计隐马尔科夫模型参数时,并不能一定保证求得最优模型,一般能得到一个局部最优模型
直观的想法
$\bullet$ 给定一组初始参数 $(A\; B\; \pi)$
$\bullet$ 由于没有给定状态转换序列,无法计算状态转移的频率、状态输出的频率以及初始状态频率
$\bullet$ 假定任何一种状态转换序列都可能
$\bullet$ 对每种状态转换序列中的频次加权处理,计算状态转移、状态输出、以及初始状态的期望频次
$\bullet$ 利用计算出的期望频次更新 $(A\;B\;\pi)$
$\bullet$ 权值如何选择
对状态转换序列 $q$而言,选择 $P(q|O,\lambda) $
$\bullet$ 理论上可行,现实不可行,要考虑所有的状态转移路径需要多次迭代,问题更为严重
$\bullet$ 需要更为有效的算法,即Baum-Welch算法
Baum-Welch Algorithm
$\bullet$ 定义变量 $\xi_t(i,j)$
$\xi_t(i,j) = P(q_t=i,q_{t+1}=j|O,\lambda) $
$\bullet$ $\xi_t(i,j) = P(q_t=i,q_{t+1}=j|O,\lambda) $含义是,给定模型 $\lambda$和观察序列 $O$,在时刻 $t$处在状态 $i$,时刻 $t+1$处在状态 $j$的期望概率
$\bullet$ $\xi_t(i,j)$可以进一步写成:
\[{\xi _t}(i,j) = \frac{{P({q_t} = i,{q_{t + 1}} = j,O|\lambda )}}{{P(O|\lambda )}} = \frac{{{\alpha _t}(i){a_{ij}}{b_j}({o_{t + 1}}){\beta _{t + 1}}(j)}}{{P(O|\lambda )}}= \frac{{{\alpha _t}(i){a_{ij}}{b_j}({o_{t + 1}}){\beta _{t + 1}}(j)}}{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _t}(i){a_{ij}}{b_j}({o_{t + 1}}){\beta _{t + 1}}(j)} } }}\]
$\bullet$ 定义变量 $\gamma_t(i)$,令其表示在给定模型以及观察序列的情况下,$t$时刻处在状态 $i$的概率,则有:
\[\gamma_t(i) = \sum_{j=1}^N \xi_t(i,j) \]
$\sum_{t=1}^{T-1} \gamma_t(i) $观察序列 $O$中从状态 $i$出发的转换的期望概率
$\sum_{t=1}^{T-1} \xi_t(i,j) $观察序列 $O$中从状态 $i$到状态 $j$的转换的期望概率
$\bullet$ 关于 $\pi, A, B$,一种合理的估计方法如下
$\bullet$ 利用上述结论,即可进行模型估算
$\bullet$ 选择模型参数初始值,初始值应满足隐马尔科夫模型的要求,即:
\[ \sum_{i=1}^N \pi_i = 1\;\;\; \sum_{j=1}^N \a_{ij} =1,\; 1 \le i \le N\;\; \sum_{k=1}^M b_j(k)=1,\;1 \le j \le N \]
$\bullet$ 将初始值代入前面的公式中,计算一组新的参数 $\overline{\pi},\overline{A},\overline{B} $
$\bullet$ 再将新的参数代入,再次计算更新的参数
$\bullet$ 如此反复,直到参数收敛
$\bullet$ Baum-Welch算法是一种EM算法
$\bullet$ E-step:计算 $\xi_t(i, j)$和 $\gamma_t(i) $
$\bullet$ M-step:估计模型 $\overline{\lambda}$
$\bullet$ 终止条件 $|\log(P(O|\lambda_{i+1})) - \log(P(O|\lambda_i))| < \varepsilon $
$\bullet$ Baum等人证明要么估算值 $\overline{\lambda}}$和估算前的参数值 $\lambda$相等,要么估算值 $\overline{\lambda}}$比估算前的参数值 $\lambda$更好的解释了观察序列 $O$
$\bullet$ 参数最终的收敛点并不一定是一个全局最优值,但一定是一个局部最优值
L.R.Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech recognition, Proc. IEEE, 77(2): 257-286, 1989
隐马尔科夫模型的实现
$\bullet$ 浮点溢出问题
- 对于韦特比算法,采用取对数的方式
- 对于Baum-Welch算法,采用放大因子
- 对于向前算法采用放大因子以及取对数的方式。