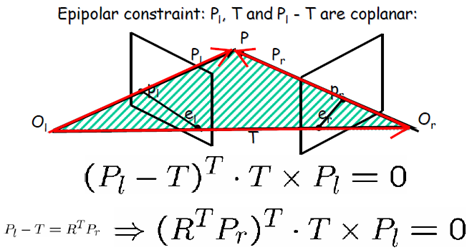
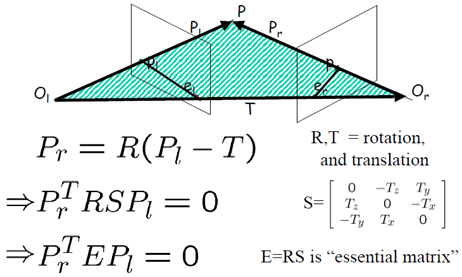
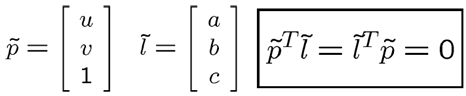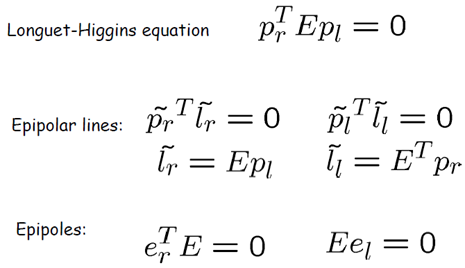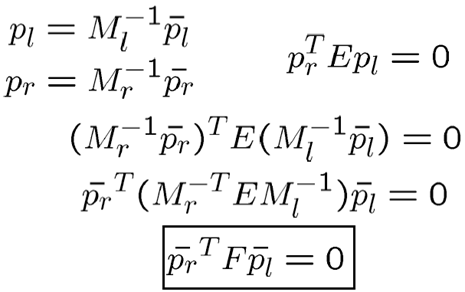回顾本质矩阵的定义
本质矩阵的基本性质:
结合成像的几何关系
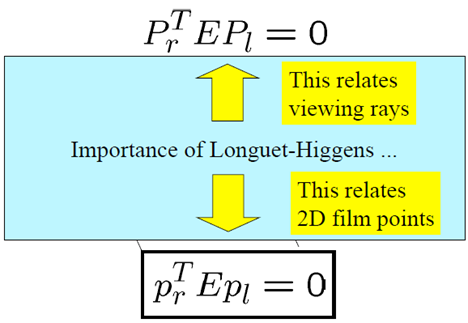
Longuet-Higgins equation
注意大小写的区别哦,大小表示物点矢量,小与表示像点矢量。
像平面上的一点可以看作:
• (u,v) 2D film point(局限于像平面上来考虑)
• (u,v,f) 3D point on film plane(相机坐标系中来考虑)
• k(u,v,f) viewing ray into the scene(透过像点和原点射线上点的像,相机坐标系中来考虑)
• k(X, Y, Z) ray through point P in the scene(在世界坐标系中来考虑)
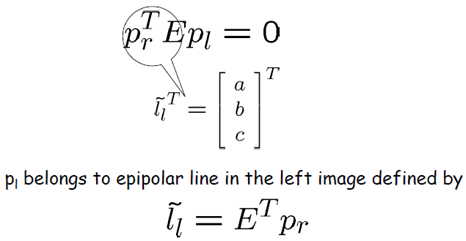
设$l$为像平面上的一直线:$au+bv+c=0$
由点线结合关系可得:
因此有
这样就可以用几何的观点来解释上述方程:左像平面上的一点$p_l$乘以本质矩阵$E$,结果为一条直线,该直线就是$p_l$的极线,且过$p_l$在右像平面上的对应点$p_r$。这个结论十分喜人。
同理有
• Remember: epipoles belong to the epipolar lines
• And they belong to all the epipolar lines
关于本质矩阵的关系总结如下:
本质矩阵采用的是相机的外部参数,也就是说采用相机坐标(The essential matrix uses CAMERA coordinates),如果要分析数字图像,则要考虑坐标(u,v),此时需要用到内部参数(To use image coordinates we must consider the INTRINSIC camera parameters)
从像素级来考虑,有如下关系
short version: The same equation works in pixel coordinates too!
矩阵$F$称为基本矩阵:$ F=M_r^{-T}RSM_l^{-1} $
• has rank 2
• depends on the INTRINSIC and EXTRINSIC Parameters (f, etc ; R & T)
Analogous to essential matrix. The fundamental matrix also tells how pixels (points) in each image are related to epipolar lines in the other image.
例子:
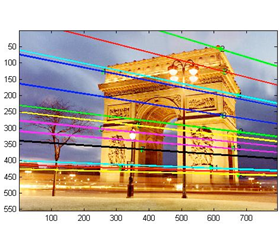
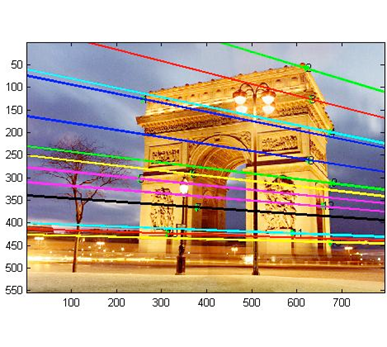
由$ F*e_l =0 $,并根据下图,where is the epipole? vector in the right nullspace of matrix $F$,即$F$的右零空间。当然$e_l$是非零向量,也就是说$ F*e_l =0 $有非零解,说明矩阵$F$不是满秩的,或者说它是奇异的,However, due to noise,F may not be singular.So instead, next best thing is eigenvector associated with smallest eigenvalue of F。
>> [u,d] = eigs(F’ * F)
u =
-0.0013 0.2586 -0.9660
0.0029 -0.9660 -0.2586
1.0000 0.0032 -0.0005
d = 1.0e8*
-1.0000 0 0
0 -0.0000 0
0 0 -0.0000
eigenvector associated with smallest eigenvalue
>> uu = u(:,3)
uu = ( -0.9660 -0.2586 -0.0005)
>> uu / uu(3) : to get pixel coords
(1861.02 498.21 1.0)
where is the epipole?
相反的问题是:如果已知点的对应关系,如何计算本质矩阵和基本矩阵呢:
下一节:计算机视觉基础6——本质矩阵和基本矩阵的求解