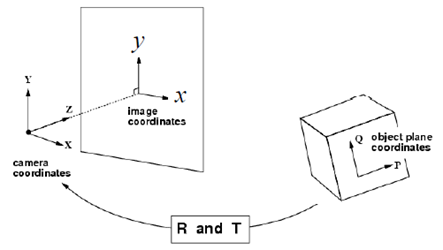
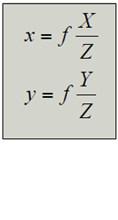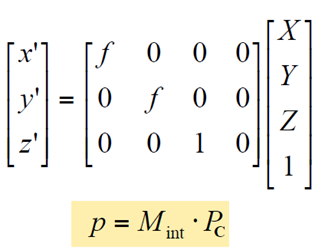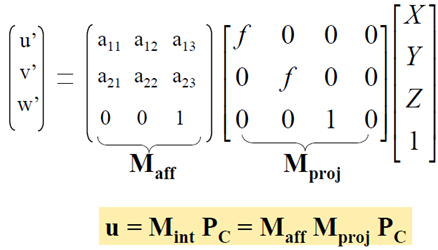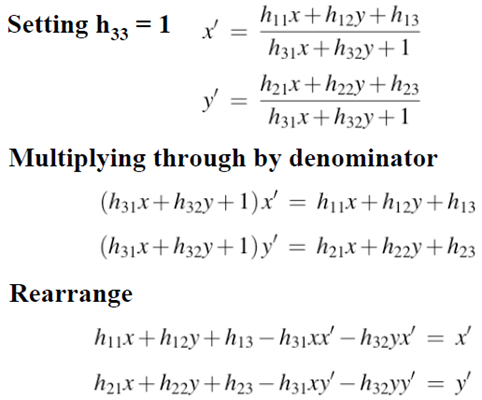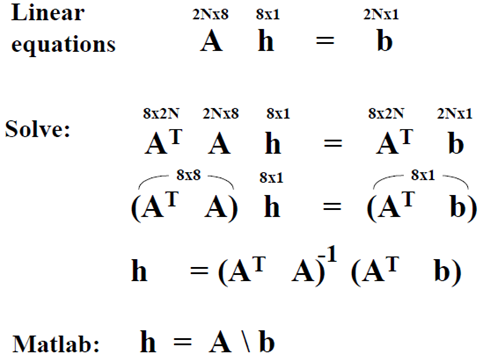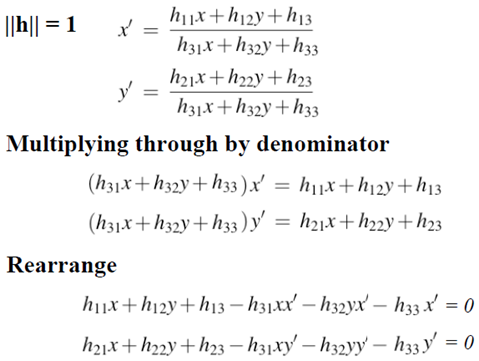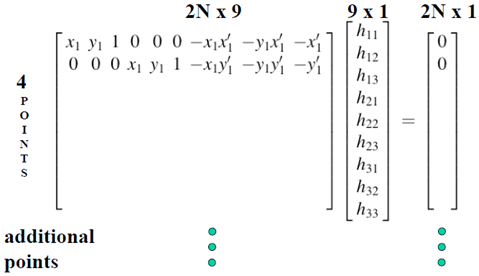在前面已经讨论了三维物体成像过程,相比之下,还有一种稍简单的情况——平面成像,即所有的物点都处在同一个平面上,我们有理由相信,这种情况下的成像关系是一般立体成像的一种特例。
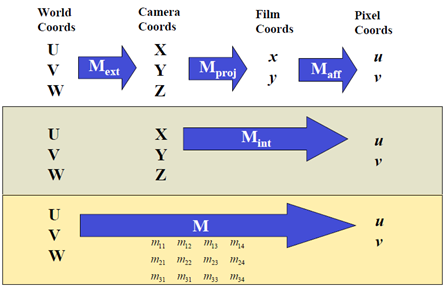
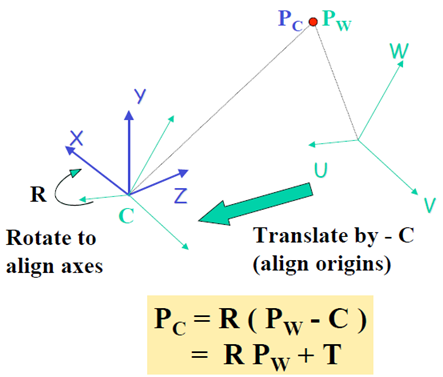
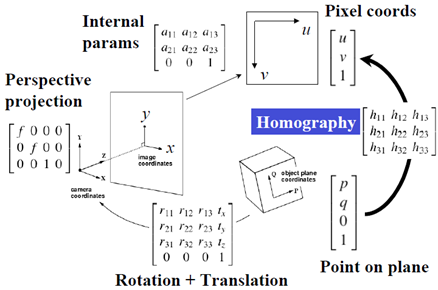
先回顾一下一般的单体成像过程
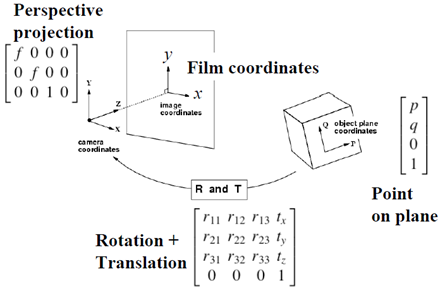
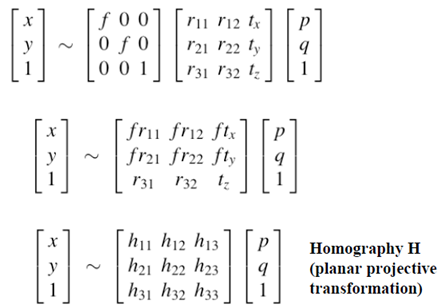
对于共面的物点,在恰当的世界坐标系中,可以令其中一个坐标值为0,不妨设第三维坐标为0,图示如下:
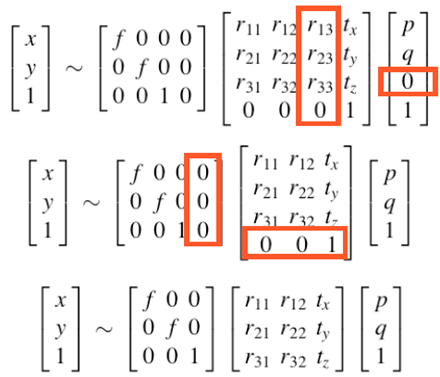
由于物点的第三维坐标为0,整个成像过程的矩阵表示会得到简化。
可以简化为一个3X3的矩阵,称之为Homography矩阵,该矩阵是可逆的!!
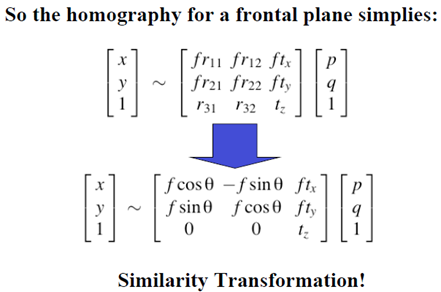
对于正前方的物体平面(垂直于光轴),成像关系将更进一步简化。
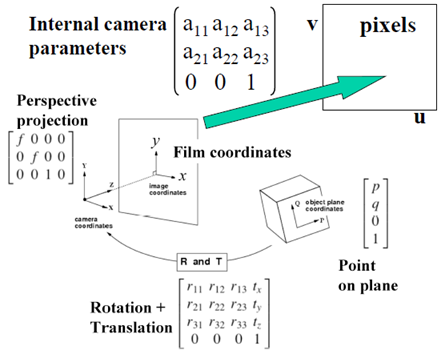
将共面物点经成像之后,再变换为数字图像(u,v)
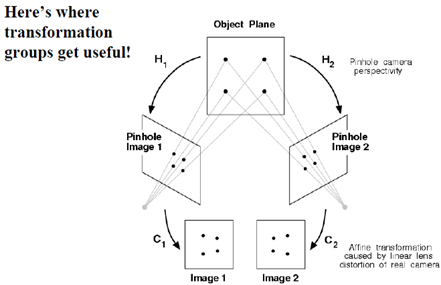
研究共面点成像有什么意义呢?
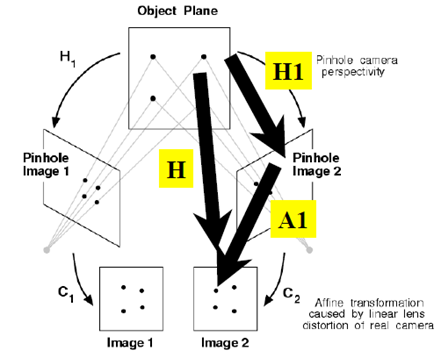
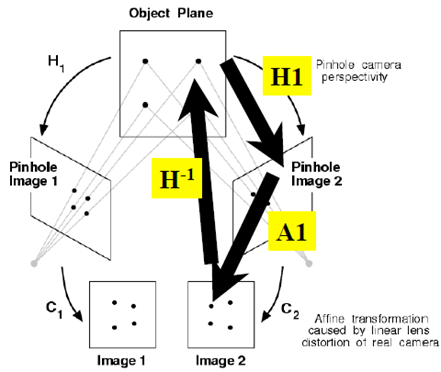
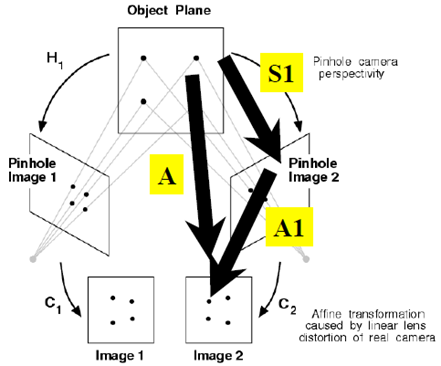
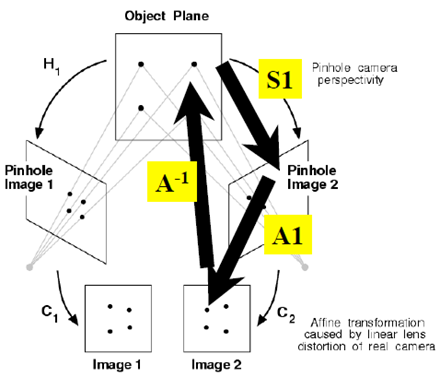
原来是为了研究两幅图之间的关系!共面点成像过程总结如下:
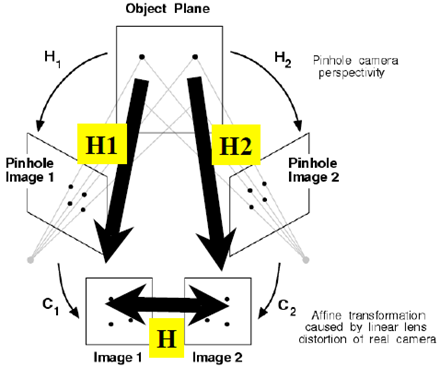
应用之一:消除透视投影的失真
应用之二:图像拼接
在这些应用中,需要解决两个关键问题:
1. 如何确定两幅图像之间的变换关系(需要多少个已知点?如何计算?)
2. 如何生成新的像素点,即在拉伸或拼接之后,需要生成新的像素点。
选择第一种约束关系
可以写在线性方程组或矩阵的形式
在实际求解变换矩阵时,需要考虑数值计算的问题。
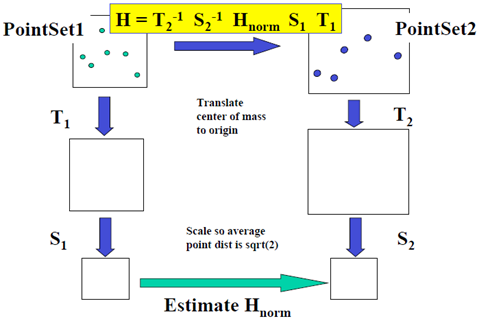
R.Hartley: “In Defense of the Eight Point Algorithm”
Observation: Linear estimation of projective transformation parameters from point correspondences often suffer from poor “conditioning” of the matrices involves. This means the solution is sensitive to noise in the points (even if there are no outliers).
To get better answers, precondition the matrices by performing a normalization of each point set by:
• translating center of mass to the origin
• scaling so that average distance of points from origin is sqrt(2).
• do this normalization to each point set independently
采用第二种约束关系