图论算法-深度优先搜索的应用
深度优先生成树
深度优先生成树(depth-first spanning tree)的步骤:一个图从顶点开始生成树,则A就是该树的根,是第一个没访问到的顶点。图中的每一条边都出现在树上。如果当我们处理时,发现是未被标记的,或当我们处理时发现是未标记的,那么我们就用树的一条边表示它。如果当我们处理时发现已被标记,并且当我们处理时发现也已有标记,那么我们就画一条虚线,并称之为背向边(back edge),表示这条“边”实际上不是树的一部分。
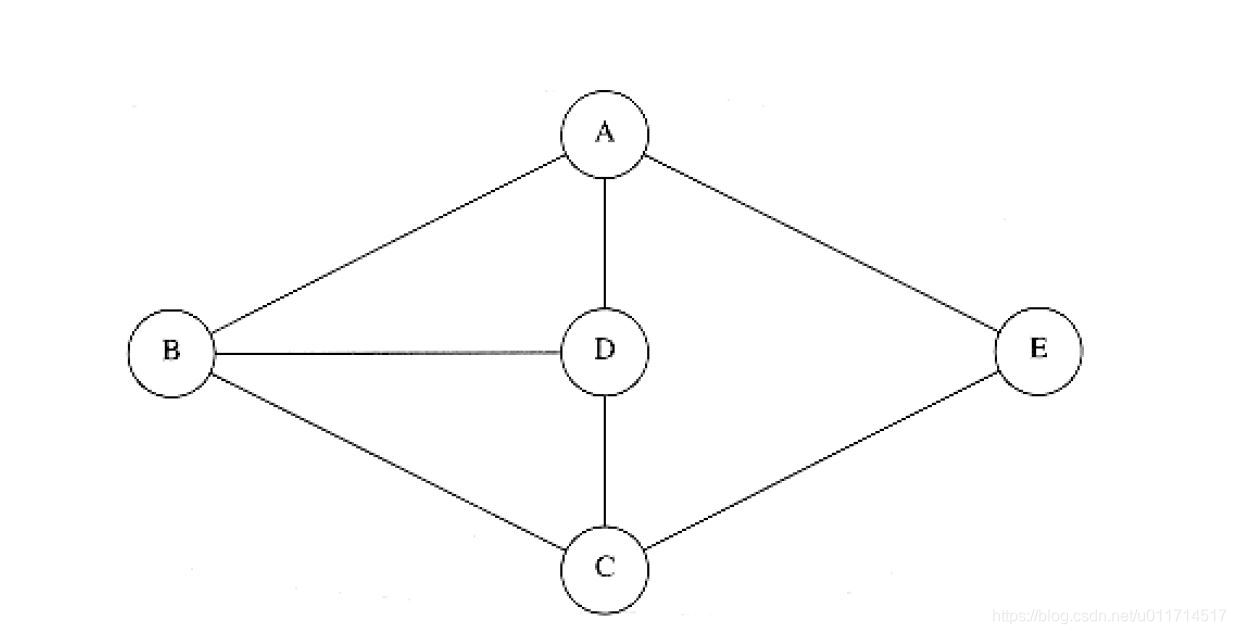
双连通性
如果一个连通的无向图中的任一顶点删除之后,剩下的图仍然连通,那么这样的无向连通图就称为是双连通(biconnected)。
如果一个图不是双连通的,那么,将其删除后图将不再连通的那些顶点叫做割点(articulation point)。
深度优先搜索提供一种找出连通图中的所有割点的线性时间算法。首先,从图中任一顶点开始,执行深度优先搜索并在顶点被访问时给他们编号。对于每一个顶点我们称其先序编号为。然后,对于深度优先搜索生成树上的每一个顶点,计算编号最低的顶点,我们称之为,该点从开始,通过树的零条或多条边且可能还有一条背向边而达到。
根据定义可知是
- 所有背向边中的最低
- 树的所有边中最低
中的最小者。
伪代码
在一次深度优先搜索中对割点的检测
void FindArt(Vertex v)
{
Vertex w;
Visited[v] = True;
Low[v] = Num[v] Counter++; // Rule 1
for each w adjacent to v
{
if(Visited[w]==0) // Forward edge
{
Parent[w] = v;
FindArt(w);
if(Low[w] >= Num[v])
printf("%v is an articulation point
", v);
Low[v] = Min(Low[v], Low[w]); // Role 3
}
else
if(Parent[v] != w) // Back edge
Low[v] = Min(Low[v], Num[w]); // Role 2
}
}
欧拉回路
在图中找出一条路径,使得该路径对图的每条边恰好访问一次。这种图论问题在1736年由欧拉解决,它标志着图论的诞生。根据特定问题的叙述不同,这种问题通常叫做*欧拉路径(Euler path,有时称欧拉环游—Euler tour)或欧拉回路(Euler circuit)*问题。
- 其终点必须终止在起点上的欧拉回路只有当图是连通的并且每个顶点的度是偶数时才可能存在。
- 如果恰好两个顶点的度是奇数,那么当我们从一个奇数度的顶点出发最后终止在另一个奇数度的顶点时,仍有可能得到一个欧拉环游。这里,欧拉环游是必须访问图的每一边但最后不一定必须回到起点的路径。如果奇数度的顶点多于两个,那么欧拉环游也是不可能存在的。
- 所有顶点的度均为偶数的任何连通图必然有欧拉回路。
完整代码
#include <stdio.h>
#include <stdlib.h>
#include "graph.h"
#include "list.h"
struct VertexCell
{
VertexType data;
Arc next;
};
struct ArcCell
{
//WeightType weight;
VertexType adjver;
Arc next;
};
struct GraphCell
{
Vertex ver;
int vernum;
int arcnum;
};
struct ListCell
{
ElementType Element;
List next;
};
List CreateList(void)
{
List L;
L = (List)malloc(sizeof(struct ListCell));
L->next = NULL;
return L;
}
void Insert(ElementType X, List L)
{
List tmp, p;
tmp = CreateList();
tmp->Element = X;
p = L;
while (p->next != NULL)
p = p->next;
p->next = tmp;
}
void Merge(List L, List E)
{
List p, e, l;
p = L;
while (p->next != NULL && p->Element != E->next->Element)
p = p->next;
l = p->next;
p->next = E->next->next;
e = E;
while (e->next != NULL)
e = e->next;
e->next = l;
}
void PrintList(List L)
{
List p;
p = L->next;
while (p != NULL)
{
printf("%d ", p->Element);
p = p->next;
}
printf("
");
}
Graph CreateGraph(void)
{
int i;
Graph G;
VertexType v, w;
Arc edge;
G = (Graph)malloc(sizeof(struct GraphCell));
printf("Input vernum: ");
scanf("%d", &G->vernum);
G->ver = (Vertex)malloc(sizeof(struct VertexCell) * (G->vernum + 1));
for (i = 0; i <= G->vernum; i++)
{
G->ver[i].data = i;
G->ver[i].next = NULL;
}
printf("Input arcnum: ");
scanf("%d", &G->arcnum);
for (i = 1; i <= G->arcnum; i++)
{
scanf("%d%d", &v, &w);
edge = (Arc)malloc(sizeof(struct ArcCell));
edge->adjver = w;
edge->next = G->ver[v].next;
G->ver[v].next = edge;
edge = (Arc)malloc(sizeof(struct ArcCell));
edge->adjver = v;
edge->next = G->ver[w].next;
G->ver[w].next = edge;
}
return G;
}
void PrintGraph(Graph G)
{
Arc edge;
int i;
for (i = 1; i <= G->vernum; i++)
{
printf("%d:", G->ver[i].data);
edge = G->ver[i].next;
while (edge != NULL)
{
printf("%d->", edge->adjver);
edge = edge->next;
}
printf("^
");
}
}
void DeleteArc(Graph G, VertexType head, VertexType tail)
{
Arc edge, pre;
pre = &G->ver[head];
edge = G->ver[head].next;
while (edge->adjver != tail)
{
pre = edge;
edge = edge->next;
}
pre->next = edge->next;
free(edge);
pre = &G->ver[tail];
edge = G->ver[tail].next;
while (edge->adjver != head)
{
pre = edge;
edge = edge->next;
}
pre->next = edge->next;
free(edge);
}
int HasEulerCircuit(Graph G)
{
int degree[G->vernum + 1];
int i;
Arc edge;
for (i = 1; i <= G->vernum; i++)
degree[i] = 0;
for (i = 1; i <= G->vernum; i++)
{
edge = G->ver[i].next;
while (edge != NULL)
{
degree[i] += 1;
degree[edge->adjver] += 1;
edge = edge->next;
}
}
for (i = 1; i <= G->vernum; i++)
if (degree[i] != 0)
break;
if (i > G->vernum)
return 0;
for (i = 1; i <= G->vernum; i++)
{
if (degree[i] != 0 && (degree[i] / 2) % 2 == 1)
return 0;
}
return 1;
}
void EulerCircuit(Graph G, VertexType s)
{
List L, E;
L = CreateList();
Insert(s, L);
while (HasEulerCircuit(G))
{
s = NextStart(L, G);
E = NextEulerCircuit(G, s);
Merge(L, E);
//PrintGraph(G);
}
PrintList(L);
}
VertexType NextStart(List L, Graph G)
{
List p;
p = L->next;
while (p != NULL)
{
if (G->ver[p->Element].next != NULL)
return p->Element;
p = p->next;
}
return 0; // 返回 0 表示没有顶点可用了
}
List NextEulerCircuit(Graph G, VertexType s)
{
List L;
Arc edge;
VertexType tail;
VertexType start;
start = s;
L = CreateList();
Insert(s, L);
while (tail != start)
{
edge = G->ver[s].next;
tail = edge->adjver;
Insert(tail, L);
DeleteArc(G, s, tail);
//PrintGraph(G);
s = tail;
}
return L;
}
int main()
{
Graph G;
G = CreateGraph();
PrintGraph(G);
EulerCircuit(G, 5); // 从顶点5开始查找欧拉回路
return 0;
}
输入/输出
Input vernum: 12
Input arcnum: 21
1 3
1 4
2 3
2 8
3 4
3 6
3 7
3 9
4 5
4 7
4 10
4 11
5 10
6 9
7 9
7 10
8 9
9 10
9 12
10 11
10 12
Adajacency list:
1:4->3->^
2:8->3->^
3:9->7->6->4->2->1->^
4:11->10->7->5->3->1->^
5:10->4->^
6:9->3->^
7:10->9->4->3->^
8:9->2->^
9:12->10->8->7->6->3->^
10:12->11->9->7->5->4->^
11:10->4->^
12:10->9->^
Euler Circuit:
5 10 12 9 10 11 4 3 1 4 10 7 9 8 2 3 9 6 3 7 4 5
有向图
利用和无向图相同的思路,也可以通过深度优先搜索以线性时间遍历有向图。如果图不是强连通的,那么从某个节点开始的深度优先搜索可能访问不了所有的节点。在这种情况下我们在某个未作标记的节点处开始,反复执行深度优先搜索,直到所有的节点都被访问到。
存在三种类型的边并不通向新的顶点。首先是一些背向边(back edge);还有一些前向边(forward edge),它们从树的一个节点通向一个后裔;最后就是一些交叉边(cross edge),它们把不直接相关的两个树节点连接起来。深度优先搜索森林一般通过把一些子节点和一些新的树从左到右添加到森林中形成。
深度优先搜索的一种用途是检测一个有向图是否是无圈图,法则如下:一个有向图是无圈图当且仅当它没有背向边。
查找强分支
通过执行两次深度优先搜索,我们可以检测一个有向图是否是强连通的,如果它不是强连通的,那么我们实际上可以得到顶点的一些子集,它们到其自身是强连通的。这也可以只用一次深度优先搜索做到。
首先,在输入的图G上执行一次深度优先搜索。通过对深度优先生成森林的后序遍历将G的顶点编号,然后把G的所有的边反向,形成。
该算法通过对G_r执行一次深度搜先搜索而完成,总是在编号最高的顶点开始一次新的深度优先搜索。
完整代码
#include <stdio.h>
#include <stdlib.h>
#include "graph.h"
struct VertexCell
{
VertexType data;
Arc first;
};
struct ArcCell
{
//WeightType weight;
VertexType adjver;
Arc next;
};
struct GraphCell
{
Vertex ver;
int vernum;
int arcnum;
};
struct ListCell
{
ElementType ver;
List next;
};
List CreateList(void)
{
List L;
L = (List)malloc(sizeof(struct ListCell));
L->ver = 0; // 头节点的数据域当作长度
L->next = NULL;
return L;
}
void Insert(ElementType X, List L)
{
Position p, t;
p = CreateList();
p->ver = X;
t = L;
while (t->next != NULL)
t = t->next;
t->next = p;
p->next = NULL;
L->ver++;
}
void PrintList(List L)
{
Position p;
p = L->next;
while (p != NULL)
{
printf("%d ", p->ver);
p = p->next;
}
printf("
");
}
void DisposeList(List L)
{
Position p, tmp;
if (L != NULL)
{
p = L->next;
while (p != NULL)
{
tmp = p;
p = p->next;
free(tmp);
}
L->next = NULL;
}
}
Graph CreateGraph(void)
{
int i;
Graph G;
VertexType v, w;
Arc edge;
G = (Graph)malloc(sizeof(struct GraphCell));
printf("Input vernum: ");
scanf("%d", &G->vernum);
G->ver = (Vertex)malloc(sizeof(struct VertexCell) * (G->vernum + 1));
for (i = 0; i <= G->vernum; i++)
{
G->ver[i].data = i;
G->ver[i].first = NULL;
}
printf("Input arcnum: ");
scanf("%d", &G->arcnum);
for (i = 1; i <= G->arcnum; i++)
{
scanf("%d%d", &v, &w);
edge = (Arc)malloc(sizeof(struct ArcCell));
edge->adjver = w;
edge->next = G->ver[v].first;
G->ver[v].first = edge;
}
return G;
}
void PrintGraph(Graph G)
{
Arc edge;
int i;
for (i = 1; i <= G->vernum; i++)
{
printf("%d:", G->ver[i].data);
edge = G->ver[i].first;
while (edge != NULL)
{
printf("%d->", edge->adjver);
edge = edge->next;
}
printf("^
");
}
}
int visited[VERNUM];
void Dfs(Graph G, VertexType v, List L)
{
Arc edge;
visited[v] = 1;
Insert(v, L);
edge = G->ver[v].first;
while (edge != NULL)
{
if (visited[edge->adjver] == 0)
Dfs(G, edge->adjver, L);
edge = edge->next;
}
}
Graph ReverseGraph(Graph G)
{
Graph Gr;
int i;
Arc Ge, Gre;
Gr = (Graph)malloc(sizeof(struct GraphCell));
Gr->vernum = G->vernum;
Gr->ver = (Vertex)malloc(sizeof(struct VertexCell) * (Gr->vernum + 1));
for (i = 0; i <= Gr->vernum; i++)
{
Gr->ver[i].first = NULL;
Gr->ver[i].data = i;
}
Gr->arcnum = G->arcnum;
for (i = 1; i <= Gr->vernum; i++)
{
Ge = G->ver[i].first;
while (Ge != NULL)
{
Gre = (Arc)malloc(sizeof(struct ArcCell));
Gre->adjver = i;
Gre->next = Gr->ver[Ge->adjver].first;
Gr->ver[Ge->adjver].first = Gre;
Ge = Ge->next;
}
}
return Gr;
}
int main()
{
Graph G, Gr;
List L, T;
Position p;
int i;
G = CreateGraph();// 创建一个图 手动输入顶点及边
PrintGraph(G); // 打印输出图的邻接表
L = CreateList(); // 使用链表存储深度优先搜索的序列号
Dfs(G, 7, L); // 将生成的序列存储在 L 中
PrintList(L); // 输出序列号
Gr = ReverseGraph(G); // 将有向图 G 的边反转得到 Gr
PrintGraph(Gr); // 输出反转后的图的邻接表
// 将深度优先搜索用来标记每个顶点是否得到访问的数组重新全部赋值为 0
// 因为对新图Gr进行深度优先搜索
for (i = 0; i < VERNUM; i++)
visited[i] = 0;
T = CreateList();
// 深度优先搜索每个顶点
p = L->next;
while (p != NULL)
{
if (visited[p->ver] == 0)
Dfs(Gr, p->ver, T);
if (T->next != NULL)
{
PrintList(T);
DisposeList(T);
}
p = p->next;
}
system("pause");
return 0;
}
输入/输出
Input vernum: 10
Input arcnum: 15
1 2
1 4
2 3
2 6
3 1
3 4
3 5
4 5
6 3
7 6
7 8
8 6
8 10
9 8
10 9
Adjacency list G:
1:4->2->^
2:6->3->^
3:5->4->1->^
4:5->^
5:^
6:3->^
7:8->6->^
8:10->6->^
9:8->^
10:9->^
Depth-first search G:
7 8 10 9 6 3 5 4 1 2
Reverse graph G,
Adjacency list Gr:
1:3->^
2:1->^
3:6->2->^
4:3->1->^
5:4->3->^
6:8->7->2->^
7:^
8:9->7->^
9:10->^
10:8->^
Connected branch:
7
8 9 10
6 2 1 3
5 4
请按任意键继续. . .
由最后输出可得此图有4个连通分支,每行打印输出一个连通分支的所有顶点。