现在是晚上十二点半,好累(无奈脸),接着给各位——也是给自己,更新笔记吧~
序列型状态划分:
经典例题:乘积最大(Luogu 1018)
* 设有一个长度为 N 的数字串,要求选手使用 K 个乘号将它分成 K+1 个部分,找出一种分法,使得这 K+1 个部分的乘积能够为最大。
* 例如,有一个数字串: 312,当 N=3, K=1 时会有以下两种分法:
1 3×12=36
2 31×2=62
* 符合题目要求的结果是: 31×2=62
* 现在,请你帮助你的好朋友 XZ 设计一个程序,求得正确的答案。
* 题目中要求把整个序列有序地切分成 K+1 个部分。
* 状态设计:设我们把前 F[i][j] 为前 i 个数字切成 j 部分所能得到的最大乘积。
* 很显然这时候我们只需要通过枚举最后一部分的数字有多大,就能得到结果乘积了。(满足最优性)
1 //T20:乘积最大(DP) 2 ++k;//K+1 3 f[0][0]=1;//初值 4 for(int i=1;i<=n;++i)//枚举长度 5 for(int j=1;j<=k;++j)//枚举切割部分 6 for(int l=0;l<i;++l)//枚举前一块的最后位置(可以从0开始) 7 f[i][j]=max(f[i][j],f[l][j-1]*val(l+1,i));//val(a,b)表示a~b之间形成的数 8 cout<<f[n][k]<<endl;//答案
为什么不设计状态为 F[i][j][k],表示把 i 到 j 的数字切成 k 块?
因为不需要求出中间一块要被一个*号截开的情况,没必要求出中间一块[i,j]的最大乘积。
经典例题:数字游戏(Luogu 1043)
丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单,但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的,在你面前有一圈整数(一共 n 个),你要按顺序将其分为m 个部分,各部分内的数字相加,相加所得的 m 个结果对 10 取模后再相乘,最终得到一个数 k。游戏的要求是使你所得的 k 最大或者最小。
例如,对于下面这圈数字( n=4, m=2):
要求最小值时, ((2-1) mod 10)×((4+3) mod 10)=1×7=7,要求最大值时,为 ((2+4+3) mod 10)×(-1 mod 10)=9×9=81。特别值得注意的是,无论是负数还是正数,对 10 取模的结果均为非负值。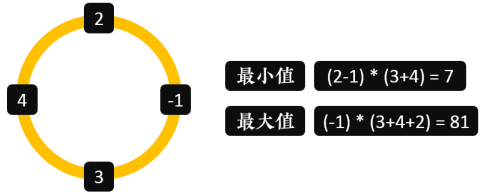
* 题目中要求把整个环形序列切分成 m 个部分;先不考虑环形的问题,假若是对于一个线形序列,如何做?
* 状态设计:参考前一道题目的做法,设我们把前 F[i][j] 为前 i 个数字切成 j 部分所能得到的最大乘积。
* 很显然这时候我们只需要通过枚举最后一部分的数字有多大,就能得到结果乘积了。 (满足最优性)
* 环形序列:第一个位置不一定是开头,有可能位于序列的中间。
* 解决方法:枚举每一个位置,把它当作开头算一遍,得到的结果取最大值即为答案。
当出现循环节时候,我们就可以用“复制一遍序列”的方法来做,这样就可以实现头尾相接,如下图: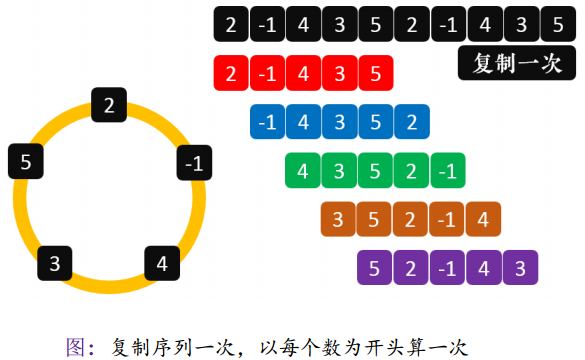
对于每一条链,像上一题那样做就OK!
1 //T21:数字游戏(DP) 2 void work(int *a)//预处理过程 3 { 4 s[0]=0;//预处理前缀和 5 for(int i=1;i<=n;++i) s[i]=s[i-1]+a[i]; 6 for(int i=0;i<=n;++i) 7 for(int j=0;j<=m;++j) 8 f[i][j]=0,g[i][j]=INF;//初值 9 f[0][0]=g[0][0]=1;//初值 10 ...//DP过程 11 }
1 //T21:数字游戏(DP) 2 void work(int *a) 3 { 4 ...//初值,预处理 5 for(int i=1;i<=n;++i) 6 for(int j=1;j<=m;++j) 7 for(int k=0;k<i;++k)//分别计算最大值和最小值 8 { 9 //问题:为什么f不用判断而g需要判断,最大值的话也是不合法的,但是对答案没啥影响,因为0肯定不是最大值 10 f[i][j]=max(f[i][j],f[k][j-1]*(((s[i]-s[k])%10+10)%10)); 11 if(g[k][j-1]!=INF)//g[k][j-1]=INF代表前k个不能切成j-1个部分,当i到k这一段为0的时候,前面一段的最小值=inf会有问题 12 g[i][j]=min(g[i][j],g[k][j-1]*(((s[i]-s[k])%10+10)%10)); 13 } 14 amax=max(amax,f[n][m]);//全局最大值 15 amin=min(amin,g[n][m]);//全局最小值 16 }
1 //T21:数字游戏(DP) 2 //主程序 3 cin>>n>>m; 4 for(int i=1;i<=n;++i) cin>>a[i],a[n+i]=a[i];//复制一遍 5 amax=0; 6 amin=INF;//初值 7 for(int i=1;i<=n;++i)//以每个位置开始计算(以a[i-1]为开头的数组(指针)保证枚举每一条链) 8 { 9 work(a+i-1); 10 } 11 cout<<amin<<endl<<amax<<endl;
经典例题:能量项链(Luogu 1063)
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链。在项链上有 N 颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为 m,尾标记为r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为m*r*n( Mars 单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时, Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4, 4 颗珠子的头标记与尾标记依次为 (2, 3) (3, 5) (5,10) (10, 2)。我们用记号 ⊕ 表示两颗珠子的聚合操作, (j⊕k) 表示第 j, k 两颗珠子聚合后所释放的能量。则第 4、 1 两颗珠子聚合后释放的能量为:
- (4⊕1)=10*2*3=60
*这一串项链可以得到最优值的一个聚合顺序所释放的总能量为:
- ((4⊕1)⊕2)⊕3) =10*2*3+10*3*5+10*5*10=710
* 环形序列:枚举每一个位置,把它当作开头算一遍,得到的结果取最大值即为答案。
* 那么我们只需要考虑线性序列的问题了。
如上题做法,我们还是把这个序列复制一遍,最后剩下的珠子为最后一个数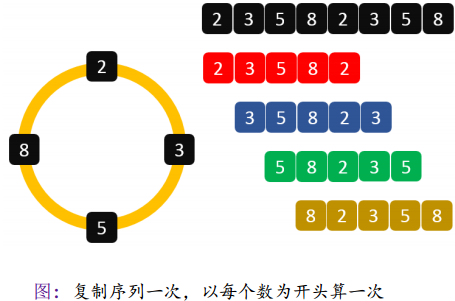
* 状态设计:设 F[i][j] 为把 i 到 j 之间的珠子合并起来,所能释放的最大能量。
* 问题:为什么不能只设 F[i] 代表前 i 个珠子合并的最大能量。
- 因为和合并的方式有关。
* 状态转移:枚举最后一颗和 i, j 一同合并的珠子 k。
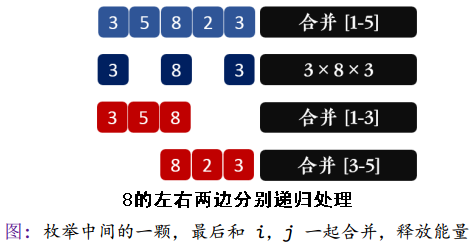
1 //T22:能量项链(DP) 2 int work(int *a)//对一段线性序列进行DP(枚举i~j合并起来,再枚举中间的k来合并) 3 { 4 for(int i=0;i<=n;++i) 5 for(int j=0;j<=n;++j) f[i][j]=0; 6 for(int s=2;s<=n;++s)//动态规划(从2开始——最少三个进行合并) 7 for(int i=0;i+s<=n;++i) 8 { 9 int j=i+s; 10 for(int k=i+1;k<j;++k)//枚举中间的一颗 11 f[i][j]=max(f[i][j],f[i][k]+f[k][j]+a[i]*a[k]*a[j]); 12 } 13 return f[0][n];//答案 14 }
经典例题:摆花(Luogu 1077)
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n 种花,从 1 到n 标号。为了在门口展出更多种花,规定第 i 种花不能超过 ai 盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
- 2 种花,要摆 4 盆
- 第一种花不超过 3 盆,第二种花不超过 2 盆
- 答案: 2
* 状态设计:设 F[i][j] 为摆到第 i 种花,共摆了 j 盆,的总方案数(枚举最后一种花摆了多少盆,往前推)
1 //T24:摆花(DP)时间复杂度:O(nm^2) 用前缀和可以优化为O(m) 2 f[0][0]=1; 3 for(int i=1;i<=n;++i) 4 for(int j=0;j<=m;++j) 5 for(int k=0;k<=j&&k<=a[i];++k) 6 f[i][j]=(f[i][j]+f[i-1][j-k])%MOD; 7 int ans=f[n][m];
经典例题:书本整理(Luogu 1103)
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉 k 本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有4 本书:
- 1x2 5x3 2x4 3x1 那么 Frank 将其排列整齐后是:
- 1x2 2x4 3x1 5x3 不整齐度就是 2+3+2=7
- 已知每本书的高度都不一样,请你求出去掉 k 本书后的最小的不整齐度。
* 第一步:先把书本按照高度排序!
* 状态设计:从 N 本书选出 N-k 本书;设 F[i][j] 为从前 i 本书选出j 本书的最小的不整齐度。
* 状态转移:讨论第 i 本书选不选?
* 上一种方法行不通!
- 为什么?我们需要计算选出相邻两本书之间的宽度的差的绝对值,而我们讨论第i本书选不选是算不出相邻两本书的不整齐度,因为你不知道上一本你选了哪本。
* 状态设计:从 N 本书选出 N-k 本书;设 F[i][j] 为从前 i 本书选出j 本书的最小的不整齐度,并且第 i 本书必须要选。
* 状态转移:上一本书选的是什么?
1 //T23:书本整理(DP) 2 int m=n-k;//共选出m本书 3 for(int i=1;i<=n;++i) 4 for(int j=1;j<=m;++j) 5 f[i][j]=INF;//初值 6 for(int i=1;i<=n;++i) f[i][1]=0;//初值,第一本书没有前一本,为0 7 for(int i=2;i<=n;++i) 8 for(int j=2;j<=m;++j) 9 for(int l=1;l<i;++l)//l为上一本书 10 f[i][j]=min(f[i][j],f[l][j-1]+abs(a[i]-a[l])); 11 int ans=INF; 12 for(int i=1;i<=n;++i) ans=min(ans,f[i][m]);//答案:最后一本书可以是任意一本
树形DP:
经典例题:奶牛家谱(Luogu 1472)
农民约翰准备购买一群新奶牛。在这个新的奶牛群中, 每一个母亲奶牛都生两个小奶牛。这些奶牛间的关系可以用二叉树来表示。这些二叉树总共有 N 个节点 (3 <= N < 200)。这些二叉树有如下性质:
每一个节点的度是 0 或 2。度是这个节点的孩子的数目。
树的高度等于 K(1 < K < 100)。高度是从根到最远的那个叶子所需要经过的结点数; 叶子是指没有孩子的节点。
有多少不同的家谱结构? 如果一个家谱的树结构不同于另一个的, 那么这两个家谱就是不同的。输出可能的家谱树的个数除以 9901 的余数。
- 5 个节点,高度为 3
- 答案:可能的家谱树个数为 2
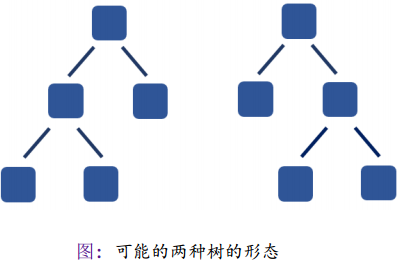
* 状态设计:看题说话(十分简单),设 F[i][j] 为 i 个节点高度为 j 的树,一共有多少种方案。
- 问题:如何进行状态转移?
- 分成左右两棵子树。
* 状态转移:枚举子树的状态
- 限制:注意要满足深度的限制
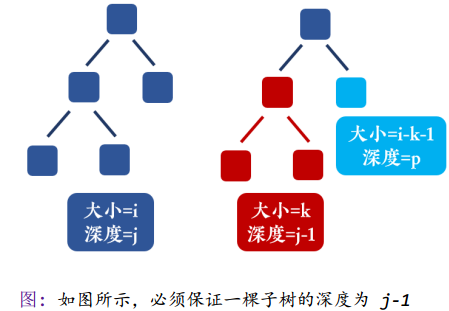
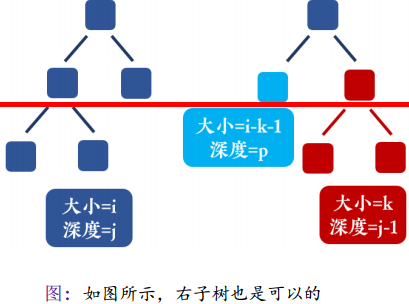
* 状态转移: F[i][j] = ∑ (k 为左子树大小, l 为右子树深度)+ F[k][j-1] * F[i-k-1][l] * 2 (l < j-1) (左右子树只有一棵深度为 j-1,直接翻倍)+ F[k][j-1] * F[i-k-1][j-1] (左右子树深度均为 j-1,不重复计算)
注意:在状态转移方程中:当我们左右子树的深度相同的话f[i][j] += f[k][j-1] * f[i-k-1][j-1] ,当左右子树深度不同的话我们可以截取到深度相同的部分,把下面所有往深度小的移(如上图右所示,把紫色树红线下方的子树全部移到右边去,变成红树),所以ans×2。
1 //T28:奶牛家谱(DP)时间复杂度:O(n^4) 2 f[1][1]=1;//初值,深度为1的子树只有一种情况 3 for(int i=3;i<=n;++i) 4 for(int j=2;j<=m;++j) 5 for(int k=1;k<i;++k) 6 { 7 for(int l=1;l<j-1;++l)//l<j-1,结果乘2 8 f[i][j]=(f[i][j]+f[k][j-1]*f[i-k-1][l]*2%MOD)%MOD;//左子树方案数*右子树方案数(乘法原理) 9 f[i][j]=(f[i][j]+f[k][j-1]*f[i-k-1][j-1]%MOD)%MOD;//左右子树深度相同,均为j-1 10 } 11 int ans=f[n][m];//答案以是任意一本
1 //T28:奶牛家谱(DP/前缀和优化)时间复杂度:O(n^3) 2 f[1][1]=g[1][1]=1; 3 for(int j=2;j<=m;++j) g[1][j]=1;//前缀和初始化 4 for(int i=3;i<=n;++i) 5 for(int j=2;j<=m;++j) 6 { 7 for(int k=1;k<i;++k)//注意到把深度小于j-1的方案全部加起来利用前缀和可以略去枚举过程 8 { 9 f[i][j]=(f[i][j]+f[k][j-1]*g[i-k-1][j-2]*2%MOD)%MOD; 10 f[i][j]=(f[i][j]+f[k][j-1]*f[i-k-1][j-1]%MOD)%MOD; 11 } 12 g[i][j]=(g[i][j-1]+f[i][j])%MOD;//前缀和计算 13 } 14 int ans=f[n][m];
经典例题:最大子树和(Luogu 1122)
一株奇怪的花卉,上面共连有 N 朵花,共有 N-1 条枝干将花儿连在一起,并且未修剪时每朵花都不是孤立的。每朵花都有一个“美丽指数”,该数越大说明这朵花越漂亮,也有“美丽指数”为负数的,说明这朵花看着都让人恶心。所谓“修剪”,意为:去掉其中的一条枝条,这样一株花就成了两株,扔掉其中一株。经过一系列“修剪“之后,还剩下最后一株花(也可能是一朵)。老师的任务就是:通过一系列“修剪”(也可以什么“修剪”都不进行),使剩下的那株(那朵)花卉上所有花朵的“美丽指数”之和最大。
* 样例如下图(红色树即为答案):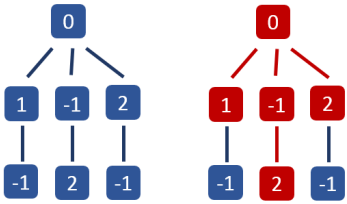
* 问题转化:在这棵树中取出若干个连通的节点,使得权值之和最大。
* 观察: 如下图,根节点为 0。假如我们必须要取根节点 0;同时它有三个儿子,权值分别为 2, 0, -3;则我们能取得的最大的权值是多少?
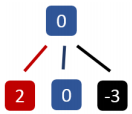
- 贪心地,我们只取不小于 0 的节点。(思路类似于求最大子段和)
* 算法思想: 贪心的只取不小于 0 的儿子。
* 状态设计:设 F[i] 为只考虑以 i 为根的这棵子树,并且必定要取 i 这个点,可能达到的最大权值是多少。
* 状态转移:把儿子中 F[x] 大于 0 的加起来即可。
1 //T29:最大子树和(DP) 2 void dfs(int x,int y=0)//y代表父亲节点(当传入参数是一个时,y默认为0,当传入两个参数,缺省参数y才会被修改) 3 { 4 f[x]=a[x];//x节点必取 5 for(unsigned i=0;i<e[x].size();++i) 6 { 7 int u=e[x][i]; 8 if(u==y) continue;//当u不为父亲节点 9 dfs(u,x);//递归求解儿子节点的f值 10 if(f[u]>=0) f[x]+=f[u];//当儿子权值大于0,则加上 11 } 12 }
1 //T29:最大子树和(DP) 2 //主程序 3 cin>>n; 4 for(int i=1;i<=n;++i) cin>>a[i]; 5 for(int i=1,x,y;i<n;++i) 6 { 7 cin>>x>>y;//树边 8 e[x].push_back(y);//增加树边 9 e[y].push_back(x);//增加树边 10 } 11 dfs(1);//递归求解f值 12 int ans=a[1]; 13 for(int i=1;i<=n;++i) ans=max(ans,f[i]);//答案取最大的一个 14 cout<<ans<<endl;
经典例题:选课(Luogu 2014)
在大学里每个学生,为了达到一定的学分,必须从很多课程里选择一些课程来学习,在课程里有些课程必须在某些课程之前学习,如高等数学总是在其它课程之前学习。现在有 N 门功课,每门课有个学分,每门课有一门或没有直接先修课(若课程 a 是课程 b 的先修课即只有学完了课程a,才能学习课程 b)。一个学生要从这些课程里选择 M 门课程学习,问他能获得的最大学分是多少?
* 下图所示:每个节点代表一节课;父亲代表他的先修课;红颜色代表选上的课。左边是一种合法的选课方式;而右边则是一种不合法的选课方式,2 的先修课 1 没有选上。
* 问题观察:我们可以观察得到,根节点的课一定是要选的;并且选的节点是和根节点联通的。 (否则不符合选课规则)
* 状态设计:设 F[i][j] 为,对于每节点 i,只考虑自己的子树,一共选了 j 节课,所能得到的最大权值是多少。假设i为根,并且包括i(根节点一定要选)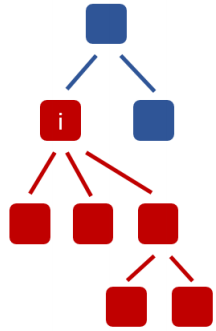
* 状态转移:假设 i 只有两棵子树,那么我们可以枚举在其中一棵子树中,我们一共选了几门课:
- F[i][j] = MAX (F[u][k] + F[v][j-k-1]) + A[i](意思是:我一定要选第i节课并且选了j节课的最优值A[i]+MAX(只考虑u这个节点并且u肯定是要选的,选了k节课的最优值,只考虑v这个节点并且v肯定是要选的,选了j-k-1节课的最优值))

* 状态转移:假设 i 有超过两棵子树,我们可以使用逐次合并的方法:先合并前两棵子树,然后将其视作一棵,再与余下的子树继续合并。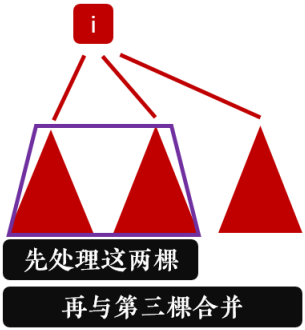
1 //T30:选课(DP)时间复杂度:nm^2 2 void dfs(int x)//处理根节点为x的子树 3 { 4 int *dp=f[x];//小技巧,用dp来代替f[x]数组 5 for(unsigned i=0;i<e[x].size();++i) 6 { 7 int u=e[x][i]; 8 dfs(u);//处理儿子节点的子树 9 //合并操作 10 //将已经合并的子树信息存放到dp数组当中 11 for(int j=0;j<=m;++j) tp[j]=0;//tp:临时数组 12 for(int j=0;j<=m;++j)//从已经合并的选j门 13 for(int k=0;j+k<=m;++k)//从新加入的u子树中选k门 14 tp[j+k]=max(tp[j+k],dp[j]+f[u][k]);//一共选了j+k节课选一个最大的->已经选了j门,要在新的子树中选k门 15 for(int j=0;j<=m;++j) dp[j]=tp[j];//复制过来(这样遍历完就是从所有子树中选j门课一共可以得到的学分最多是多少) 16 } 17 ... 18 }
1 //T30:选课(DP) 2 void dfs(int x)//处理根节点为x的子树 3 { 4 ... 5 //必须要选根节点这一门 6 for(int j=m;j;--j) dp[j]=dp[j-1]+a[x];//新的第j门=在众多子树中选了j-1门+当前 7 dp[0]=0; 8 }
1 //T30:选课(DP) 2 //主程序 3 cin>>n>>m,++m; 4 for(int i=1,fa;i<=n;++i) 5 cin>>fa>>a[i],e[fa].push_back(i); 6 //我们设所有没有先修课的父亲为0号 7 //这样结果是一样的,而且必须要选0号课程 8 dfs(0);//根节点出发,递归 9 cout<<f[0][m]<<endl;//在根节点多取m门课
状态压缩DP:
* 状态压缩 DP:利用位运算来记录状态,并实现动态规划。
* 问题特点:数据规模较小;不能使用简单的算法解决。
* 给定两个布尔变量a,b,他们之间可进行布尔运算:
* 与运算 and:当 a,b 均为真的时候, a 与 b为真;
* 或运算 or:当 a,b 均为假的时候, a 或 b为假;
* 非运算 not:当 a 均为真的时候, 非 a为假;
* 异或运算 xor:当 a,b 不是同时真,或者同时假的时候, a 异或 b为真。
* 我们把 0 视作布尔的假,1 视作布尔的真,则整数亦存在二进制的运算,而运算的结果则是二进制里对应的位作相应的布尔操作。(按位运算)
* (23)10 = (10111)2,(10)10 = (1010)2;
* 与运算 and: 23 and 10 = (10)2 = 2
* 或运算 or: 23 or 10 = (11111)2 = 31
* 异或运算 xor: 23 xor 10 = (11101)2 = 29
* 另外,在整数位运算中还有位移操作:
* (23)10 = (10111)2,(10)10 = (1010)2;
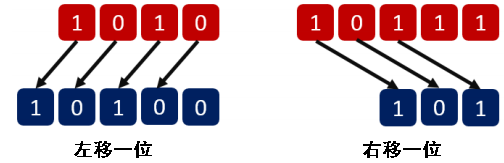
* 左移 «:将整个二进制向左移动若干位,并用 0 补充;
- 10 << 1 = (10100)2 = 20(左移n位=乘以2n)
* 右移 »:将整个二进制向右移动若干位(实际最右边的几位就消失了);
- 23 >> 2 = (101)2 = 5(右移n位=除以2n)
位运算比加减乘除都快!
经典例题:玉米田(Luogu 1879)
农场主 John 新买了一块长方形的新牧场,这块牧场被划分成 M 行 N列 (1 ≤ M ≤ 12; 1 ≤ N ≤ 12),每一格都是一块正方形的土地。 John打算在牧场上的某几格里种上美味的草,供他的奶牛们享用。
遗憾的是,有些土地相当贫瘠,不能用来种草。并且,奶牛们喜欢独占一块草地的感觉,于是 John 不会选择两块相邻的土地,也就是说,没有哪两块草地有公共边。
John 想知道,如果不考虑草地的总块数,那么,一共有多少种种植方案可供他选择?(当然,把新牧场完全荒废也是一种方案)
- 1 1 1
- 0 1 0 (1 代表这块土地适合种草)
- 总方案数: 9
* 问题限制:没有哪两块草地有公共边
* 考虑动态规划:如何划分状态?
- 从上到下,从左到右?
- 记录 F[i][j] 为 (i,j) 选择在这个位置种草的方案数?
- 问题:如何转移?我们只能限制左边的位置不能种草;不能限制上面的位置不能种草,所以这样不可行!
* 划分状态:考虑用行来划分状态; 第 i 行的状态只取决于第 i-1 行。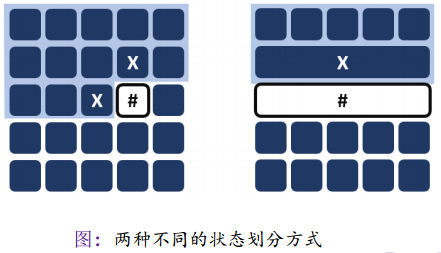
* 状态表示:如何表示一行的种草状态?
* 二进制位:将一整行看作是一个大的二进制数,其上为 1 表示种了草, 0表示没有种草,最好不用二维数组,因为行列数目不定,不好开数组。
* 这样,我们可以用一个数来表示一行的种草状态;
例如:下图中,在一行的第一个位置和第四个位置种草,可以用18来表示这种状态:
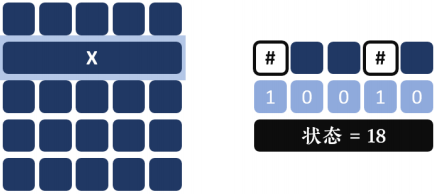
* 状态设计:设 F[i][j] 为已经处理到第 i 行,且第 i 行的状态是 j,的总方案数。 (其中 j 为一个大的二进制数)
* 状态转移:枚举前一行的种草状态 k,如果没有产生冲突,则加上:
F[i][j] = ∑ F[i − 1][k]
* 问题:如何判断两个状态是否冲突? 如何运用二进制运算?

* 解决方案:采取与运算;如果两个状态是冲突的,则肯定有一位上都为1, and 的结果肯定不为 0;否则若结果为 0,则代表状态不冲突。
* 下一个问题:如何判断当前状态j是合法的?
1 没有占有障碍物:和判断两个状态是否冲突是类似的。
2 左右位置判断:与上一行判断冲突,我们只考虑到了上下位置不可能同时种草,但还没有考虑左右的情况。
- 解决方案: j & (j«1) = 0 且 j & (j»1) = 0(我只想说:左右两个相互叠加判断,真TM聪明!)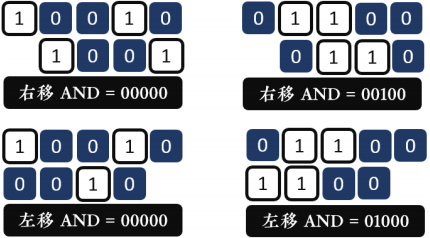
1 //T31:玉米田(状态压缩DP) 2 const int N=13;//边长 3 const int S=(1<<N)+5;//二进制状态数=213,+5的目的是让心里有个安慰~应该不会爆炸吧O(∩_∩)O,开大点数组这样 4 int a[N][N];//棋盘数组 5 int s[N];//每一行空地的状态 6 int f[N][S];//动态规划数组 7 int g[S];//标记一个状态是否合法 8 //主过程 9 ts=1<<m;//总状态数 10 for(int i=0;i<ts;++i)//判断左右位置 11 g[i]=((i&(i<<1))==0)&&((i&(i>>1))==0);//左右位置是否有冲突
1 //T31:玉米田(状态压缩DP) 2 f[0][0]=1;//初值! 3 for(int i=1;i<=n;++i)//枚举行 4 for(int j=0;j<ts;++j)//枚举这行的状态 5 if(g[j]&&((j&s[i])==j))//状态本身合法且不占障碍物 6 { 7 for(int k=0;k<ts;++k)//枚举上一行的状态 8 if((k&j)==0)//如果不冲突 9 f[i][j]=(f[i][j]+f[i-1][k])%MOD; 10 } 11 int ans=0; 12 for(int j=0;j<ts;++j) 13 ans=(ans+f[n][j])%MOD;//答案加起来
1 //T31:玉米田(状态压缩DP) 2 cin>>n>>m;//读入棋盘状态 3 for(int i=1;i<=n;++i) 4 for(int j=1;j<=m;++j) 5 cin>>a[i][j]; 6 for(int i=1;i<=n;++i)//预处理每一行的状态 7 for(int j=1;j<=m;++j) 8 s[i]=(s[i]<<1)+a[i][j];
经典例题:互不侵犯(Luogu 1896)
* 在 N×N 的棋盘里面放 K 个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共 8 个格子。
- 3 2 (在 3×3 的棋盘内放置 2 个国王)
- 总方案数: 16
* 状态设计:设 F[i][j][k] 为已经处理到第 i 行,且第 i 行的状态是j,现在一共放置了 k 个国王的总方案数。 (其中 j 为一个大的二进制数)
* 状态转移:枚举前一行的放置国王状态为 l,如果没有产生冲突,则加上(其中 x 为状态 j 的国王数)
F[i][j][k] = ∑ F[i − 1][l][k − x]
* 问题:如何判断两个状态是否冲突? 如何运用二进制运算?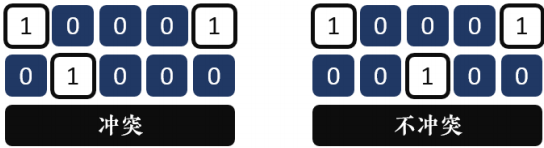
1 //T32:互不侵犯(状态压缩DP) 2 const int N=10; 3 const int S=(1<<N)+5;//二进制状态数 4 int cnt[S];//记录一个状态有多少个1(按照这个状态放国王,一共有多少个国王) 5 int g[S];//记录一个状态是否合法 6 int h[S]; 7 LL f[N][S][N*N];//动态转移状态->[行][状态][一共摆了多少个国王]
1 //T32:互不侵犯(状态压缩DP) 2 ts=1<<n; 3 for(int i=0;i<ts;++i) 4 { 5 g[i]=((i&(i<<1))==0)&&((i&(i>>1))==0); 6 h[i]=i|(i<<1)|(i>>1);//h:一个状态把它左右都占据之后的状态(h[i]表示第i个国王把他左右旁边占领之后,标记为1) 7 cnt[i]=cnt[i>>1]+(i&1);//计算多少个1((i&1)表示最后一个是1就++) 8 }
1 //T32:互不侵犯(状态压缩DP) 2 f[0][0][0]=1;//初值 3 //顺推 4 for(int i=0;i<n;++i)//行数 5 for(int j=0;j<ts;++j)//这一行状态 6 for(int l=0;l<=k;++l) if(f[i][j][l])//枚举个数 7 for(int p=0;p<ts;++p)//枚举下一行 8 if(g[p]&&((h[p]&j)==0))//如果是合法状态,且不冲突(p是一个合法状态,p国王占的领地和j是没有冲突的) 9 { 10 f[i+1][p][l+cnt[p]]+=f[i][j][l]; 11 } 12 LL ans=0;//答案 13 for(int j=0;j<ts;++j) ans+=f[n][j][k];//所有的状态都能成为答案
经典例题:Little Pony and Harmony Chest(Codeforces 453B)
* 我们称一个正整数序列 B 是和谐的,当且仅当它们两两互质。
- 给出一个序列 A,求出一个和谐的序列 B,使得∑ |Ai − Bi| 最小。
* 问题思考:一个和谐的序列两两互质,满足什么性质?
- 它们分解质因数后,没有两个数拥有相同的质因子。
* 状态构思:如果我已经决定完前 i 个数是多少,现在要决定下一个数,需要满足什么限制?——不能有和前面重复的质因子。
- 这代表我们需要记录下,目前已经用了哪些质因子了。
* 状态设计:设 F[i][j] 为,已经决定完前 i 个数是多少,而且已经用了状态为 j 的质因子了,现在的最小权值差是多少。
- 如何状态压缩? 2,3,5,7,11,...;一个代表一个二进制位;用了是 1,没有是 0。
1 //T35:CF453B(状态压缩DP) 2 cin>>n; 3 for(int i=1;i<=n;++i) cin>>a[i]; 4 for(int i=2;i<M;++i)//预处理质数(筛法) 5 { 6 if(!fg[i]) p[++p[0]]=i; 7 for(int j=1;j<=p[0]&&i*p[j]<M;++j) 8 fg[i*p[j]]=1; 9 } 10 for(int i=1;i<M;++i)//预处理每个数的质因子所代表的状态 11 { 12 g[i]=0; 13 for(int j=1;j<=p[0];++j)//如果i是这个质因子的倍数 14 if(i%p[j]==0) 15 { 16 g[i]|=1<<(j-1);//因为是从1到j-1的,第一个质因子是1,第二个质因子是2,第三个4,第四个8…这样就能得到每一个数它拥有哪些质因子的情况 17 } 18 }
1 //T35:CF453B(状态压缩DP) 2 //动态规划主过程 3 int ns=1<<p[0]; 4 //初值:最大值(因为要求最小值) 5 for(int i=1;i<=n+1;++i) 6 for(int j=0;j<ns;++j) f[i][j]=S; 7 f[1][0]=0; 8 for(int i=1;i<=n;++i)//枚举位置 9 for(int j=0;j<ns;++j) if(f[i][j]<S)//枚举状态 10 for(int k=1;k<M;++k)//枚举这个位置的数 11 if((g[k]&j)==0)//g[k]:第k个数,拥有哪些质因子的状态,如果之前没有出现过(两个状态没有冲突,没有出现重复的质因子,执行) 12 { 13 //计算最优值 14 int t=f[i][j]+absp(k-a[i]); 15 if(t<f[i+1][g[k]|j])//更新最优值 16 f[i+1][g[k]|j]=t, 17 opt[i+1][g[k]|j]=k;//opt:取到最优值时,选最后一个数是什么 18 }
1 //T35:CF453B(状态压缩DP) 2 //最优值输出 3 int ansp=S; 4 int ansm=0; 5 for(int j=0;j<ns;++j)//记录最优值所对应的状态 6 if(f[n+1][j]<ansp) ansp=f[n+1][j],ansm=j;//ansp:最优值,ansm:最优状态 7 for(int i=n+1;i>1;--i)//依次向前查询,逆推 8 { 9 b[i-1]=opt[i][ansm]; 10 ansm^=g[b[i-1]];//相当于减去 11 } 12 for(int i=1;i<=n;++i) cout<<b[i]<<" "; 13 cout<<endl;
经典例题:愤怒的小鸟(Luogu 2831)NOIP2016提高组
Kiana最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于(0,0)处,每次Kiana可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如的曲线,其中a,b是Kiana指定的参数,且必须满足a<0。
当小鸟落回地面(即x轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有n只绿色的小猪,其中第i只小猪所在的坐标为(xi,yi)。
如果某只小鸟的飞行轨迹经过了(xi,yi),那么第i只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过(xi,yi),那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。
例如,若两只小猪分别位于(1,3)和(3,3),Kiana可以选择发射一只飞行轨迹为的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有T个关卡,现在Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
【输入】
第一行包含一个正整数T,表示游戏的关卡总数。
下面依次输入这T个关卡的信息。每个关卡第一行包含两个非负整数n,m,分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的n行中,第i行包含两个正实数(xi,yi),表示第i只小猪坐标为(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果m=0,表示Kiana输入了一个没有任何作用的指令。
如果m=1,则这个关卡将会满足:至多用只小鸟即可消灭所有小猪。
如果m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少只小猪。
保证1<=n<=18,0<=m<=2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号和
分别表示对x向上取整和向下取整
【输出】
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量
* 状态设计:能设计形如 F[i],表示前 i 只小猪都打下来的最小的小鸟数吗?
- 无法这样做。我一次可以打下若干只小猪,而且没有顺序之分
* 状态设计:用一个大的二进制数 s 表示哪些小猪被打下来了(1 表示打下来了, 0 表示没有打下来)。设 F[s] 为打下状态为 s 的小猪, 最小的小鸟数。
* 状态转移:采用顺推。考虑下一步我们可以打下状态为 t 的小猪,则可以这样更新:
F[s or t] = MIN (F[s or t], F[s] + 1)(F[s]表示用了多少小鸟,+1表示这个状态多用了一只小鸟),用F[s]+1的小鸟打下F[s or t]的小猪。
- s or t 表示我现在一共打下了 s 和 t 状态的小猪。
1 //T33:愤怒的小鸟(状态压缩DP) 2 //DP主过程 3 int ns=1<<n; 4 for(int i=1;i<ns;i++) dp[i]=n;//初值,最多就n只小鸟 5 for(int i=0;i<ns;i++) 6 { 7 int l=(ns-1)^i;//异^或操作;选出没有打下的小猪 8 l=mk[l&(-l)];//l表示第一只没被打下的小猪 9 for(int j=1;j<=g[l][0];j++)//选择一种打的方式 10 { 11 dp[i|g[l][j]]=min(dp[i|g[l][j]],dp[i]+1);//g[l][j]为能够打到的小猪的状态 12 } 13 } 14 printf("%d ",dp[ns-1]);//答案
总结状压DP:
* 状态压缩 DP:用一个二进制数来记录状态
* 特点:记录一些东西是否出现过
* 难点:位运算判断;状态的设计
* 标志:数据范围不大,某一个状态特别小
最近发现一些网站盗用我的blog,这实在不能忍(™把关于我的名字什么的全部删去只保留文本啥意思。。)!!希望各位转载引用时请注明出处,谢谢配合噢~