数的计算——递归与函数自调用算法

题目描述 Description

　　我们要求找出具有下列性质数的个数(包含输入的自然数n):
　　先输入一个自然数n(n<=1000),然后对此自然数按照如下方法进行处理:
　　1.不作任何处理;
　　2.在它的左边加上一个自然数,但该自然数不能超过原数的一半;
　　3.加上数后,继续按此规则进行处理,直到不能再加自然数为止.

 输入输出格式 Input/output

输入格式：
一个自然数n(n<=1000)
输出格式：
一个整数，表示具有该性质数的个数。

 输入输出样例 Sample input/output

样例测试点#1

输入样例：

6

输出样例：

6

思路：

方法一：

用递归，f(n)=1+f(1)+f(2)+…+f(div/2)，当n较大时会超时，时间应该为指数级。

 

方法二：用记忆化搜索，实际上是对方法一的改进。设h[i]表示自然数i满足题意三个条件的数的个数。如果用递归求解，会重复来求一些子问题。例如在求h[4]时，需要再求h[1]和h[2]的值。现在我们用h数组记录在记忆求解过程中得出的所有子问题的解，当遇到重叠子问题时，直接使用前面记忆的结果。

 

方法三：

用递推，用h(n)表示自然数n所能扩展的数据个数，则h(1)=1, h(2)=2, h(3)=2, h(4)=4, h(5)=4, h(6)=6, h(7)=6, h(8)=10, h(9)=10.分析以上数据，可得递推公式：h(i)=1+h(1)+h(2)+…+h(i/2)。此算法的时间度为O(n*n)。

设h[i]-i按照规则扩展出的自然数个数(1≤i≤n)。下表列出了h[i]值及其方案：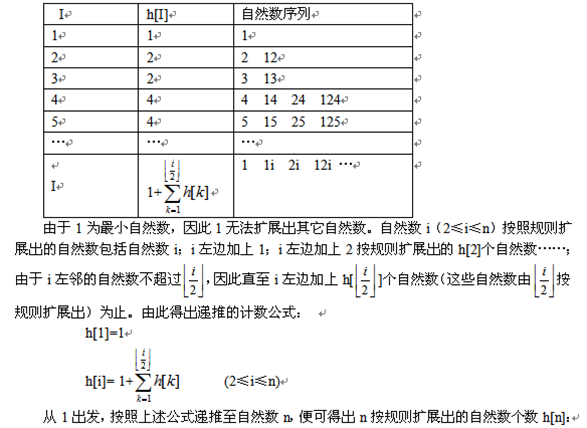

 

方法四：

w是对方法三的改进，我们定义数组s，s(x)=h(1)+h(2)+…+h(x),h(x)=s(x)-s(x-1)，此算法的时间复杂度可降到O(n)。

 

方法五：

w还是用递推，只要作仔细分析，其实我们还可以得到以下的递推公式: (1)当i为奇数时，h(i)=h(i-1);

w     (2)当i为偶数时,h(i)=h(i-1)+h(i/2).

 

代码①如下（递归）：

#include<stdio.h>
int ans;
void dfs(int m)                           //统计m所扩展出的数据个数
{
    int i;
    ans++;                                  //每出现一个原数，累加器加1；
    for (i = 1; i <= m/2; i++)         //左边添加不超过原数一半的自然数，作为新原数
    dfs(i); 
}
int main()
{
    int n;
    scanf("%d",&n);
    dfs(n);
    printf("%d
",ans);
    return 0;
}

代码②如下（非递归）：

#include <stdio.h>    
int main()    
{    
    int a[1001]={0};   
    int n,p;
    scanf("%d",&n);  
    a[1]=1;  
    a[2]=2;    
    for(p=3;p<=n;p++)
    {
        if(p%2==1) 
        {
            a[p]=a[p-1];   
        }
        else 
        {
            a[p]=a[p-1]+a[p/2];    
        }                  
    } 
    printf("%d
",a[n]);
    return 0;    
}