数据结构----------双向链表

数据结构之双向链表

　　双向链表区别于单向链表的地方在于：前后两个节点是双向关联的，即可通过前一个节点的next指针域访问后一个节点，由后一个节点的prev域访问前一个节点，其逻辑结构图如下所示：

　　

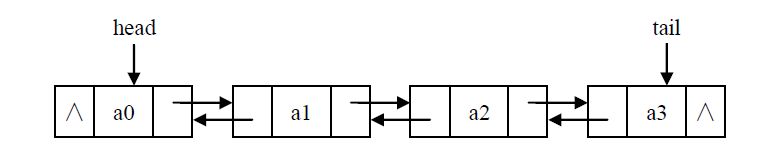
　　在这里，头结点和尾节点均为空节点（其节点中存储的数据为null），可在吗构造方法将数据初始化为null。

　　话不多说，直接 从代码出发!

•  API

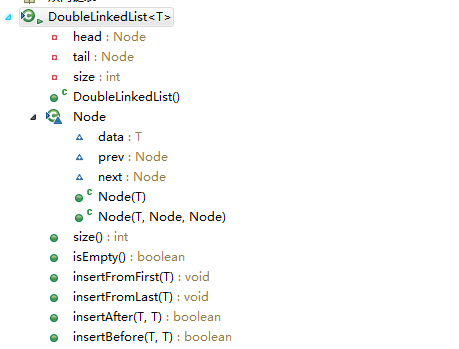• 实现

public class DoubleLinkedList<T> {
    private Node head;//头结点
    private Node tail;//尾节点
    private int size;//链表中节点数量（不包括头节点和尾节点）
    
    
    public DoubleLinkedList() {
        this.head = new Node(null); //头节点和尾节点并不存储数据
        this.tail = new Node(null);
    }

    /**
     * 链表节点类
     * @author Administrator
     *
     */
    class Node {
        T data;//数据
        Node prev;//前一个节点
        Node next;//后一个节点
        
        public Node(T data) {this.data = data;};
        public Node(T data, Node prev, Node next) {
            this.data = data;
            this.prev = prev;
            this.next = next;
        }
    }
    
    /**
     * 返回链表长度
     * @return
     */
    public int size() {
        return size;
    }
    
    /**
     * 判断链表是否为空
     * @return
     */
    public boolean isEmpty() {
        return size == 0;
    }
    
    /**
     * 从链表头部添加节点
     * @param data
     */
    public void insertFromFirst(T data) {
        Node newNode = new Node(data);
        if(isEmpty()) {//如果链表为空
            head.next = newNode;
            tail.prev = newNode;
        }else {//如果链表不为空
            newNode.next = head.next;
            head.next.prev = newNode;
            head.next = newNode;
        }
        size++;
    }
    
    /**
     * 
     * 从链表尾部添加节点
     * @param data
     */
    public void insertFromLast(T data) {
        Node newNode = new Node(data);
        if(isEmpty()) {//如果链表为空
            head.next = newNode;
            tail.prev = newNode;
        }else {//如果链表不为空
            tail.prev.next = newNode;
            newNode.prev = tail.prev;
            tail.prev = newNode;
        }
        size++;
    }
    
    /**
     * 在匹配节点后添加新的节点：添加成功返回true，反之，返回false
     * @param data 新节点数据
     * @param key  要匹配的节点
     * @return
     */
    public boolean insertAfter(T data, T key) {
        if(isEmpty()) {//链表为空，返回false;
            return false;
        }
        Node current = head.next;
        while(null != current) {
            if(key.equals(current.data)) {//找到匹配的key,在其后添加新节点
                Node newNode = new Node(data);
                newNode.next = current.next;
                current.next.prev = newNode;
                current.next = newNode;
                newNode.prev = current;
                size++;
                return true;
            }
            current = current.next;
        }
        return false;//没有找到匹配的key，返回false
    }
    
    /**
     * 在匹配节点后添加新的节点
     * @param data 新节点数据
     * @param key  要匹配的节点
     * @return
     */
    public boolean insertBefore(T data, T key) {
        if(isEmpty()) {//链表为空，返回false;
            return false;
        }
        Node current = head.next;
        while(null != current) {
            if(key.equals(current.data)) {//找到匹配的key,在其前添加新节点
                Node newNode = new Node(data);
                newNode.prev = current.prev;
                current.prev.next = newNode;
                newNode.next = current;
                current.prev = newNode;
                size++;
                return true;
            }
            current = current.next;
        }
        return false;//没有找到匹配的key，返回false
    }
    
    /**
     * 从头节点遍历数据
     */
    public void printFromFirst() {
        if(isEmpty()) return;
        Node current = head.next;
        int i = 0;
        while(null != current) {
            System.out.println("this is the" + (i++) + "th node: data = " + current.data);
            current = current.next;
        }
    }
    
    /**
     * 从链表尾部遍历数据
     */
    public void printFromLast() {
        if(isEmpty()) return;
        Node current = tail.prev;
        int i = size();
        while(null != current) {
            System.out.println("this is the" + (--i) + "th node: data = " + current.data);
            current = current.prev;
        }
    }
    
    /**
     * 从链表头部删除元素，返回被删除节点
     * @return
     */
    public Node deleteFromFirst() {
        if(isEmpty()) return null;
        
        Node deleteNode = head.next;
        head.next.next.prev = null;
        head.next = head.next.next;
        size--;
        return deleteNode;
    }
    
    /**
     * 从尾部删除节点 返回被删除节点 
     * @return
     */
    public Node deleteFromLast() {
        if(isEmpty()) return null;
        Node deleteNode = tail.prev;
        tail.prev.prev.next = null;
        tail.prev = tail.prev.prev;
        size--;
        return deleteNode;
    }
    
    /**
     * 删除与制定数据匹配的节点，如果没有返回null
     * @param data
     * @return
     */
    public Node deleteNode(T data) {
        if(isEmpty()) return null;
        Node current = head.next;
        while(null != current) {
            if(data.equals(current.data)) {
                current.prev.next = current.next;
                current.next.prev = current.prev;
                size--;
                return current;
            }
            current = current.next;
        }
        return null;
    }
    
}