机器人学 —— 估计和学习-第一周

第一周 you learned about how to use Gaussian Models to estimate and learn from uncertain data. 

第二周 we saw how to track these distributions over time in week two using the Kalman Filter. 

第三周, you learn about robotic mapping and how to represent uncertainty in the objects in the environment around the robot. 

第四周, you learn how robots can keep track of their pose over time, using a particle filter for localization

1.1 Introduction

1.2 Single Dimensional Gaussian

1.2.1 1D Gaussian Distribution

yellow ball example: 使用高斯模型来描述HSV空间的H通道中，某个像素是否属于黄色球的概率。

Advantage：only use two parameters instead of all pixels in the image

Question: How to estimate two parameters in gaussian model?

1.2.2 Maximum Likelihood Estimate of Gaussian Model Parameters

Answer:  How to estimate two parameters in gaussian model?

The derivation process of the MLE for univariate gaussian in supplementary

1.3 Multivariate Gaussian

1.3.1 Multivariate Gaussian Distribution

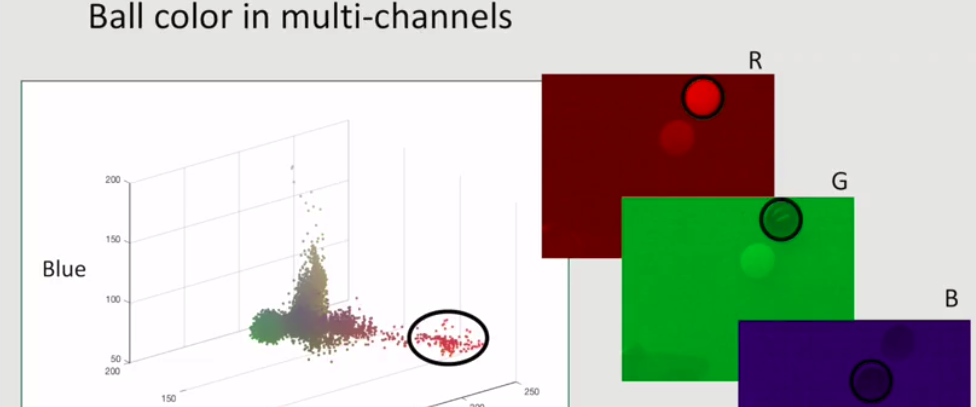
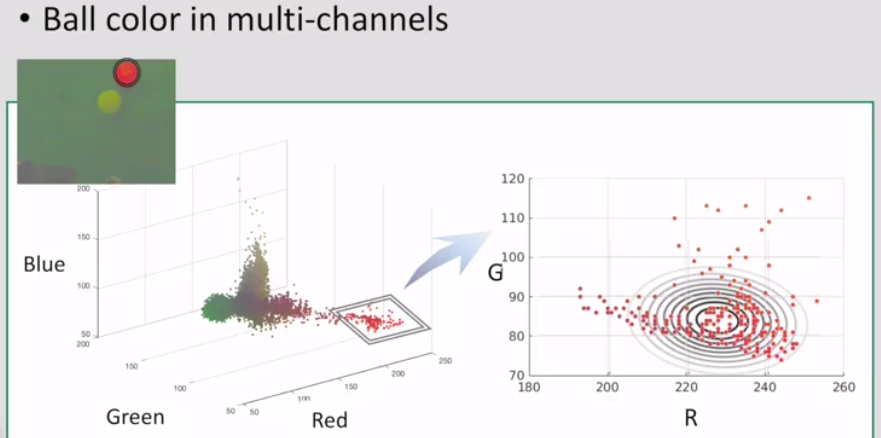
red ball example: 使用多变量高斯模型描述RGB空间中，某个像素是否属于红色球的概率。

Multivariate Gaussian

 

sigma is a square matrix;

|sigma| ： determinant of sigma

_{^{The correlation component represents how much one variable is related to another one.}}

1) Positive Definite: all eigenvalues of sigma must be positive;

2) We can always find the coordinate transformation which makes the shape appear symmetric even when the covariance matrix has none zero correlation terms.

How to model the red ball example?

Q: How to estimate parameters of the multivariate gaussian model?

 1.3.2 MLE of Multivariate Gaussian

Answer: How to estimate parameters of the multivariate gaussian model.

The derivation process of the MLE for multivariate gaussian in supplementary

 

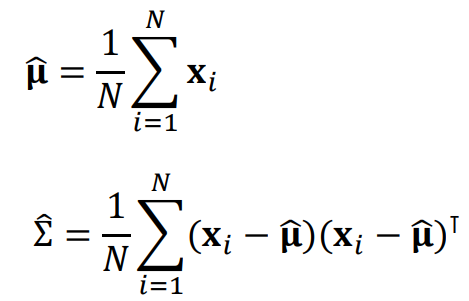
 come back to the color ball example:

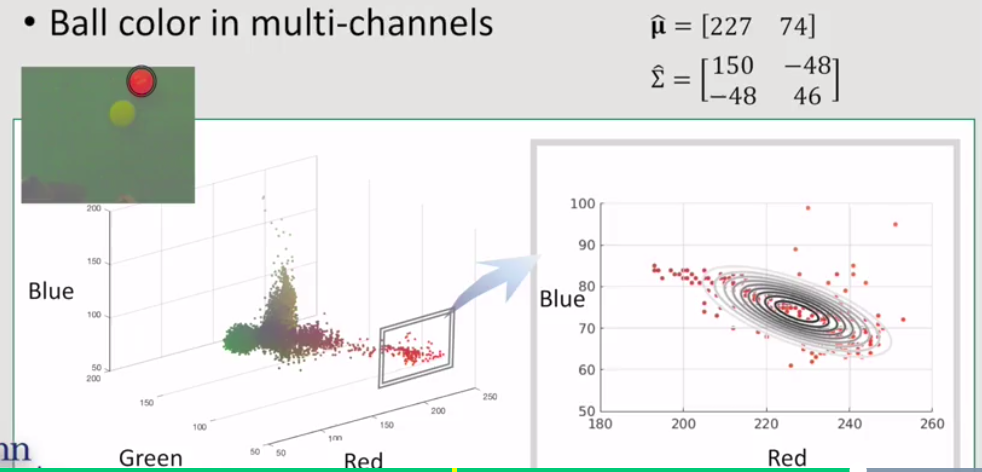
From the contours in the plot, we can check that the red and blue channel are correlated negatively in the model.

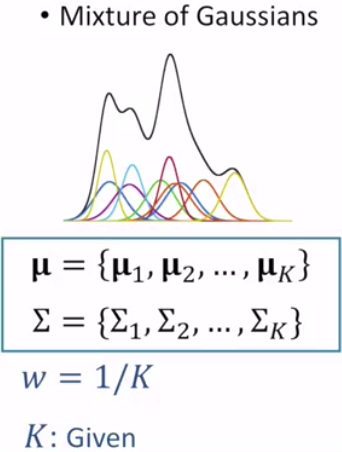
1.4 Mixture of Gaussian

1.4.1 Gaussian Mixture Model(GMM)

Limitations of Single Gaussian

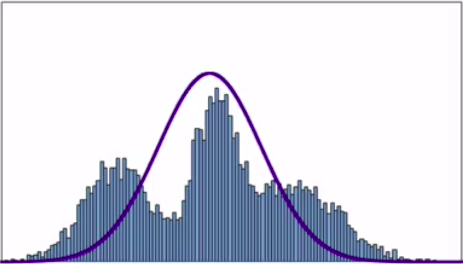
Description, black line is the GMM.

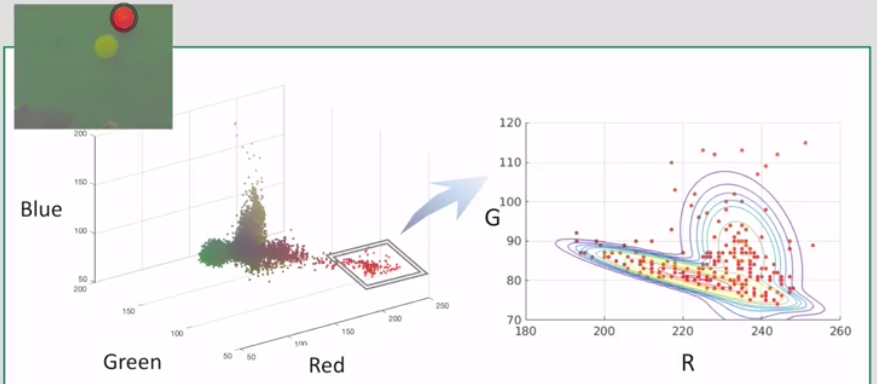
red ball example

Try to use 2D gaussian model to represent values in R and G channels.

Try to use GMM to represent values in R and G channels

Mathematics model

The sum of w_k is 1, which ensure the integral of GMM is 1.

Three disadvantages:

1) more parameters;

2) No analytic solution

3) overfitting

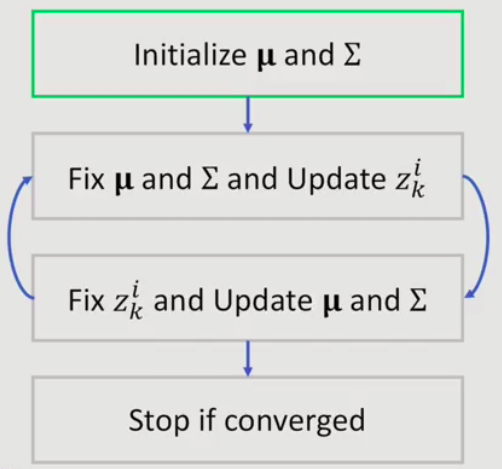
1.4.2 GMM Parameter Estimation via EM

 

w = 1/k, to simplify the deduction process.

Let's begin to find the maximum likelihood estimate of GMM parameters 

more detail about deduction plz refer to supplementary

EM for GMM

    

    

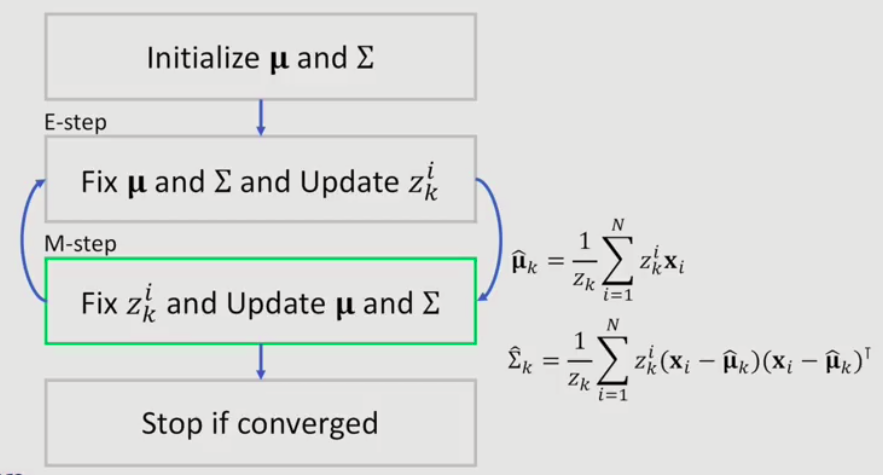
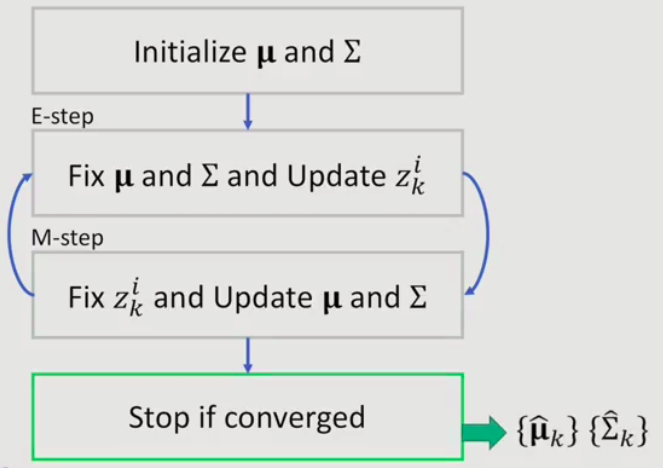
1.4.3 Expectation-Maxization(EM)

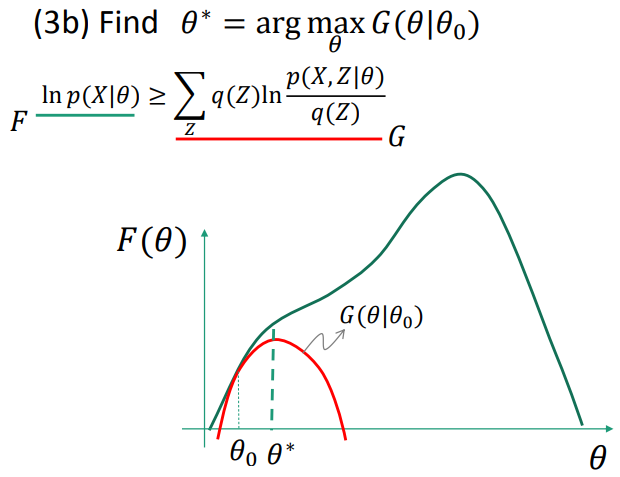
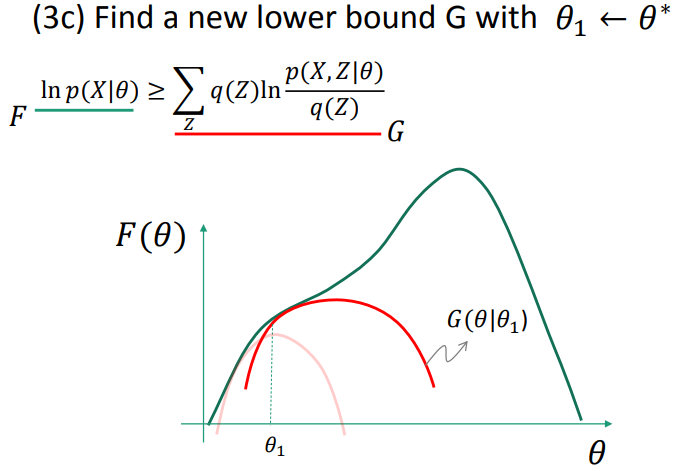
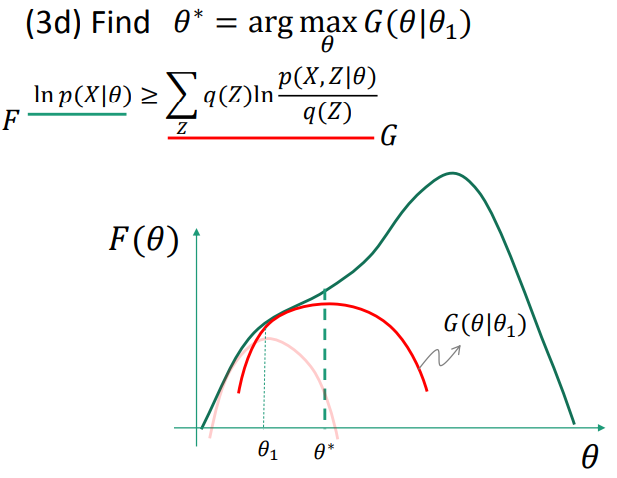
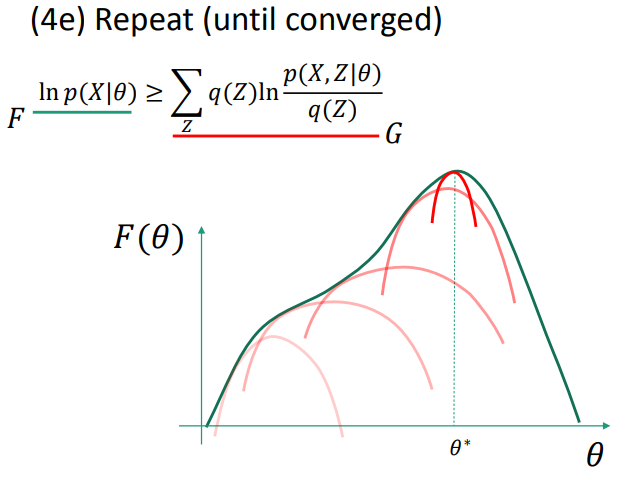
EM as lower-bound maximization

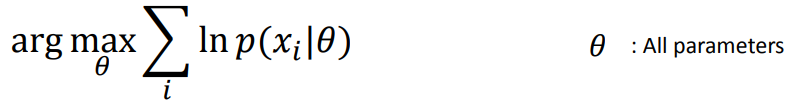
introduce 3 concepts:

(1) Jensen's inequality(详见课程ppt)

如ppt中所定义，ln对数函数是凹函数，积分的函数值大于函数的积分值。

 

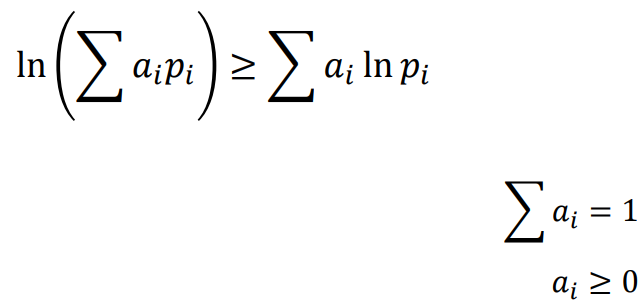
(2) Latent variable and marginal probability

引入潜在变量Z。Z的来源参见GMM。

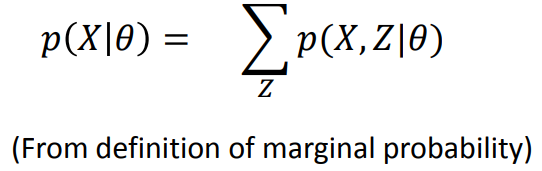
找出Z的分布q，从而确定极大似然估计的lower bound。

(3) procedure : E-step and M-step(详见课程ppt)