图的最优化问题:最小生成树、最短路径
典型的图应用问题
无向连通加权图的最小生成树
有向/无向加权图的最短路径
四个经典算法
Kruskal算法、Prim算法---------------最小生成树
Dijkstra算法、Floyd算法-------------最短路径
最小生成树的概念:
G=(V,E):无向连通加权图
C(e)或C(v,w): 边e=(v,w)的耗费(Cost)
若S=(V,T)是G的一棵生成树(T是树边集),那么, S的边长之和称作生成树S的耗费C(S)
耗费C(S)达到最小值的生成树S,称为G的最小耗费生成树,也称最小生成树(MinimumSpanningTree)
即C(S)≤C(S') (S'是图G的任一生成树)
注意:最小生成树可能不唯一
Kruskal算法
算法思想: 按长度从小到大的依次把边加进生成树,若添加某边后形成了回路,就舍弃这条边
反复如此,直到选出n-1条边,便得到最小生成树.。
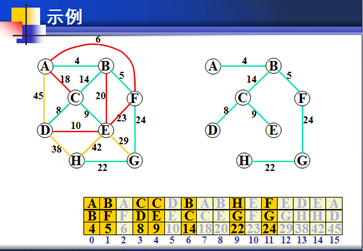
通俗来讲,该算法很简单。
步骤:
1.在空白处画出与原图一模一样的结点位置。(只画结点,权不需要,结点的位置要一模一样)。
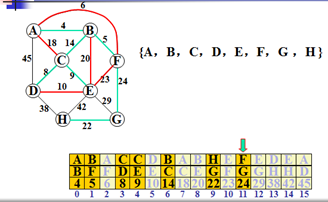
2.按权画边。从权值最小的开始,如图,从4开始,草图就连A-B,到权值5,就连B-F,到权值6,此时就会发现,如果连接A-F,那么A-B-F就会构成一个完整的回路(从任意一点出发可以回到原点。)。因此,就要舍去权值6,即边A-F不可连接。。。。。依次按权大小画其他边。直到最后一个结点。
Kruskal算法伪程序形式
void Kruskal(***) //***表示函数要求的参数
{ int et=0; //et用于记录选中的边数
置树边集T为空;
while(et<n-1) //n是图中的顶点数
{ 从G中选出当前最短边(v,w);
if(添此边于T中,不使生成树产生回路)
{ 把(v,w)加进T;et++;}
else 舍弃(v,w);
}
}
实现方法分析:
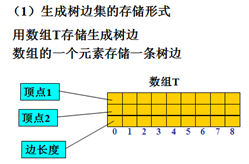
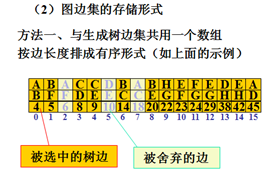


子树合并法描述和示例

描述:
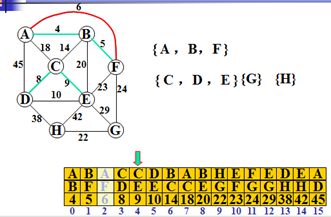

Kruskal算法的子树合并法描述形式:
方法一:
void Kruskal(***) //***表示函数要求的参数
{ int et=0;
每个顶点自成一个集合,并指定集合名;
while(et<n-1)
{ 从G中选出当前最短边(v,w);
找到v所在的集合名i,和w所在的集合名j;
if(i!=j)
{ 把(v,w)加进T; et++;
将集合i与集合j合并成一个集合k; }
}
}
方法二:
void Kruskal(***) //***表示函数要求的参数
{ int et=0;
每个顶点一个集合,并指定集合名 ;
while(et<n-1)
{ 从G中选出当前最短边(v,w);
if(v和w不在同一子树中)
{ 把(v,w)加进T;et++;
将v所在的子树与w所在的子树合并成一棵子树;
}
}
}
结论:无论是按权画边法,还是子树合并法都是可以找出最小生成树,但是个人认为按权画边法比较容易理解。