一、什么是图灵机?
图灵机(Turing machine),是艾伦・麦席森・图灵(1912-1954年)于1936年提出的一种抽象的计算模型,即将人们使用纸笔进行数学运算的过程进行抽象,由一个虚拟的机器替代人类进行复杂的数学运算。它有一条无限长的纸带,纸带分成了一个一个的小方格,每个方格有不同的颜色。有一个机器头在纸带上移来移去。机器头有一组内部状态,还有一些固定的程序。在每个时刻,机器头都要从当前纸带上读入一个方格信息,然后结合自己的内部状态查找程序表,根据程序输出信息到纸带方格上,并转换自己的内部状态,然后进行移动。其实就是现代计算机原理的雏形。
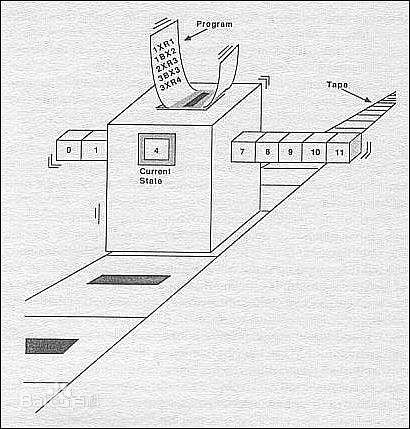
图灵机可以做下面三个基本的操作:
- 读取指针头指向的符号。
- 修改方框中的字符。
- 将纸带向左或向右移动,以便修改其临近方框的值。
简单例子,我们将在空白的纸带条上打印1 1 0这三个数字:
1.首先,我们向head指向的方框中写入数字1:

2.接着,我们让纸带向左移动一个方框:

3.我们再往指针头指向的方框写入数字1:

4.最后,我们继续让纸带向左移动一个方框,并写入数字0:

理论上可以用图灵机完成各种复杂的运算,只要提前设计好各种策略指令输入给图灵机,把策略表中的信息以统一的格式写成符号串,然后放在纸带的头部,再设计一台能在运行伊始时从纸带上读取这些策略的图灵机,那么针对不同的任务,就不需要设计不同的图灵机,而只需改变纸带上的策略即可,这其实就类似于现在的编程,所以说是早期计算机的雏形。这种能靠纸带定制策略的图灵机,称为通用图灵机UTM(universal Turing machine)
图灵机在当时带来的深远意义
让我们尝试这样的思考历程:
- 我有许多很复杂的公式需要计算,如果自己一个人算的话时间会很久。
- 思考:能不能有一个东西能帮我实现公式的计算,无论这个公式有多复杂?
- 思考:我能不能设计一个模型来证实这个实行是可行的?(数学家最喜欢建模型来证明了~)
- 思考:提出「图灵机」理论,任何计算都可以简化成固定的步骤,无论多复杂的计算都能实现了。
- 某些动手能力强的数学家利用电子工程学知识将许多真空管组成了一套设备,实现了「图灵机」理论模型。
- 随着电子工程的不断发展,原本庞大的计算机不断变小,慢慢地变成了今天的计算机。
「图灵机」理论通过假设模型证明了任意复杂的计算都能通过一个个简单的操作完成,从而从理论上证明了「无限复杂计算」的可能性,直接给计算机的诞生提供了理论基础。从这样的思考历程来看,图灵机的出现为计算机的诞生奠定了理论基础,这就是图灵机诞生的意义。
二、什么是图灵测试?
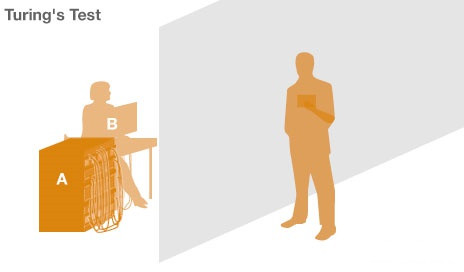
将人与机器隔开,前者通过一些装置(如键盘)向后者随意提问。多次问答后,如果有超过30%的人不能确定出被测试者是人还是机器,那么这台机器就通过了测试,并被认为具有人类智能。
一个是正常思维的人(代号B)、一个是机器(代号A)。如果经过若干询问以后,C不能得出实质的区别来分辨A与B的不同,则此机器A通过图灵测试。
三、什么是图灵完备性?
在可计算性理论里,如果一系列操作数据的规则(如指令集、编程语言、细胞自动机)可以用来模拟单带图灵机,那么它是图灵完备的。如今主流的编程语言(c++,java,python等)都是图灵完备的语言,其语言优劣之争无非就是在封装、优化方面。如果回到最底层,它们可以实现的功能其实完全一样,并且本质上就是一个图灵机。
四、神经图灵机(Neural Turing Machine)
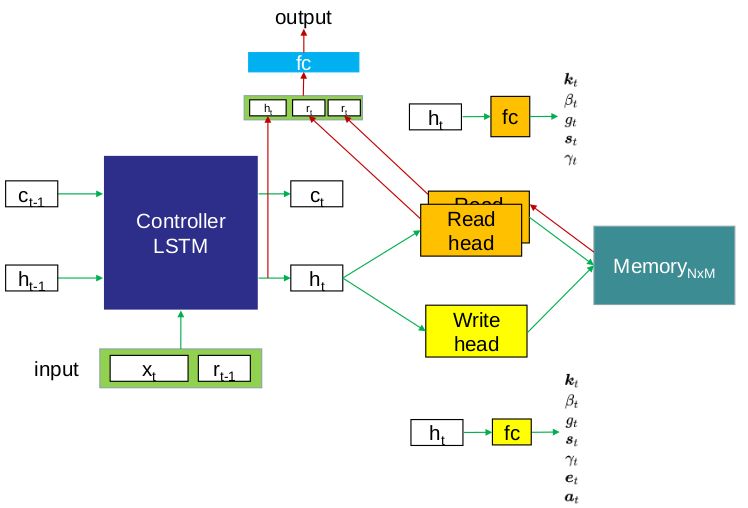
神经图灵机(NTM)简而言之就是一种神经网络,但它是从图灵机中获得灵感来尝试执行一些计算机可以解决得很好而机器学习模型并不能很好地解决的任务。它主要由三部分组成:Controller(控制器)、Head(读写指针头)、Memory(外部存储器)。
①Controller控制器是一个神经网络,用于提供输入的内部表示,通过读写头与存储器相互作用。值得注意的是,这种内部表征与最终储存在存储器中的并不完全相等,后者是这种表征的一种转换。对于神经网络机来说,控制器的类型就是最重要架构选择的代表。这种控制器可以是前馈或递归神经网络。前馈控制器比起一个递归控制器要快速得多,并提供更多的透明度。但这意味着付出低表现力的代价,因为它限制了NTM每时间步所能执行的计算类型。
②Head读写指针头让神经网络图灵机更加有趣,它们是仅有的能够直接与存储器互动的成分。从内部来说,每个读写头的行为都被它自身的权重向量所控制,在每一时间步得到刷新。每个向量上的权重分布与在记忆中的位置一致(权重向量总和为1),利用注意力机制实现NTM的聚焦,NTM所关注的位置权重最大且尽可能会接近1,反之则接近0.
五、利用论文中的Copy实例说明NTM的工作原理
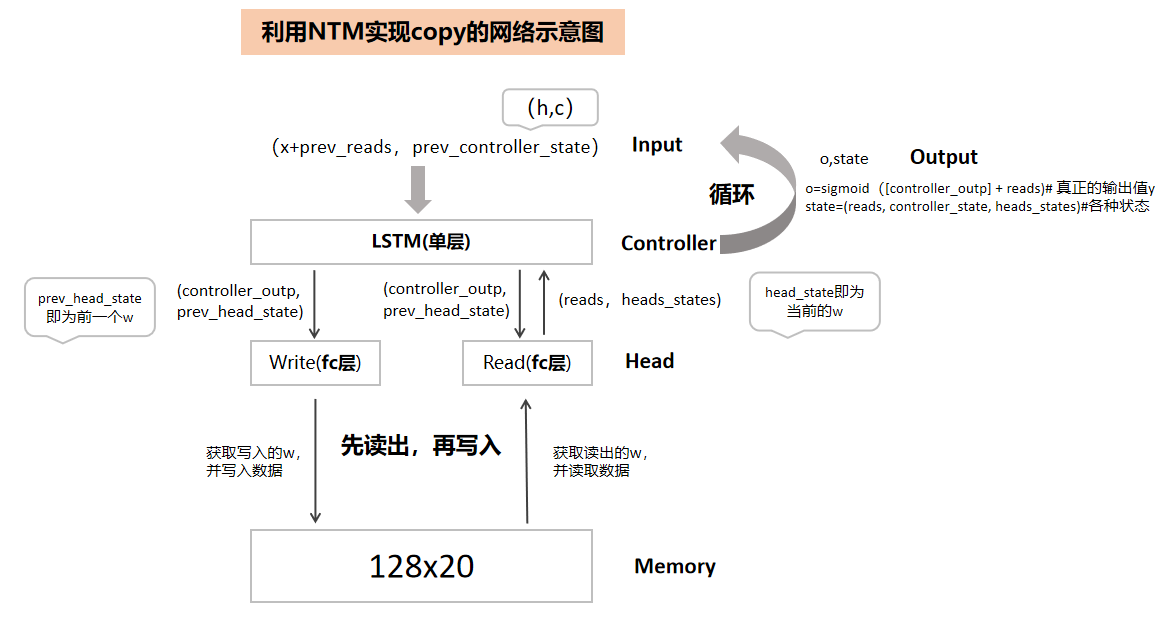
NTM有两个指针头,一个读指针头Head,一个写指针头Head。Copy实例中Controller是1个单层的LSTM,读写各1个Head,每次都是先执行ReadHead,然后再是WriteHead。
![]()
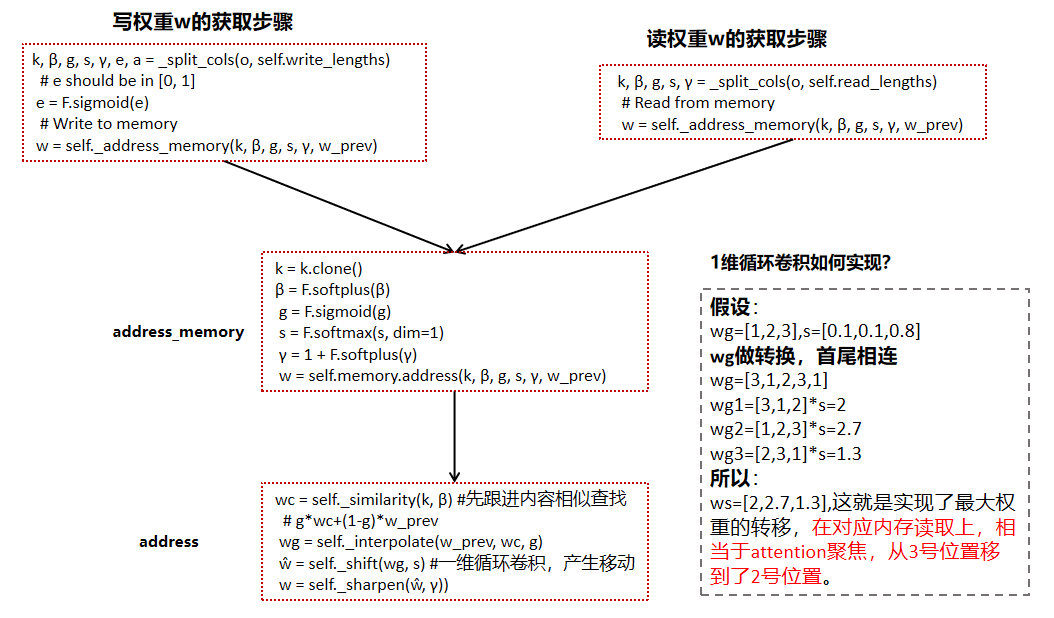
Copy实例的训练过程如下:
先执行数据写入Memory阶段:
1.根据输入的seq_len,遍历输入x
2.x和前一个read的内容拼接一起,及LSTM的前一个h和c的输出,共同作为本次LSTM的输入
3.LSTM输出out,h和c,其中out和head的前一个权重输出w共同作为本次head的输入。
4.然后就先执行ReadHead,再执行WriteHead,在此阶段主要写为主,读操作无实际意义。
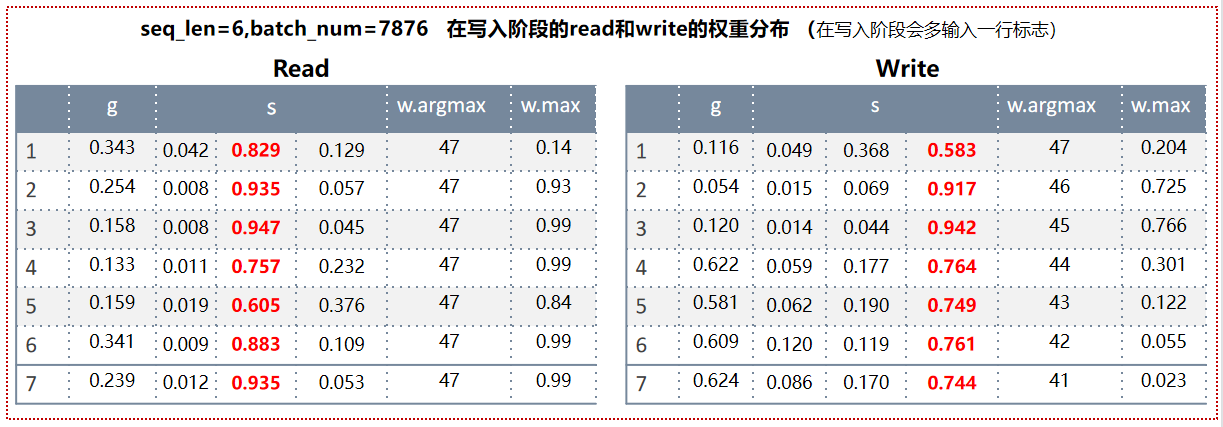
权重分析:
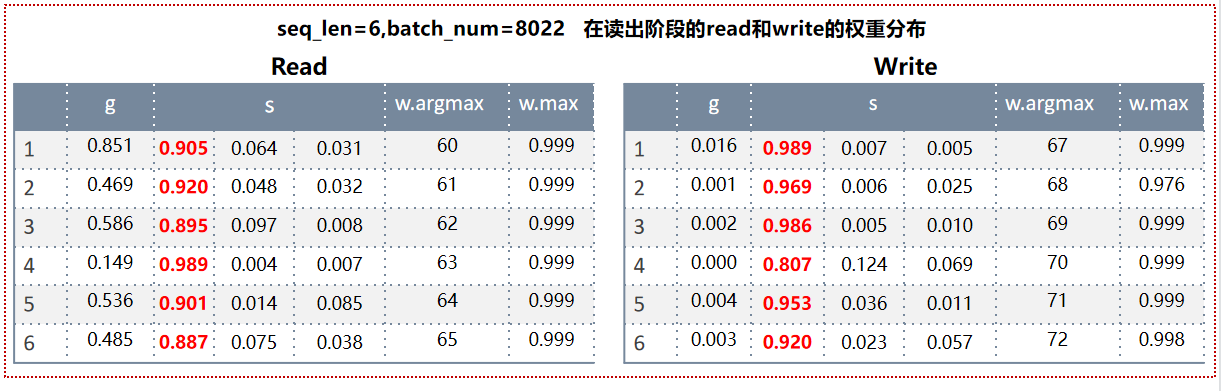
在数据写入阶段,虽然有读也有写,但此时主要是要写入数据,读操作其实没有意义,所以可以看到Read的g都<0.5,也就是这一步更新w主要以上一步w值为主;然后到shift操作阶段,开始1维循环卷积,左边代表上面的权重,中间的代表自己的权重,右边代表自己下面位置的权重,可以看到自己的权重值远远大于上下的,所以Read的位置始终保持不变,而且自己权重的值非常大。而Write的shift阶段中,都是其下面的权重最大,这样当前的最新权重大多来自于其上一次下面的权重值,就会导致WriteHead从下向上不断上移指针,而根据argmax能看到,也确实如此,写入内存的编号越来越小。
再执行数据的读出阶段:
1.根据输出的seq_len开始进行遍历,此时没有输入数据,所以输入x都为zeros
2.x和前一个read的内容拼接一起,及LSTM的前一个h和c的输出,共同作为本次LSTM的输入
3.LSTM输出out,h和c,其中out和head的前一个权重输出w共同作为本次head的输入。
4.依然是先执行ReadHead,再执行WriteHead,在此阶段主要以读出为主,写操作无实际意义

权重分析:
可以看到此时的Read的权重分布和第一阶段的Write的权重分布比较相似了,其原理同上;而此时Write权重分布就跟第一阶段的Read相似,原理也同上。
反向传播,优化模型:
读出来的y_out 和实际的y计算loss,开始反向传播,优化模型,通过dataloader不断随机输出迭代数据循环上述两个阶段,每次的输出seq_len都是1~20之间,因为是copy机制,所以x和y其实是一个值,就是写入一个seq长的数据,再读出同样seq长的数据,且数据一模一样,就完成训练了,大概迭代输入7000次左右模型就训练ok了。
六、调整目标值Y的学习
Copy机制是输入X是什么,读出来的Y就是什么,一模一样,现在换个思路,让NTM学习输入的下一个位置内容,比如输入X=[[1,0,1],[1,1,0],[0,0,1]],学习的Y分别后移一位,Y=[[1,1,0],[0,0,1],[1,0,1]]。经过模型迭代训练,依然能够很好的学习到,可以通过两个阶段的变化来看其学习的过程:
执行数据写入Memory阶段:
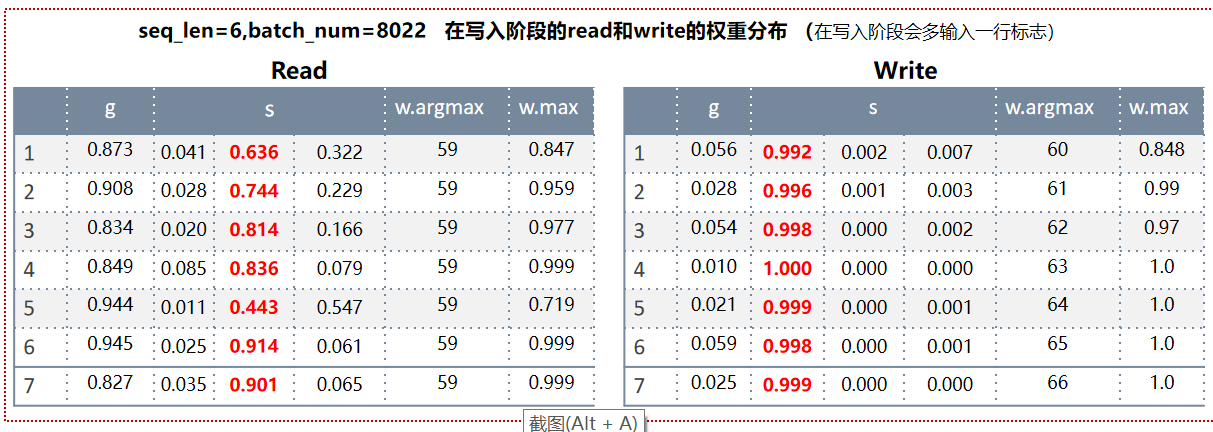
执行数据读出Memory阶段: