二叉排序树

一、定义

二叉排序树（Binary Sort Tree）又称二叉查找树、二叉搜索树。 它或者是一棵空树；或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

首先实现二叉排序树的搜索，因为后续无论对二叉排序树进行增加、删除都要先进行查找。

def bst_search(btree,key):
    bt=btree
    while bt is not None:
    　　if key==bt.value:
        　　return True
        elif key>bt.value:
            bt=bt.right
        else:
            bt=bt.left
    return False     

 如果二叉树的结构良好，其高度与树中结点个数n成对数关系，检索的时间开销为O(logn)，但是如果树结构为畸形，检索的最坏时间可能达到O(n),如下图的树：

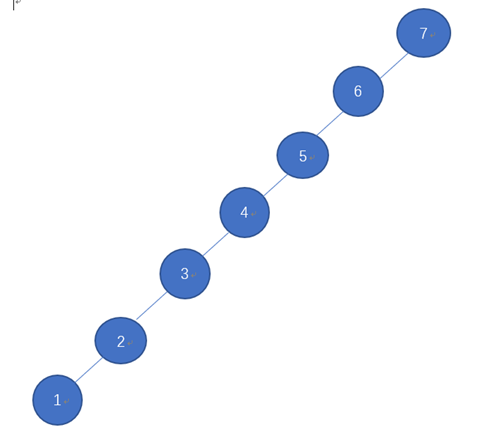
但是如果是下面这样的结构，则平均检索时间就能达到O(logn)：

从上述两棵树而已看出，一组有序数据，是可以构建多种不同的二叉排序树，但是哪种才是最优的二叉排序树呢？从上可以看出第二颗树明显优于第一个，第二个树正是平衡二叉排序树，所以平衡二叉排序树才是最优的。

二、平衡二叉排序树(AVL树)

 平衡二叉排序树，又叫AVL树，是由它们的发明者苏联人的名字命名的，定义如下：

平衡二叉排序树是一类特殊的二叉排序树，它或者为空树，或者其左右子树都是平衡二叉排序树，而且其左右的子数高度之差绝对值不超过1.

AVL树的查找平均复杂度是O（log(n)）。

 在每一次树插入新元素后，树的平衡都可能被破坏，需要旋转调整树的高度，以达到平衡树结构，共分为以下四种情况：

• LL：对该结点的左儿子的左子树进行了一次插入，需右旋转
• LR：对该结点的左儿子的右子树进行了一次插入，先左后右
• RL：对该结点的右儿子的左子树进行了一次插入，先右后左
• RR：对该结点的右儿子的右子树进行了一次插入，需左旋转

旋转原则：在旋转的时候，都是要以离新插入节点最近的不平衡子树进行旋转，注意旋转的这部分子树一定是不平衡的子树。

1）LL情况

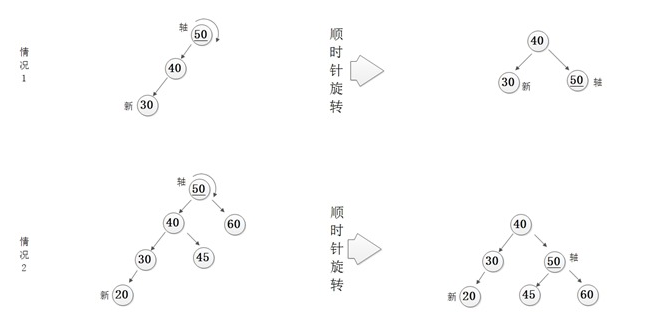
2）RR情况

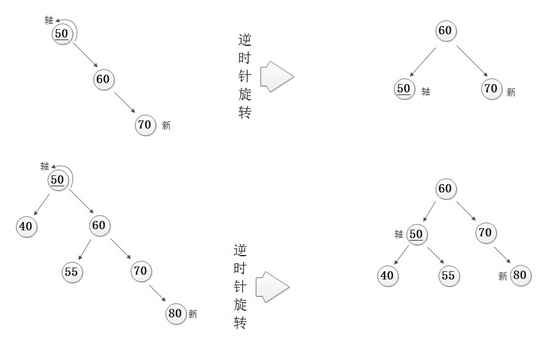
3）LR情况

4）RL情况

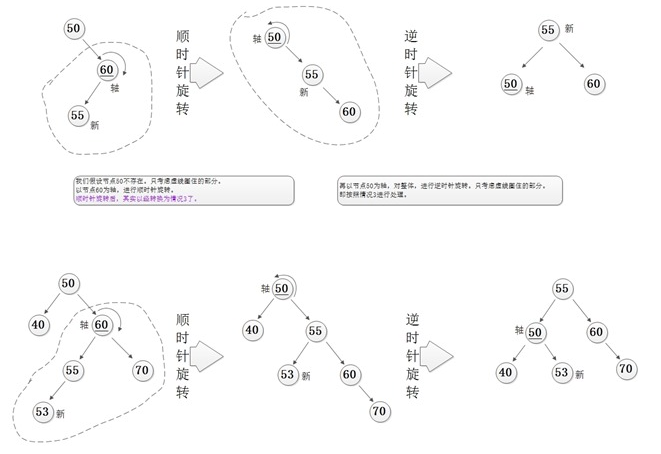
 python代码实现参考：https://www.cnblogs.com/linxiyue/p/3659448.html?utm_source=tuicool&utm_medium=referral